Доказательства равных треугольников: как доказать равенство углов, 3 признака равенства, подобие треугольников

Как установить и доказать, что треугольники равны

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

∠ α = ∠ β исходя из построения фигур.
Дано в условии задания.
При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
Всегда сходны вертикальные ∠ α и ∠ β
Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH . делит ∠ α на два равнозначных.
Смежный с ∠90° — угол, равный исходному.
Смежные равным углам равны.
Высота образует два смежных ∠90° .
В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , => треугольники равны.
III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

Первый — о двух соответственно равных углах двух рассматриваемых треугольных фигур.
Второй — об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
Третий — указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

Подобие и равенство треугольников

В данном уроке мы сформулируем и докажем три признака равенства треугольников, а также три признака подобия треугольников.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока “Подобие и равенство треугольников”

· поговорить о равенстве и подобии треугольников;

· сформулировать и доказать три признака равенства треугольников;

· сформулировать и доказать три признака подобия треугольников.

Напомним, что две фигуры называют равными, если их можно совместить.

Давайте, возьмём два равных треугольника и . И наложим их друг на друга.

Видим, они совместились, то есть попарно совместились их вершины и стороны. А значит, попарно совместились и углы этих треугольников.

Следовательно, можем сделать вывод: если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.

Также следует отметить, что в равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот: против соответственно равных углов лежат равные стороны.

Равенство треугольников и обозначают следующим образом:

И говорят «треугольник А Б Ц равен треугольнику А₁ Б₁ Ц₁».

Исходя из рассмотренного, можно сказать, что равенство треугольников мы можем установить не только наложением их друг на друга, но и сравнивая их элементы.

Для установления равенства треугольников пользуются соответствующими признаками равенства треугольников.

Итак, первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

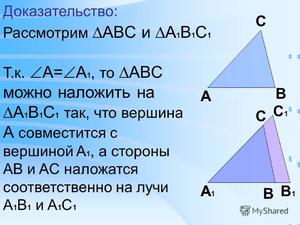
Докажем это утверждение. Пусть и – треугольники, у которых , , . Докажем, что .

Так как , то совместится с , а и совместятся с лучами и .

Так как , а , то совместится с , а – с . Исходя из этого, точка совместится с , – с . Следовательно, совместится с .

Тогда имеем, треугольники и полностью совместились. Значит, .

Таким образом, теорема доказана.

На рисунке , . Доказать, что .

Рассмотрим два треугольника и . У них стороны равны по условию задачи. Выше мы выяснили, что , а угол – общий угол. Следовательно, данные треугольники равны по первому признаку равенства треугольников. Значит, у них соответственные стороны и углы равны. То есть . Что и требовалось доказать.

Сформулируем второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Докажем это утверждение. Пусть и – треугольники, у которых , , . Докажем, что .

Совместим треугольник с треугольником 1 таким образом, чтобы вершина А совместилась с вершиной А₁, сторона АВ – с равной ей стороной А₁В₁, а вершины С и С₁ оказались по одну сторону от прямой А₁В₁.

Так как и , то совместится с , а – с . Поэтому вершина С – общая точка сторон АС и ВС, окажется лежащей и на лучах А₁С₁ и В₁С₁, а следовательно, совместится с общей точкой этих лучей – вершиной С₁. Значит, совместятся стороны и , и . Получаем, что треугольники и полностью совместятся. А значит, .

Отрезки и пересекаются в точке , которая является серединой отрезка , а . Доказать, что .

Рассмотрим и . У них , так как Е – середина отрезка АВ. Углы равны по условию задачи. А углы равны как вертикальные. Получаем, что треугольники равны по второму признаку.

Прежде чем сформулировать третий признак равенства треугольников, давайте немного подробнее поговорим о равнобедренных треугольниках.

Напомним, что треугольник называется равнобедренным, если две его стороны равны.

Возьмём, к примеру, треугольник , у которого стороны . Как мы уже отмечали, эти стороны называют боковыми сторонами. Третья сторона называется основанием равнобедренного треугольника. Точка называется вершиной равнобедренного треугольника, а точки и – вершинами при его основании. Угол называется углом при вершине, а углы и – углами при основании.

Теперь сформулируем некоторые теоремы о свойствах равнобедренного треугольника.

Первая теорема звучит следующим образом: в равнобедренном треугольнике углы при основании равны.

И вторая теорема: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Ну а теперь давайте перейдём к третьему признаку равенства треугольников.

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Докажем это утверждение. Пусть и – два треугольника, у которых , , . Докажем, что .

Приложим треугольник к треугольнику таким образом, чтобы вершина А совместилась с вершиной А₁, вершина В – с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой А₁В₁. Тогда возможны три случая.

Рассмотрим первый случай.

Так как по условию теоремы , , то треугольники и являются равнобедренными. По теореме о свойстве углов равнобедренного треугольника , . Поэтому .

Итак мы знаем, что , и . Следовательно, треугольник по первому признаку равенства треугольников.

Рассмотрим второй случай.

Так как по условию теоремы , то треугольник является равнобедренным. По теореме о свойстве углов равнобедренного треугольника углы при основании . Можем сказать, что треугольники по первому признаку равенства треугольников, так как , , .

И третий случай.

По условию теоремы и . Из этого следует, что треугольники и являются равнобедренными. Тогда по теореме о свойстве углов при основании равнобедренного треугольника . А, следовательно, . Итак, треугольники по первому признаку равенства треугольников, так как и по условию теоремы, а .

Отрезок – общее основание равнобедренных и. Докажите, что .

Доказательство. Рассмотрим треугольники и . У этих треугольников , , а сторона – общая. Тогда получаем, что треугольники по третьему признаку равенства треугольников.

Что и требовалось доказать.

Теперь перейдём к признакам подобия треугольников.

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Подобные треугольники обозначают следующим образом: .

Сформулируем первый признак подобия треугольников.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть у треугольников и , .

Напомним, что сумма углов треугольника равна 180 о . Значит, для наших треугольников можем записать следующие равенства:

Выразим из первого равенства , а из второго – угол . Так как по условию , , то, следовательно, . То есть у рассматриваемых треугольников углы соответственно равны.

Теперь докажем, что сходственные стороны этих треугольников пропорциональны.

Так как , то по теореме: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы; площадь треугольника .

Углы , а тогда отношение площадей наших треугольников равно .

Заметим, что у этих равенств левые части одинаковые, а тогда можно приравнять их правые части:

Упростим, получившееся равенство. Для этого обе части равенства разделим на , а затем умножим на . И получим,

Аналогично, так как , , то имеют место следующие равенства:

Их левые части равны, а тогда можем приравнять их правые части. Упростим, получившееся равенство. И получим,

Таким образом, из полученных равенств следует .

То есть мы получили, что сходственные стороны треугольников и пропорциональны. Выше мы доказали, что соответственные углы этих треугольников равны, а значит, .

Что и требовалось доказать.

На рисунке: см, см, см, а . Найти .

Рассмотрим треугольники и . У них углы по условию задачи, а – общий. Значит, по первому признаку.

Из подобия треугольников следует пропорциональность их сходственных сторон: . Подставим известные значения сторон из условия задачи: . Выразим . Запишем ответ.

Сформулируем и докажем второй признак подобия треугольников.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Рассмотрим треугольники и , у которых , .

Построим на стороне треугольника треугольник , у которого , . Тогда треугольники по первому признаку. Для сходственных сторон можем записать, что .

По условию, . А тогда их этих двух равенств получим, что .

Рассмотрим треугольники и . У них . Сторона – общая. , так как и . А значит, треугольники по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников.

Таким образом, мы получили, что треугольник , а построенный треугольник . Отсюда следует, что треугольник .

Что и требовалось доказать.

На одной из сторон отложены отрезки и , равные соответственно см и см. На другой стороне этого же угла отложены отрезки и , соответственно равные см и см. Подобны ли и ?

Рассмотрим треугольники и . У них – общий. Составим отношения сторон , , образующих . Видим, что эти отношения равны, а значит, .

А, следовательно, треугольники по двум сторонам и углу между ними, то есть по второму признаку подобия треугольников.

Ну а теперь сформулируем третий признак подобия треугольников.

Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство. Рассмотрим треугольники и , у которых стороны соответственно пропорциональны .

Построим на стороне треугольника треугольник , у которого , .

Тогда треугольники по первому признаку подобия треугольников. Поэтому стороны .

По условию стороны . Сравнивания эти равенства, получаем, что ; .

Тогда треугольники по третьему признаку равенства треугольников, так как только что мы получили, что ; , а сторона у них общая. Следовательно, у этих треугольников углы соответственно равны, то есть . А так как , то .

Таким образом, мы получаем, что у треугольников и стороны пропорциональны и . Следовательно, по второму признаку подобия треугольников.

Что и требовалось доказать.

Выяснить, подобны ли и , если см, см, см, см, см, см?

Так как нам известны длины всех сторон данных треугольников, то проверим, пропорциональны ли стороны треугольника сторонам треугольника .

Найдём отношения сторон:

Видим, что эти отношения равны, а значит, . Следовательно, по третьему признаку подобия треугольников.

На этом уроке мы говорили о равенстве и подобии треугольников. Сформулировали и доказали три признака равенства треугольников. А также сформулировали и доказали три признака подобия треугольников.

Признаки равенства треугольников

Если две стороны и угол между ними, одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника,, то такие треугольники равны. Доказательство. Пусть даны треугольники и , у которых и (рис. 2.1). Докажем, .

Так как то треугольник можно наложить на треугольник так, что вершина совпадает с вершиной , а лучи и с лучами и соответственно. По аксиоме VIII о существовании треугольника, равного данному, такое наложение возможно единственным образом. Так как , то сторона совпадает со стороной а сторона – со стороной , т.е. точки и , и совпадут. Следовательно, совпадут стороны и . Итак, треугольники и полностью совпадут. Значит, они равны. Теорема доказана. Доказанная теорема выражает признак (равенство треугольников по двум сторонам и углу между ними), по которому можно сделать вывод о равенстве треугольников.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Второй признак равенства треугольников

Теорема 2. (Признак равенства треугольников по стороне и прилежащим к ней углам.)

Если сторона и прилежащие к ней углы, одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника то такие треугольники равны. Доказательство. Пусть даны треугольники и , у которых и (рис. 2.2). Докажем, что . Так как , то треугольник можно наложить на треугольник так, что вершина совпадет с вершиной , а луч совпадет с лучом и вершина будет находиться в той же полуплоскости, что и вершина по отношению к прямой . Так как , то вершина совпадет с вершиной . Поскольку , то луч совпадет с лучом и луч совпадет с лучом . Отсюда следует, что вершина совпадет с вершиной . Итак, треугольники и совпадают, т.е. . Теорема доказана.

Возможно вам будут полезны данные страницы:

Пример с решением №1

Отрезки и пересекаются в точке , которая является серединой каждого из них. Чему равен отрезок , если Решение:

Так как (как вертикальные) и (т.к. точка – середина и ), то по I признаку равенства треугольников . Поэтому (рис. 2.3).

Высота, биссектриса, медиана, средний линия треугольника

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр,проведенный из этой вершины к прямой, проходящей через противоположную сторону треугольника. На рисунке 2.17 основание высоты лежит на стороне , а на рисунке 2.18 основание высоты лежит на продолжении стороны треугольника .

Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. На рисунке 2.19 – биссектриса. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежающей стороны треугольника. На рисунке 2.20 – медиана.

Средней, линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2.20 – средняя линия.

Свойства равнобедренного треугольника. Понятие обратная теорема

Треугольник называется paвнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника. На рисунке 2.21 изображен равнобедренный треугольник , в котором – боковые стороны, – основание. Треугольник, у которого все стороны равны, называется равносторонним. На рисунке 2.22 изображен равносторонний треугольник , в котором .

Теорема 3.

В равнобедренном треугольнике биссектриса, проведенная к основанию, является и медианой, и высотой. Доказательство. Пусть отрезок является биссектрисой равнобедренного треугольника , проведенной к его основанию (рис. 2.23). Нужно показать, что является и медианой, и высотой треугольника . Действительно, так как является биссектрисой, то , а так как — равнобедренный, то . К тому же отрезок является общей стороной треугольников и . Тогда (по первому признаку равенства треугольников). Поэтому , т.е. является медианой и (как равные смежные углы), т.е. . Следовательно, является и высотой. Теорема доказана.

Теорема 4.

1) В равнобедренном треугольнике углы, при основании равны. 2) Обратно, если в треугольнике два угла равны, то он равнобедренный.

Доказательство. 1) Пусть – равнобедренный, т.е. . Докажем, что (рис. 2.23). Рассмотрим биссектрису , проведенную из вершины к основанию . Тогда из равенства , показанного в доказательстве теоремы 3, вытекает равенство . 2) Пусть в треугольнике (рис. 2.23). Покажем, что – равнобедренный.

По второму признаку равенства треугольников , так как . Здесь в записях и изменен порядок вершин. Поэтому сторона в соответствует стороне в , и сторона в соответствует стороне в . В общем случае и разные. Поэтому основание треугольника соответствует основанию треугольника .

Итак, из равенства вытекает равенство . Теорема доказана. Теорема 4 состоит из двух теорем (утверждений): теоремы 1) и теоремы 2). Теорема 2) называется обратной теореме 1). Смысл сказанного следует понимать так: условие теоремы 1) («треугольник равнобедренный») является заключением теоремы 2). условие теоремы 2) («в треугольнике два угла равны», или «в треугольнике углы при основании равны») является заключением теоремы 2). Другими словами, через обозначим утверждение о том, что «треугольник равнобедренный», а через обозначим утверждение о том, что «в треугольнике два угла равны», или «в треугольнике углы при основании равны». Тогда теорему 1) можно записать в виде: , а теорему 2) – в виде: . Во многих случаях, объединяя подобные два предложения, записывают так: . Эта запись читается следующим образом: Для того чтобы, треугольник был равнобедренным, необходимо и достаточно, чтобы углы при его основании были равные.

Не всякая теорема имеет обратную теорему, т.е. если данная теорема верна, то обратное ей утверждение не всегда может быть верным.

Например, рассмотрим теорему: «Сумма смежных углов равна 180%. Обратное этому утверждение записывается так: «Если сумма двух углов равна 180°, то эти углы смежные». Очевидно, что последнее утверждение не верно, ибо не все углы, сумма которых равна 180°, являются смежными. Для того чтобы такие углы были смежными, необходимо также, чтобы они имели общую сторону и общую вершину.

Пример с решением №2

Докажем, что у равностороннего треугольника все углы равны. Решение:

Пусть — данный равносторонний треугольник: . Так как , то – равнобедренный с основанием . Тогда по теореме 3 . Также, поскольку , то А – равнобедренный с основанием и поэтому . Следовательно, (рис. 2.22).

Третий признак равенства треугольников

Теорема 5. (Признак равенства треугольников по трем сторонам.) Если три стороны, одного треугольника равны. соответственно трем сторонам другого треугольника, то такие треугольники равны. Доказательство. Пусть даны треугольники и такие, что . Докажем, что . Равенство треугольников и можно доказать, предполагая, что . Тогда . Иначе эти треугольники были бы равны по I признаку. Предположим, что треугольник равен треугольнику , у которого вершина лежит в одной полуплоскости с вершиной относительно прямой (рис. 2.24). Пусть – середина отрезка . Треугольники и равнобедренные с общим основанием . Поэтому их медианы и являются высотами. Значит, прямые и перпендикулярны прямой . Прямые и не совпадают, так как точки не лежат на одной прямой. Но через точку к прямой можно провести только одну перпендикулярную прямую. Мы пришли к противоречию. Следовательно, .

Пример с решением №3

Пусть даны треугольники и такие, что . Докажем, что . Решение:

Построим треугольник , равный треугольнику , и треугольник равный треугольнику (рис. 2.25). Так как , то точки и , лежат соответственно на прямых и . Поэтому (по III признаку равенства треугольников), т.к. . Следовательно, . Тогда по I признаку равенства треугольников , т.к. .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.

Признаки равенства треугольников

Два треугольника считаются равными, если их можно совместить наложением. Но, чтобы не выполнять каждый раз наложение, для доказательства равенства треугольников, установили три признака, по которым можно определить, совместятся треугольники или нет. Эти признаки называются признаками равенства треугольников.

Первый признак равенства треугольников

Теорема:

Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.

Доказательство:

Рассмотрим два треугольника ABC и A₁B₁C₁, у которых:

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить A₁B₁C₁ на ABC так, чтобы точка A₁ совместилась с точкой A и сторона A₁B₁ совместилась со стороной AB, то точка B совместится с точкой B₁, так как A₁B₁ = AB. Сторона A₁C₁ совместится со стороной AC, так как ∠A = ∠A₁. Точка C₁ совпадёт с точкой C, так как A₁C₁ = AC. Стороны B₁C₁ и BC совместятся, так как совместились их концы. Таким образом, треугольники совместятся. Теорема доказана.

Второй признак равенства треугольников

Теорема:

Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла.

Доказательство:

Рассмотрим два треугольника ABC и A₁B₁C₁, у которых:

AC = A₁C₁, ∠A = ∠A₁ и ∠C = ∠C₁.

Требуется доказать, что

ABC = A₁B₁C₁.

Если наложить A₁B₁C₁ на ABC так, чтобы точка A₁ совместилась с точкой A и сторона A₁C₁ совместилась со стороной AC, то точка C₁ совпадёт с точкой C, так как A₁C₁ = AC. Сторона A₁B₁ совпадёт со стороной AB, так как ∠A = ∠A₁. Сторона C₁B₁ совпадёт со стороной CB, так как ∠C = ∠C₁. Вершина B₁ совпадёт с вершиной B, так как B и B₁ будут служить точками пересечения одних и тех же отрезков. Таким образом, треугольники совместятся. Теорема доказана.

Третий признак равенства треугольников

Теорема:

Два треугольника равны, если три стороны одного треугольника равны трём сторонам другого.

Доказательство:

Рассмотрим два треугольника ABC и A₁B₁C₁, у которых:

Требуется доказать, что

ABC = A₁B₁C₁.

Приложим треугольники ABC и A₁B₁C₁ один к другому так, чтобы вершина A совместилась с A₁, вершина C — с C₁, а вершины B и B₁ оказались по разные стороны от прямой AC.

Соединив точки B и B₁, получим два равнобедренных треугольника BAB₁ и BСB₁.

В треугольнике BAB₁ ∠1 = ∠4, в BСB₁ ∠2 = ∠3 (как углы при основании). Следовательно,

∠1 + ∠2 = ∠4 + ∠3, поэтому ∠ABC = ∠AB₁C.

Итак, AB = A₁B₁, BC = B₁C₁, ∠ABC = ∠A₁B₁C₁.

Из этого следует, что треугольники ABC и A₁B₁C₁ равны по первому признаку равенства треугольников. Теорема доказана.

Признаки равенства прямоугольных треугольников

Для прямоугольных треугольников, кроме перечисленных трёх признаков равенства, имеются ещё дополнительные признаки, так как у них у всех есть прямой угол, а все прямые углы равны между собой.

Подобие треугольников (ЕГЭ — 2022)

Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.

А вот что такое подобные треугольники? Вроде как «похожие», но как это понимать? И для чего это понимать?

Ну например для решения задание ЕГЭ №16, где подобие треугольников используется для доказательств. Кстати, полностью 16-ю задачу решают менее 1% выпускников!

Читай эту статью, смотри вебинар по 16 задаче и все поймешь!

Подобие треугольников — коротко о главном

Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия ( displaystyle k).

( angle A = angle ,angle B = angle ,angle C = angle )

Отношение периметров подобных треугольников равно коэффициенту подобия: ( displaystyle frac_>>_>_>_>>>>=k).

Отношение площадей подобных треугольников равно квадрату коэффициента подобия: ( displaystyle frac_>>_>_>_>>>>=^>).

Признаки подобия треугольников:

По двум углам:

По одному углу и отношению заключающих его сторон:

По отношению трех сторон:

Подобные треугольники — подробнее

Мы разобрали подробно все, что касается треугольников в общем. Кроме того мы рассмотрели отдельные темы:

Но что такое подобные треугольники?

Вот, например, такой и такой:

Похожи эти треугольники? Ты скажешь, конечно же нет!

А такой и такой?

А вот такой и такой?

Посмотри внимательно, тоже похожи.

А теперь строго математически!

Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.

То есть все углы равны и все стороны одного треугольника в ( displaystyle 5), или, в ( displaystyle 7), или в ( displaystyle 8,21) (или и т.д.) больше сторон другого треугольника.

Записываются слова «треугольник ( displaystyle ABC) подобен треугольнику ( displaystyle >_>_>)» с помощью такого значка:

То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы ( displaystyle k).

(angle A = angle ,angle B = angle ,angle C = angle )

Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон.

И они придумали признаки подобия треугольников .

Признак подобия треугольников «по двум углам»

Если два угла одного треугольника равны двум углам другого треугольника , то такие треугольники подобны.

Помнишь еще, что «( displaystyle sim)» обозначает слова «подобен»?

Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак.

Но есть и еще два. Смотри.

Признак подобия треугольников «две пропорциональные стороны и угол между ними»

Если треугольники имеют одинаковый угол, и стороны, заключающие этот угол, пропорциональны , то такие треугольники подобны.

( displaystyle left| beginangle A=angle >\frac<>_>>=frac<>_>>end right.Rightarrow Delta ABCsim>_>_>)

Признак подобия треугольников «три пропорциональные стороны»

Если три стороны одного треугольника пропорциональны сторонам другого треугольника , то такие треугольники подобны.

( displaystyle frac>_>>=frac>_>>=frac<_>_>>Rightarrow Delta ABCsim<_>_>_>)

Самый главный «секрет» подобия треугольников

Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным?

Ну вот, что же хорошего? А то, что тогда…

Все элементы одного треугольника ровно в ( displaystyle 2) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника.

Не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д.

Есть одно важное исключение: площадь .

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 16. Подобие треугольников. Задачи на доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.

Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).

Признаки равенства треугольников

Чего только не приходится делать на уроках геометрии! Но нет ничего приятнее, чем сесть и доказать равенство треугольников, используя три признака равенства.

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Познавайте математику вместе с нашими лучшими преподавателями на курсах по математике для учеников с 1 до 11 класса!

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

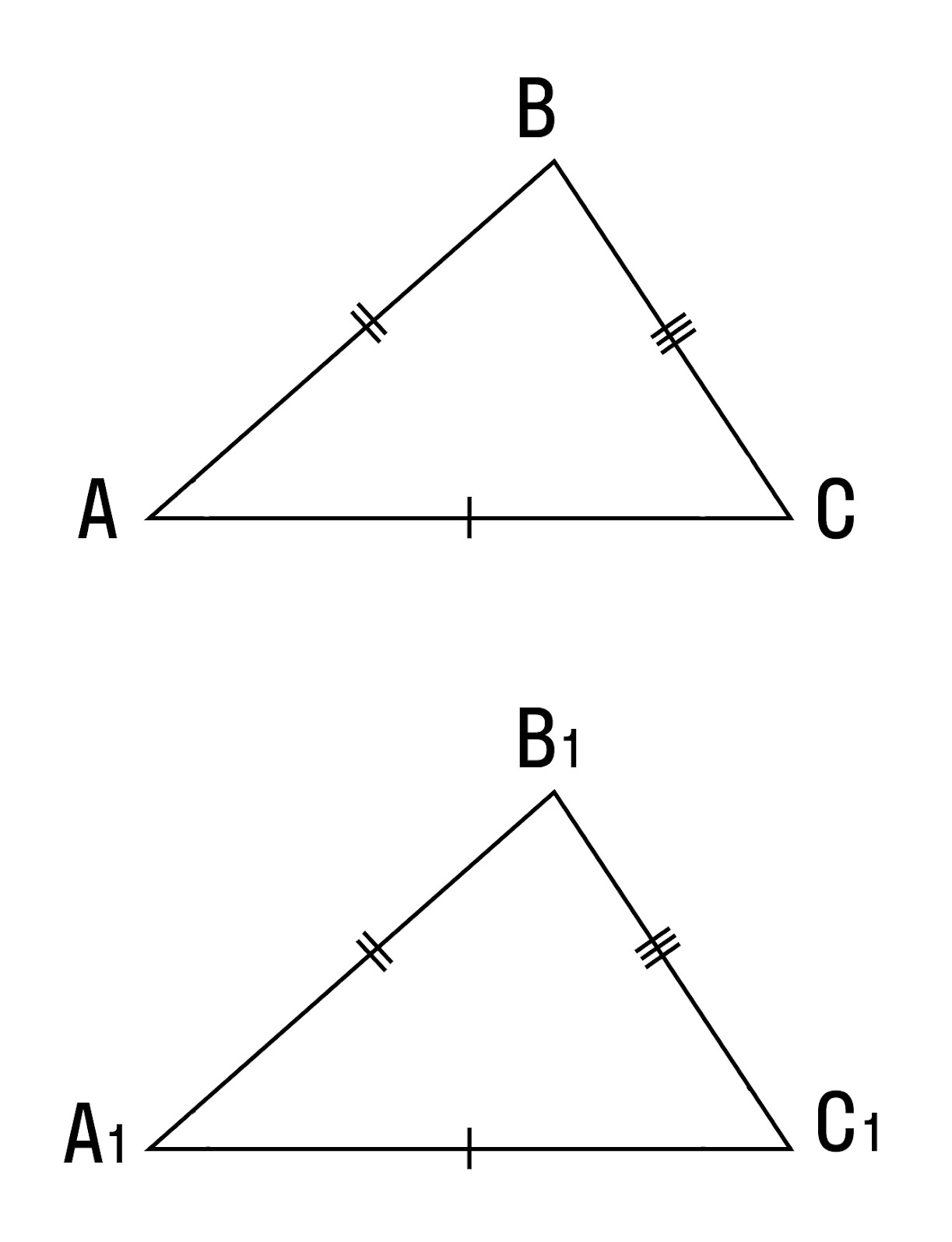
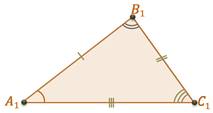
Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.