Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам

Определение длины окружности через диаметр или радиус

При решении задач и в повседневной жизни можно встретить множество предметов круглой формы, в связи с чем возникает необходимость в их измерении. К примеру, для расчета объема материала, необходимого для производства круглого стакана определенного размера, потребуется построить и найти длину его окружности.

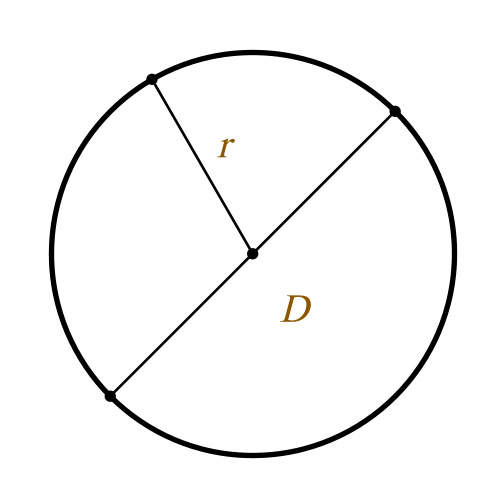
Окружность представляет собой замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки.

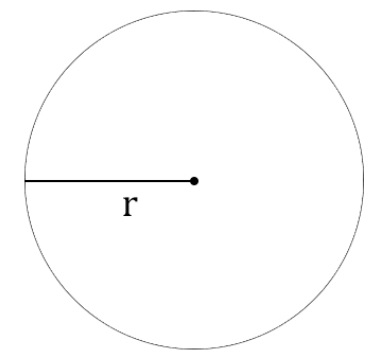
Рассматриваемая в рамках этого определения точка является центром окружности. Если соединить центр с любой точкой, принадлежащей окружности, то получится радиус. Радиусом также называют длину данного отрезка.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Радиус окружности является прямым отрезком, который выходит из центра окружности и проведен до ее границы.

Таким образом, радиус окружности соединяет ее центр с точкой, расположенной на этой окружности. Для обозначения радиуса используют r.

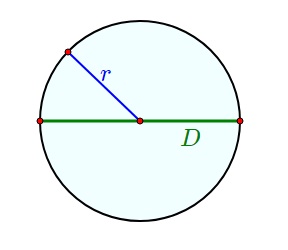
Диаметр окружности – является прямым отрезком, который соединяет две точки, расположенные на границе окружности, и проходит через центр этой окружности.

Данный параметр обозначают D или d.

Как рассчитать через диаметр или радиус

Длина окружности также является периметром этой окружности. Для расчета длины или периметра круга необходимо знать диаметр или радиус.

Формулы для вычисления длины окружности:

(L = 2 pi rL=2pi r)

где L – является длиной окружности;

D – определяется, как диаметр окружности;

r – представляет собой радиус окружности;

(pi) – это число Пи, равное примерно 3,14.

Исходя из представленных формул для расчета длины окружности, можно вывести соотношение радиуса и диаметра окружности:

Основные формулы с пояснением

Обладая информацией о радиусе и диаметре окружности, достаточно просто рассчитать ее длину. Однако не во всех задачах присутствуют эти данные. Есть ряд примеров, в которых определить длину окружности необходимо с помощью параметров другой геометрической фигуры.

Вычисление длины окружности через площадь круга

В том случае, когда известна площадь круга, можно рассчитать длину окружности по формуле:

где (pi) — является числом пи, значение которого равно 3,14;

S — определяет площадь круга

Расчет длины окружности через диагональ вписанного прямоугольника

В задачах можно встретить примеры вписанного в окружность прямоугольника.

В этом случае длина окружности рассчитывается по формуле:

где ( pi) — является числом пи, значение которого равно 3,14;

d — является диагональю рассматриваемого прямоугольника.

Как вычислить длину окружности через сторону описанного квадрата

В том случае, когда окружность вписана в квадрат с прямыми углами, сторона которого известна, можно определить длину этой окружности.

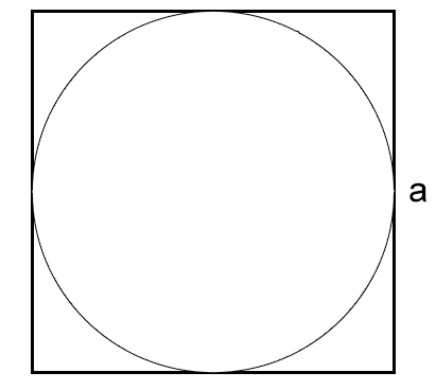
где (pi ) — является числом пи, значение которого равно 3,14;

a — определяет длину стороны квадрата

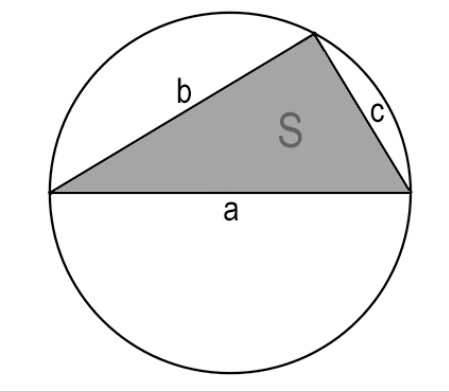
Расчет длины окружности с помощью сторон и площади вписанного треугольника

Предположим, что в окружность вписан треугольник. Если имеется информация о всех его трех сторонах, а также площади, то можно рассчитать длину окружности, оперируя следующей формулой:

где (pi) — математическая константа со значением 3,14;

a — является первой стороной треугольника;

b — является второй стороной треугольника;

с – является третьей стороной треугольника;

S – определяется, как площадь рассматриваемого треугольника.

Способ нахождения длины окружности при известной площади и полупериметру описанного треугольника

Представим, что в какой-то треугольник вписана окружность. Известно значение площади треугольники и его полупериметр. Необходимо рассчитать длину окружности. Следует заметить, что периметром треугольника называют сумму всех его сторон, а полупериметр составляет половину этой суммы. Таким образом, для нахождения полупериметра нужно определить периметр треугольника и разделить его на два.

Формула расчета длины окружности:

где (pi) — математическая константа со значением 3,14;

S — является площадью треугольника;

p — представляет собой полупериметр треугольника.

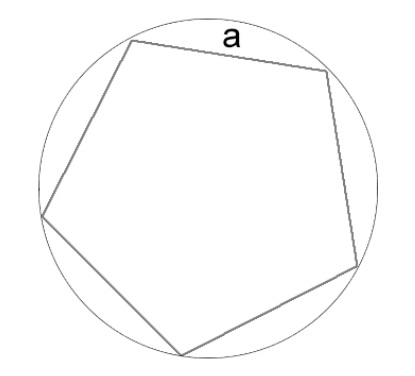
Как вычислить длину окружности через сторону вписанного правильного многоугольника

Когда в окружность вписан правильный многоугольник, в первую очередь стоит сосчитать количество его сторон. Также требуется знать длину стороны этой геометрической фигуры. Стороны правильного многоугольника одинаковы, как у квадрата. В этом случае формула для расчета длины окружности имеет вид:

где (pi) — математическая константа со значением 3,14;

a — это сторона многоугольника;

N — определяет количество сторон многоугольника.

Примеры решения задач

Необходимо рассчитать, какова длина окружности, если ее диаметр составляет 5 см.

При известном диаметре окружности можно рассчитать ее длину с помощью формулы:

Подставив известные из условия задачи значения, получим:

(L = pi D = 3,14 * 5 = 15,7) (см)

Ответ: длина окружности равна 15,7 см.

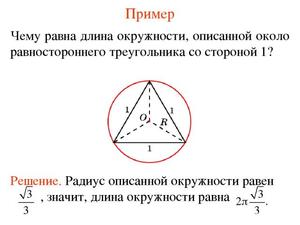
Требуется определить длину окружности, описанной вокруг правильного треугольника, сторона которого составляет (a=4sqrt) дм.

Радиус окружности составляет:

При подстановке переменных формула будет изменена:

При известном радиусе окружности можно рассчитать длину рассматриваемой окружности, используя соответствующую формулу:

(L = 2 pi r=2 pi *4=2*3,14*4=25,12) (дм)

Ответ: длина окружности составляет 25,12 дм.

Дана окружность, радиус которой равен 2 см. Требуется рассчитать длину окружности.

L = 3.14 * 4 = 12,56 (см)

Ответ: длина окружности равна 12,56 см.

Имеется окружность с радиусом 3 см. Необходимо определить длину данной окружности.

Длина окружности: формулы поиска по радиусу, равному половине диаметра

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.

Это интересно: что такое горизонтально, что означает слово горизонталь?

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Вычислить длину окружности по диаметру, онлайн калькулятор

Нормальное ускорение при движении по окружности, онлайн расчет

Расчет нормального ускорения, радиуса окружности и линейной скорость, при движении по окружности. Нормальное ускорение при движении по окружности, онлайн расчет

Через диагональ

Формула для нахождения длины окружности через диагональ:

, где d — диагональ окружности.

Как рассчитать диаметр по длине,площади или радиусу окружности формула

Найти какой диаметр окружности можно в нашем онлайн калькуляторе даже не зная формул, просто введите цифры и получите результат

Условные обозначения в формулах

Р- длина окружности
п- число п = 3,14159
R- радиус окружности
D- диаметр окружности
S- площадь круга

Формула расчёта по диаметру

Как вычислить длину окружности через площадь круга

Умножьте число пи на четыре площади круга.

Найдите корень из результата.

O — искомая длина окружности.
S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

Как найти длину окружности через диагональ вписанного прямоугольника

Умножьте число пи на диагональ.

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d – любая диагональ прямоугольника.

Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга

Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его. Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.

Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.

Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра. Данное вычисление вытекает из формулы площади круга, A = πr 2 , преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см 2 , разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.

Вычисление диаметра окружности из чертежа окружности

Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой. Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.

Начертите две пересекающиеся окружности, одну – с центром в точке A, а другую – с центром в точке B. Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.

Через две точки, в которых окружности пересеклись, проведите прямую. Отрезок этой прямой между двумя точками и будет равен диаметру окружности.

Измерьте диаметр. Измерьте его с помощью линейки, а если нужна большая точность – штангенциркулем с цифровой индикацией. Готово!

Как вычислить длину окружности через сторону описанного квадрата

Умножьте число пи на сторону квадрата.

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
a – любая сторона квадрата.

Периметры фигур

Расчет периметра квадрата, прямоугольника, треугольника, круга (периметры фигур). Периметры фигур

Формула вычисления длины/периметра

1. Через радиус

Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π :

C = 2 * π * r

Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.

2. Через диаметр

Периметр/длина окружности считается как произведение ее диаметра на число π :

C = π * d

Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.

Примечание: в расчетах значение числа π округляется до 3,14.

Вычисление площади круга и длины окружности, когда радиус или диаметр выражены переменными

Найдите радиус или диаметр окружности. В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.

Пример: вычислите длину окружности с радиусом (х + 1).

Напишите формулу с данным значением. Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.

Пример: вычислите длину окружности с радиусом (х + 1).
Напишите формулу: C = 2πr
Подставьте данное значение: C = 2π(х + 1)

Вычислите длину окружности так, как если бы переменная была представлена числом. На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.

Пример: вычислите длину окружности с радиусом (х + 1).
C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.

Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.

Найдите площадь круга с радиусом 2х.
- A = πr 2 = π(2x) 2 = π4x 2 = 12,56x 2
- A = π(d/2) 2 = π((x +2)/2) 2 = ((x +2) 2 /4)π
Уравнение окружности

2. Уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

x = a + r cos t

y = b + r sin t

Касательная окружности и ее свойства

Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Площадь круга и его частей. Длина окружности и ее дуг

Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь круга

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Длина окружности

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

Площадь круга

Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .

Таким образом, площадь круга радиуса R , обозначаемая S , равна

Длина окружности

то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :

Следствие . Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

Урок 25 Бесплатно Длина окружности и площадь круга

На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.

Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.

Узнаем, как рассчитать длину окружности и площадь круга.

Окружность и круг

Мы часто встречаем такие понятия, как окружность и круг.

Давайте попробуем разобраться, что называют окружностью, а что кругом.

Окружность – это замкнутая плоская кривая, все точки которой удалены на одинаковые расстояния от заданной точки, называемой центром окружности.

Центр окружности– это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.

По сути, окружность – это изогнутая линия. Наглядно представить данную геометрическую фигуру можно, обведя стакан или блюдце карандашом, – оставшийся нарисованный след и будет окружностью.

Круг – это часть плоскости, ограниченная окружностью. Можно также сказать что это часть плоскости, которая находится внутри линии окружности.

Круг – плоская фигура, ее можно получить, закрасив окружность или вырезав его из бумаги по контуру окружности.

Свои имена окружность и круг приобрели не сразу.

В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.

Только в Древней Греции окружность и круг приобрели себе свои названия.

Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.

У меня есть дополнительная информация к этой части урока!

Древние греки считали круг и окружность символом бесконечности и совершенства. Поражало то, что в каждой своей точке окружность устроена одинаково, представляя собой бесконечную линию, которая движется сама по себе.

У древних славян еще за долго до христианства круг был символом солнца.

В Древнем Египте и Греции круг изображали в виде змея Уробороса, который кусает свой хвост, образуя тем самым, окружность – этот символ обозначал бесконечность и цикличность во всей вселенной (смена дня и ночи, жизни и смерти т.д.).

Символика круга в различных религиях сопоставляется с целостностью, вечностью и бесконечной мудростью.

Например, в масонских учениях круг как форма без начала и конца – это источник бесконечного времени и пространства, в котором заключена тайна творения.

У буддистов круг символизирует единство внутреннего и внешнего мира.

В дзен-буддизме круг – это символ высшей степени просветления и совершенства. На основе этого представления построены принципы инь и янь (в виде круга, разделенного на две части, – символа взаимодействия и борьбы двух начал).

В христианстве круг служит эталоном божественного и духовного совершенства.

В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.

Рассмотрим подробней элементы, характерные для окружности.

Радиус окружности– это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.

С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.

Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.

Радиус обозначается маленькой латинской буквой (r) или заглавной (R).

В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.

Диаметр – это отрезок прямой, проходящий через центр окружности и соединяющий две точки на этой окружности.

Диаметр в переводе с греческого (diametros) – поперечник.

Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.

По величине диаметр равен двум радиусам, лежащим на одной прямой.

d = 2r

Следовательно, радиус- это половина диаметра.

r = d: 2

Пример 1

Радиус окружности равен 6 см.

Чему равен диаметр окружности?

r = 6 см

d – ?

Решение:

d = 2r

d = 2r= 2*6 = 12 (см) диаметр окружности

Ответ: d= 12 см

Пример 2

Диаметр окружности равен 12 см.

Чему равен радиус окружности?

d = 12 см

r – ?

Решение:

r = d : 2

r = 12 : 2 = 6 (см) радиус окружности

Ответ: r = 6 см

У меня есть дополнительная информация к этой части урока!

Секущая окружности – это прямая, пересекающая окружность в двух точках. В результате окружность делится на дуги.

Точки А и В – точки пересечения секущей с окружностью.

Образовались две дуги: (mathbf)

Отрезок, который соединяет любые две точки на окружности (отрезок секущей), называется хордой.

Отрезок АВ (отрезок секущей) на рисунке – хорда окружности.

Хорда в переводе с греческого – струна, тетива.

На рисунке отрезок MN является хордой.

Если хорда проходит через центр окружности, то она является самой большой хордой для этой окружности. По своей сути она является диаметром для данной окружности и делит окружность на две равные дуги.

По мере удаления хорды от центра размеры ее уменьшаются, а дуги делятся на большую и малую.

АВ– самая большая хорда окружности- диаметр окружности.

CD, N₁M₁_, NM, FE– хорды окружности.

Хорды окружности, удаленные на равные расстояния от центра, равны.

Хорды NM и N₁M₁ равны.

Если две хорды пересекаются в точке, то их отрезки пропорциональны.

Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.

Пройти тест и получить оценку можно после входа или регистрации

Длина окружности и площадь круга

Давайте выясним, что такое длина окружности и как ее определить.

Представьте, что окружность обернута нитью.

Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.

Обычно длина окружности обозначается заглавной буквой С

Длина окружности (С) зависит от длины ее диаметра (d)

Обратите внимание на рисунок.

Вы можете заметить, что чем больше диаметр, тем больше длина окружности.

Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.

А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.

Это число (коэффициент пропорциональности) обозначают греческой буквой (mathbf), читается «пи».

С– это длина окружности

d– диаметр окружности

запишем отношение (mathbf)

отсюда следует, что длина окружности равна

Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности

Выясним, чему равна постоянная величина – число (mathbf)

Число (mathbf)- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.

У меня есть дополнительная информация к этой части урока!

История числа (mathbf< pi>) насчитывает около 4 тысячелетий.

Одно из первых доказательств древнего существования этого числа (mathbf< pi>) заключено в папирусе Ахмеса, в одном из старейших задачников (1650 год до н.э.), найденного в Древнем Египте.

В папирусе дано достаточно точное, особенного для того времени, значение числа, равного 3,1605.

Точнее число (mathbf< pi>) рассчитал древнегреческий математик Архимед. Он приближенно представил значение константы в виде обыкновенной дроби (mathbf>)

Архимеду удалось найти точное приближение числа (mathbf< pi>) (т.е. узкий числовой промежуток к которому принадлежит число (mathbf< pi>)).

Это приближение выглядело так (mathbf)

С течением времени находили все более точные значения постоянной.

И спустя восемь веков математиком Людольфом ван Цейленом были определены точно 36 знаков после запятой.

Кстати, число существовало, велись его подсчеты и уточнения, а конкретного имени эта постоянная не имела.

Буквенное значение, такое, какое оно сейчас есть ((mathbf< pi>)), константа получила в начале XVIII века.

Название предложил ученый Джонс, и, спустя тридцать лет, имя этой постоянной стало общепризнанным.

К числу (mathbf< pi>) до сих пор не потерян интерес.

Точность значения постоянной уже составляет десять триллионов символов после запятой.

Открываются клубы интересов, математические сообщества по изучению числа (mathbf< pi>)

Придуманы различные методики запоминания числа (mathbf< pi>) с точностью до десятков тысяч знаков после запятой.

Мы с вами не будем оперировать настолько точными данными.

Для вычислений и решения задач нам будет хватать округления числа (mathbf< pi>) до сотых.

И будем принимать число (mathbf< pi>) приблизительно равным 3,14.

Число (mathbf< pi>) используют во многих математических и физических формулах.

Площадь круга

Так как круг – это часть плоскости, то одной из его характеристик является площадь.

Площадь круга равна произведению квадрата радиуса на число (mathbf< pi>).

Где S– это площадь круга

r– радиус круга

(mathbf< pi>) – постоянная величина

Так как (mathbf = frac d>), то получаем еще одну формулу для определения площади круга

Пройти тест и получить оценку можно после входа или регистрации

Решения задач по теме «Длина окружности и площадь круга»

Рассмотрим примеры решения задач

Задача 1

Найдите длину окружности, если ее радиус равен 4 см.

Число (mathbf<>) округлите до сотых.

r = 4 см

Длину окружности С – ?

Решение:

Подставив в формулу известные значения радиуса и постоянной (mathbf), получим:

Ответ: (mathbf)(см)

Задача 2

Длина окружности надувного бассейна 15,7м.

Найдите диаметр этого бассейна.

Число (mathbf) округлите до сотых.

C = 15,7 м

Диаметр d – ?

Решение:

Подставив в формулу известные значения длины окружности и постоянной (mathbf), получим:

Ответ: (mathbf) (м)

Задача 3

Диаметр окружности равен 6 см.

Найдите площадь круга, ограниченного этой окружностью.

Значение числа (mathbf) округлить до сотых.

d = 6 cм

Площадь круга S – ?

Решение:

Подставим в формулу известные значения диаметра окружности и постоянной , получим:

(mathbf3,146^2 = frac <3,1436> > = 3,149=28,26) (cм 2 ) площадь круга

Ответ: (mathbf) (см 2 )

Задача 4

Вычислите площадь полукруга, если радиус круга равен 5 см.

Значение (mathbf) округлить до целых.

r = 5 cм

Площадь полукруга S_п – ?

Решение:

Площадь круга найдем по формуле:

Площадь полукруга будет равна половине площади всего круга.

Следовательно, формула для расчета площади полукруга получится вида:

Подставим в формулу известные значения радиуса круга и постоянной (mathbf), получим:

(mathbf =37,5>) (cм 2 ) площадь полукруга

Ответ: (mathbf) (см 2 )

Задача 5

Найдите площадь круга, если известна длина окружности С.

Длина окружности С

Площадь круга S – ?

Решение:

Длина окружности выражается формулой:

Выразим неизвестный радиус окружности через длину окружности:

Площадь круга определяем по формуле:

Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:

Сократим полученную дробь:

У меня есть дополнительная информация к этой части урока!

Кроме вычислительных задач, существуют задачи на построение окружности и круга.

Окружность и круг можно начертить с помощью чертежного инструмента, который называется циркуль.

В переводе с латинского языка circulus означает «окружность», «круг».

Циркуль использовали еще с древности, много тысяч лет назад, об этом свидетельствуют найденные на раскопках находки, изображения.

Циркуль представляет собой две одинаковые по длине «ножки». На конце одной из них игла, а на второй- грифель.

Есть циркуль, у которого вместо «ножки» с грифелем помещается карандаш.

Рассмотрим, как построить окружность (круг) на бумаге с помощью циркуля и линейки.

Если задан радиус окружности (круга), то в нулевую отметку на линейке ставим иголку циркуля, другая «ножка» циркуля с грифелем в точку на линейке, равной по значению заданному радиусу.

Ставим точку на листе бумаги – это будет центр окружности (круга), в эту точку ставим иголку циркуля.

Не отрывая грифеля второй «ножки» циркуля от бумаги проводим окружность с заданным радиусом.

Если в задаче задан диаметр, то, прежде чем совершать замер по линейке, необходимо диаметр разделить пополам.

Таким образом, устанавливаем раствор циркуля по линейке на расстояние d:2 = r и чертим окружность по выше изложенной схеме.

Чтобы начертить окружность на местности, пользуются колышком и веревкой. Колышек вбивают в землю – предполагаемый центр окружности; веревка одним концом закрепляется к этому колышку, второй конец веревки туго натягивается; далее очерчивают окружность.

Данный способ построения окружности (круга) может быть применен и на бумаге, если под рукой не оказалось циркуля.

В качестве колышка берется кнопка, к ней привязывается нить определенной длинны (длина нити равна значению заданного радиуса), ко второму концу привязывается карандаш

Длина окружности

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.

Определение длины окружности

Формула расчёта длинны окружности

Произвести расчёт окружности можно по следующей формуле:

r – радиус окружности

D – диаметр окружности

L – длина окружности

Пример нахождения длинны окружности

Вычислить длину окружности, имеющей радиус 10 сантиметров.

Формула для вычисления дины окружности имеет вид:

где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 31,4 сантиметра

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Похожие записи: