Как вычислить площадь: формулы расчета для разных фигур, знаки обозначения, единицы измерения

Формула площади

Геометрия, как часть математики, рассматривает целый ряд геометрических фигур: круг, квадрат, прямоугольник, треугольник и многих других.

Геометрические фигуры являются множеством точек на плоской поверхности, которые соединяются прямыми и на выходе становятся разными фигурами с разными особенностями.

Параметры геометрических фигур, такие как длины сторон, периметр, площадь, можно находить разными способами в зависимости от типа фигуры.

Площадь — параметр измерения геометрической фигуры, который передает информацию о ее размере.

Площадь в геометрии обозначается знаком S, от английского square — площадь. Понятием площади пользуются как люди науки — математики, физики, так и люди рабочих профессий, например, строители.

Данная характеристика измеряется в единицах измерения в квадрате, например, квадратный сантиметр ( с м 2 ), квадратный метр ( м 2 ), гектар (га).

Квадрат и прямоугольник являются фигурами, у которых есть по 4 прямых угла. Их отличает только длина сторон — у прямоугольника не все 4 стороны равны, они равны попарно относительно противоположных.

Площадь правильно построенного прямоугольника можно найти через перемножение его сторон друг на друга.

Формула нахождения площади прямоугольника будет записана следующим образом:

где a и b являются сторонами прямоугольника.

С помощью данной формулы можно найти площади классов или комнат, а также стен, что может помочь как в решении математических, так и бытовых задач.

3d моделью прямоугольника можно считать параллелепипед.

Площадь квадрата можно найти двумя способами:

• по длине стороны в квадрате;
• по длине диагонали.

Расчет площади квадрата по длине стороны в квадрате:

Куб представляет собой 3 d модель квадрата. Чтобы найти площадь оболочки куба, а не его полного объема, нужно сложить шесть его площадей квадрата.

Так как квадрат является частным случаем прямоугольника, его площадь также можно найти по формуле S = a × b , однако в таком случае a и b будут равны, а формула по смыслу будет повторять выше написанную.

В некоторых случаях необходимо нахождение площади квадрата через диагональ. Это может быть связано с решением определенной геометрической задачи или в связи с практическим удобством.

Формула площади квадрата через его диагонали:

где a — длина сторон квадрата;

d — длина диагоналей квадрата.

Формула площади для круга и эллипса

Круг и эллипс относятся к фигурам, которые состоят из множества точек, соединенных кривыми. Данные фигуры не содержат углов, однако это не значит, что у них нельзя найти площадь.

Площадь круга можно найти двумя способами:

• через радиус;
• через диаметр.

Радиус является отрезком, соединяющим центр окружности и точку на самой окружности.

Вычисление площади круга по радиусу будет производиться по формуле:

где π — постоянная Пи, равна 3,14.

Диаметр, в отличие от радиуса, соединяет 2 точки на окружности, но при этом также проходит через ее центр. По сути, диаметр является удвоенным радиусом.

Формула площади круга через диаметр:

где π — постоянная Пи, равна 3,14.

Через знание формулы площади круга и прямоугольника можно узнать площадь оболочки цилиндра: боковые стороны будут кругами, а основная часть — свернутым прямоугольником.

Эллипс отличается от круга тем, что его радиусы и диагонали не равны, так как некоторые его части находятся на большем отдалении от цента, чем другие.

Для нахождения площади эллипса необходимо знать его оси.

Осями эллипса являются диагонали эллипса, проведенные через самые ближние точки самого эллипса и центр и через самые дальние точки самого эллипса и центр.

Подсчет площади эллипса происходит через произведение длин большой и малой полуосей эллипса и числа пи:

Формула площади для параллелограмма, ромба и трапеции

Параллелограмм, ромб и трапеция отличаются от квадрата и прямоугольника тем, что не все их углы имеют 90°. Из-за этого их площадь изменится, даже при равных значениях сторон, по отношению к площади квадрата и прямоугольника.

Параллелограмм является четырехугольником, чьи стороны попарно параллельны. Частными случаями данной фигуры являются прямоугольник, квадрат и ромб.

Площадь параллелограмма можно найти тремя способами:

• через сторону и высоту;
• через две стороны и величину угла между ними;
• через диагонали и угол между ними.

Формула площади параллелограмма через сторону и высоту приобретет следующий вид:

где a — сторона, к которой проведена высота,

h — высота непосредственно.

Посчитать площадь параллелограмма через две стороны и угол между ними можно так:

Нахождение площади параллелограмма через диагонали и угол между ними:

S = 1 2 × d 1 × d 2 × sin y

где d 1 и d 2 — это диагонали параллелограмма,

y — угол между ними.

Ромб является частным случаем параллелограмма, чьи стороны равны.

Его площадь можно найти тремя способами:

• по длине стороны и высоте;
• по длине стороны и углу;
• по длинам его диагоналей.

Формула площади ромба по стороне и высоте выглядит так же, как и площадь параллелограмма по таким же характеристикам, с условием, что все высоты ромба будут равны:

Формула площади ромба через длину сторон и углу между ними похожа на соответствующую формулу площади параллелограмма с условием того, что стороны равны, а значит их перемножение можно заменить квадратом величины стороны:

Считать площадь ромба через диагонали можно так:

S = 1 2 × d 1 × d 2

Трапеция имеет четыре угла, которые не равны между собой, но в сумме дают 360°. Две стороны данной фигуры параллельны, а две другие — нет. Параллельные стороны считаются основаниями трапеции, непараллельные — боковыми сторонами.

Площадь трапеции можно найти двумя способами:

• по формуле Герона;
• по длине основ и высоте.

Формула Герона для трапеции:

S = a + b a – b p – a p – b p – a – c p – a – d

где a, b — длины оснований трапеции,

c, d — длины боковых сторон,

p = a + b + c + d 2

Узнать площадь ромба по длине основ и высоте можно по формуле:

Формула площади треугольника по гипотенузе и острому углу

Треугольник является геометрической фигурой, имеющей три угла и три прямых, соединяющих их. Все треугольники делятся:

• по величине углов на острые, тупые и прямоугольные;
• по числу равных сторон на разносторонние, равносторонние и равнобедренные.

Одной из возможных формул нахождения площади треугольника является формула:

S = 0 , 25 × c 2 × sin 2 a

где c — гипотенуза,

a — любой из прилежащих острых углов.

Определение площади треугольника другими способами

Помимо этого, площадь треугольника также можно найти через:

• сторону и высоту;
• через три стороны;
• через две стороны и угол между ними;
• через три стороны и радиус описанной окружности;
• через три стороны и радиус вписанной окружности.

Через сторону и высоту:

Через три стороны:

S = p ( p – a ) p – b p – c

где р — полупериметр.

p = a + b + c + d 2

Через две стороны и угол между ними:

S = 1 2 × a × b × sin y

Через три стороны и радиус описанной окружности:

где р — полупериметр.

p = a + b + c + d 2

Следует отметить, что находить площадь геометрических фигур можно через другие фигуры, когда, например, их разбивают на части. Так, площадь квадрата можно найти, сложив площади двух треугольников, а площадь параллелограмма — через сумму площади двух треугольников и прямоугольника или квадрата.

Примеры решения задач

Сколько квадратных баночек с площадью основания 0 , 1 м 2 поместится в коробке со стороной 30 см?

Решение: S = 30 2 = 900 с м 2 или 0 , 9 м 2 , следовательно, 0,9:0,1 = 9 баночек.

Известно, что по диагонали квадратной танцевальной площадки по заданию проектировщика должна висеть деревянная перегородка. Длина заранее купленной перегородки составляет 6 м. Какова площадь самой площадки?

Решение: S = 1 2 × 6 2 = 18 м 2

Стороны картины — 18 и 35 сантиметров. Какова будет площадь стекла, накрывающего картину, если известно, что свободные бортики вокруг картины должны составлять по 3 сантиметра с каждой стороны?

Решение: S = 18 + 3 × 35 + 3 = 798 с м 2

Какова площадь круглой площади в центре города, если известно, что мужчина со средним шагом в 50 сантиметров дойдет от ее середины до края за 10 шагов?

Решение: S = π × 50 × 10 2 = 250000 π ( с м 2 ) = 25 π м 2 ≈ 78 , 5 м 2

Одно из стекол круглых очков разбилось. Мастер измерил диаметр сохранившегося стекла и пришел к выводу, что он равен 3 см. Какова должна быть площадь нового стекла, которое для очков вырежет мастер?

Решение: S = 1 4 × π × 3 2 = 2 , 25 π с м 2 ≈ 7 , 065 с м 2

Помещение в виде эллипса решили засыпать песком. На один м 2 уходит 1 мешок песка. Сколько потребуется песка на помещение с осями эллипса 20 и 36 м ?

Решение: S = π × a × b = 180 π м 2 ≈ 565 , 2 м 2
значит потребуется 566 мешков.

Как вычислить и обозначить площадь

Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».

Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела, а σ — площадь поперечного сечения провода в физике. Это основные символы, хотя могут быть и другие, например, в сфере сопротивления материалов, А — площадь сечения профиля.

Формулы расчета

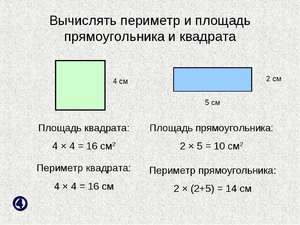
Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.

Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.

Треугольник

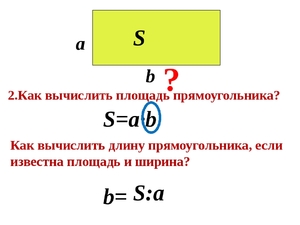
Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:

• S=√[p•(p-a)•(p-b)•(p-c)] — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника;
• S=a•h/2, где h — высота, опущенная на сторону a;
• S=a•b•(sin γ)/2, где γ — угол между сторонами a и b;
• S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты);
• S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника);
• S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).

Четырёхугольник

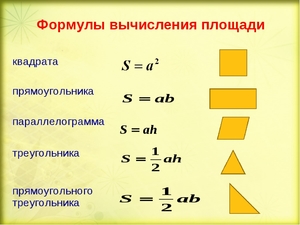
Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.

Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:

• S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции;
• S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали);
• S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ);
• S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр);
• S=a²=P²/16=d²/2, если ABCD — квадрат.

Многоугольник

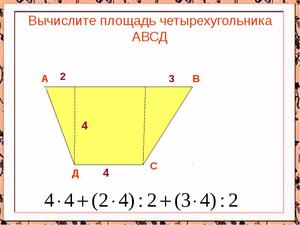
Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:

S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.

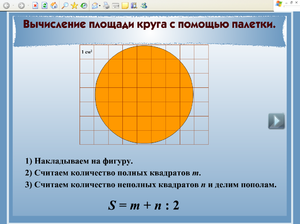
Круг — это совершенный многоугольник, имеющий бесконечное число сторон. Нам необходимо вычислить предел выражения справа в формуле площади многоугольника при числе сторон n, стремящемуся к бесконечности. В этом случае периметр многоугольника превратится в длину окружности радиуса R, которая будет границей нашего круга, и станет равен P=2•π•R. Подставим это выражение в указанную выше формулу. Мы получим:

Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:

Единицы измерения

Применяются системные и внесистемные единицы измерения. Системные единицы относятся к СИ (Система Интернациональная). Это квадратный метр (кв. метр, м²) и единицы, производные от него: мм², см², км².

В квадратных миллиметрах (мм²), например, измеряют площадь сечения проводов в электротехнике, в квадратных сантиметрах (см²) — сечения балки в строительной механике, в квадратных метрах (м²) — квартиры или дома, в квадратных километрах (км²) — территории в географии.

Однако иногда используются и внесистемные единицы измерения, такие, как: сотка, ар (а), гектар (га) и акр (ас). Приведём следующие соотношения:

Формулы площадей всех фигур в геометрии – примеры вычислений

Площадь — это одна из наиболее важных и неотъемлемых характеристик любой замкнутой геометрической фигуры, показывающая её размер. Она может измеряться в различных единицах: квадратных миллиметрах, сантиметрах, дециметрах, метрах и так далее. Это своеобразный аналог объёма трёхмерных фигур (шара, цилиндра, конуса и других). В геометрии разработаны формулы площадей. Их доказательством являются соответствующие теоремы. Существует общепринятое обозначение площади — буква S (от англ. square).

• Формулы для треугольников
• Площадь четырёхугольников
• Круг и эллипс

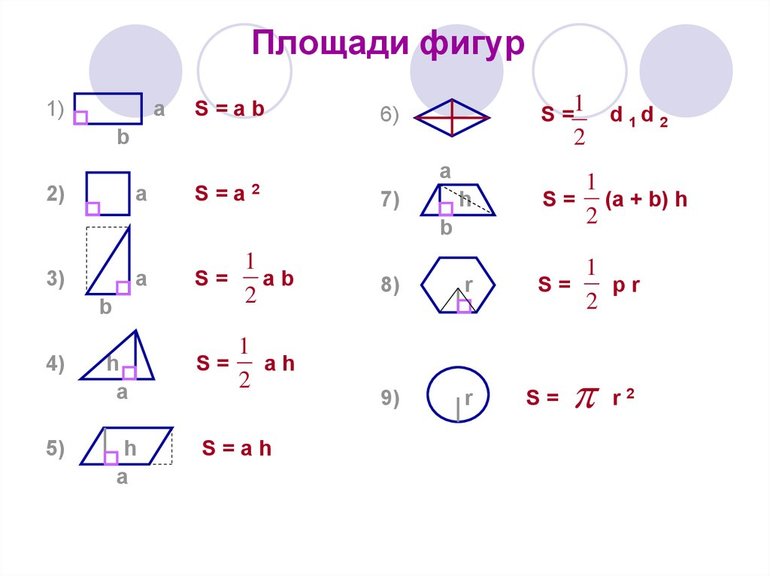
Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

• длина двух соприкасающихся в одной вершине сторон — a и b;
• градус угла, который образуют эти стороны.

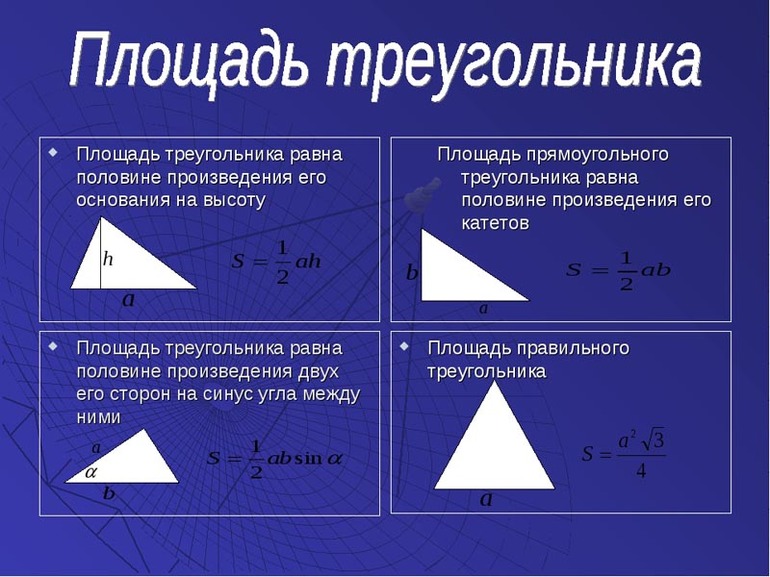
Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус ® окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

В любой треугольник: равносторонний и разносторонний, остроугольный и тупоугольный, в силу его геометрических свойств также может быть вписана окружность. В таком случае формула нахождения площади следующая: S = p * r. Буква p обозначает ½ периметра треугольника, r — это радиус окружности.

Площадь четырёхугольников

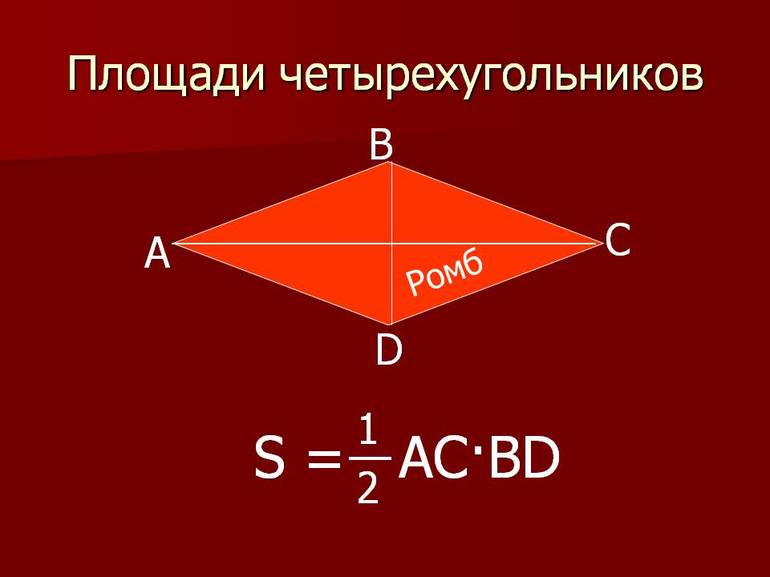
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.

К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.

Квадрат и прямоугольник

Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a 2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.

Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2 .

Для прямоугольника используется формула: S = a * b, где a, b — длина двух разных, имеющих общую вершину, сторон.

Параллелограмм, ромб и трапеция

Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.

Применяются три формулы площади параллелограмма:

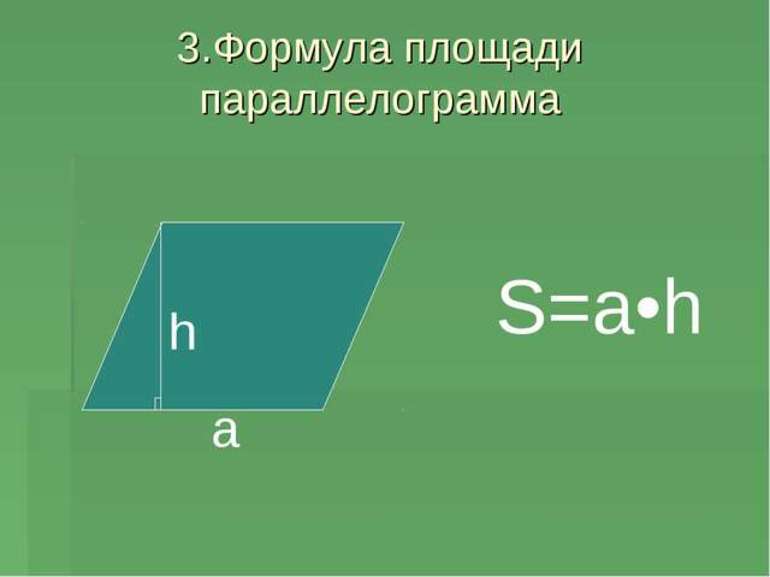
• Умножить сторону на высоту, перпендикулярную стороне: S = a * h.
• Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
• Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.

Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:

1. Умножить длину стороны на высоту.
2. Для ромба вторая формула площади параллелограмма преобразуется следующим образом: S = a 2 * sin γ. Поскольку все стороны у ромба равны (то есть a = b), то рассчитывается квадрат любой из них.
3. Площадь ромба рассчитать можно также, перемножив диагонали и разделив полученное число на два: S = ½ d (1) * d (2).

Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.

В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).

В этой формуле имеются следующие обозначения:

• буквы a, b — это основы трапеции,
• буквы c, d — стороны,
• p — полупериметр.

Выпуклый четырёхугольник

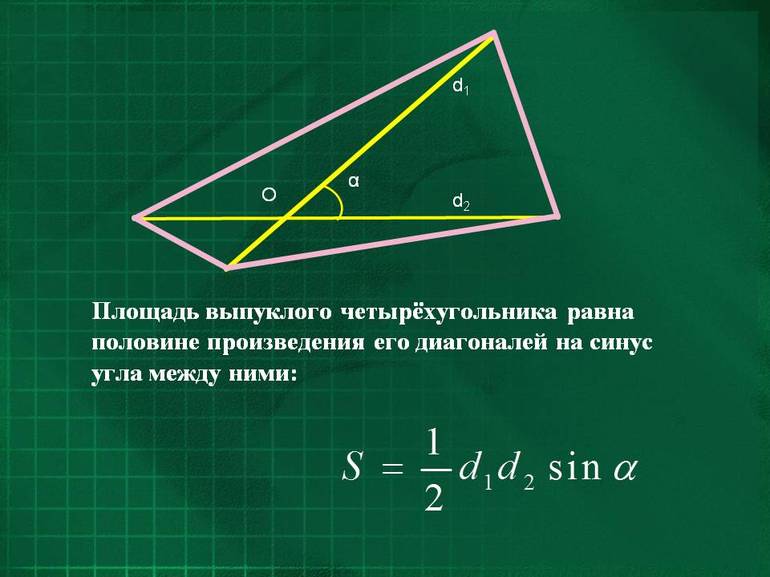
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.

Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.

В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:

• r — радиус окружности;
• p — ½ периметра четырёхугольника.

После чего полупериметр умножается на радиус. Это и будет площадь четырёхугольника. Формула выглядит так: S = p * r.

Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).

Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos 2 γ.

Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.

Круг и эллипс

Самое распространённое и широко применяемое правило определения площади круга — это умножение радиуса окружности в квадрате на число пи: S = π * r 2 .

Число пи, обозначаемое греческой буквой «π» – это математическая постоянная, которая является результатом деления длины окружности на диаметр. π – иррациональное число. Для расчётов признаётся его среднее значение, равное 3,14.

Вместо радиуса можно использовать диаметр окружности: диаметр возводится в квадрат, умножается на число π, результат делится на четыре. Формула выглядит так: S = (π * d 2 ) / 4.

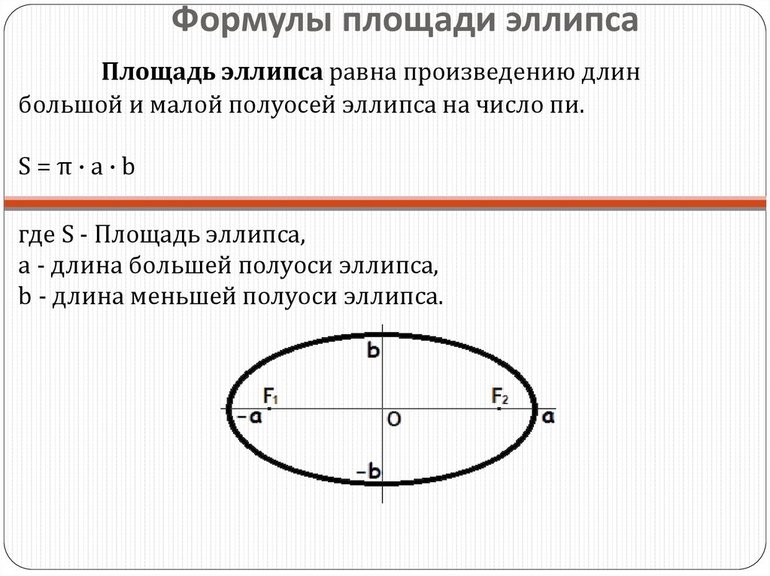
Для того чтобы посчитать площадь такой фигуры, как эллипс, необходимо провести две оси, то есть две линии, каждая из которых разделяет эллипс на две равные части, при этом сами линии перпендикулярны друг другу (образуют прямой угол). Точка пересечения разделяет каждую из осей напополам, образуя полуоси.

Площадь эллипса вычисляется как произведение трёх величин: числа π, длины большой полуоси (а) и длины малой полуоси (b): S = π * a * b. Для удобства расчёта площадей различных фигур также можно использовать специальные онлайн-калькуляторы.

Как посчитать площадь – какие способы пригодятся на стройке

С одной стороны нет ничего проще, как посчитать площадь любой поверхности (вертикальной, горизонтальной). Однако и здесь можно найти несколько нюансов и некоторые из них могут привести к трудностям. Разберём, что особенного может быть в вычислениях площади и рассмотрим несколько примеров. Прочтя этот материал, вы уже не будете плавать в этом вопросе. Заодно вспомните школьную программу с её формулами.

Почему не все так просто

Так вопрос, как рассчитать площадь любой поверхности может показаться смешным, ведь все мы учились в школе. Но не будем столь категоричными. Во-первых, со школьной скамьи многие из нас сошли со школьной скамьи очень давно. Во-вторых, не каждый раз в повседневной жизни приходится сталкиваться с необходимостью геометрических расчётов. И кое-что уже позабыто.

Ну и в третьих далеко не всегда поверхность имеет правильную форму. Тогда приходится изворачиваться, применяя более сложные приёмы расчёта. Это с квадратами и прямоугольниками все просто, но как быть в случае трапеции, треугольника и прочих сложных геометрических фигур?

Необходимость расчётов

Кто-то может задать и такой вопрос: «Собственно, а для чего потребуется рассчитать площадь?» Для этого есть определённые причины:

• Полученные данные позволят подобрать нужное количество строительных материалов, дабы не переплачивать.
• Рассчитав площадь, можно определить и объем помещения. А это уже главная характеристика, без которой не обойтись в случае выбора климатического оборудования, приборов отопления или системы вентиляции.
• Некоторые коммунальные услуги как раз учитывают площадь помещения.
• Выбор осветительных приборов, а точнее их количество, также зависит от этого рассчитываемого параметра.

Например, количество закупаемого ламината можно рассчитать, только зная площадь комнаты Источник bazazakonov.ru

С чего начинать

Самое время вспомнить школьную математику – чтобы рассчитать площадь, необходимы три параметра:

• Длина – обычно она бывает 4 либо 4,5 метра.
• Ширина – стандартное значение для большинства домов это 3 или 3,5 метра.
• Высота – в новостройках она обычно равна 2,5 метрам. А вот в постройках сталинской эпохи может составлять до 3 метров.

В решении задачи, как рассчитать площадь, не обойтись и без соответствующих инструментов:

• рулетки;
• строительного угольника;
• карандаша;
• калькулятора;
• строительного уровня.

Если планируются много писать, то вместо листка бумаги лучше взять блокнот либо тетрадь. Листики имеют свойство теряться, причём, когда нужно не всегда найдёшь их потом. Рулетка обязательно должна быть с фиксатором, иначе возникнуть сложности и процедура расчётов превратится в настоящее мучение.

Алгоритм проведения расчётов

Если все подготовлено, то можно переходить к самим расчётам. Если нужно вычислить площадь поверхности правильной формы, то здесь нет ничего сложного – эти формулы уж точно никто не позабудет.

Другое дело, когда стена, пол, потолок имеют сложные очертания. Здесь уже придётся сочетать различные приёмы. То есть поделить комнату на несколько блоков, после чего рассчитать площадь каждого из них. А далее от общей площади вычесть или прибавить их.

Вовсе не обязательно мерить длину стен строго вдоль плинтусов – замер можно проводить в любом удобном месте, если, скажем, мешает мебель. То есть выше, ниже, в середине, главное соблюсти при этом строгую параллель полу и потолку. Никаких диагоналей или наклонов! В противном случае расчёты будут неверными.

При возникновении трудностей можно всегда заручиться поддержкой кого-то из домашних.

Правильная геометрия

Каких-либо сложностей касательно того, как вычислить площадь, здесь нет. В случае простого прямоугольника достаточно замерить всего две стороны и высоту, ведь у такой фигуры противоположные стороны равны. Чтобы убедиться, что комната имеет правильные очертания, достаточно приложить к углам строительный угольник, правда не всегда удаётся получить чёткую картину.

Формула для расчёта прямоугольника известна каждому:

Кажется, что формулу площади прямоугольника забыть невозможно, хотя у некоторых получается и это Источник wezanu.ritobypus.ru.net

Такая формула актуальна для стен, потолка, пола, дверей, окон и прочих прямоугольных поверхностей. В случае запланированного ремонта важно получить чистые значения. Для этого следует от площади стены вычесть площадь дверей, окон. Общую площадь всей комнаты можно рассчитать по такой формуле – h(a⋅2+b⋅2). Где h – высота помещения.

С квадратом все ещё проще – достаточно замерить одну сторону и возвести её значение в квадрат.

Помещения с неправильными очертаниями

Но как посчитать площадь комнаты, если она имеет неправильную форму поверхностей? Здесь есть некоторые нюансы:

• Стены. В мансардной комнате стена может иметь форму трапеции или треугольника.
• Потолок. В тех же мансардных помещениях данная плоскость может быть под определённым углом. Также есть варианты с ломаной поверхностью, когда несколько плоскостей пересекаются межу собой.

Но ничего страшного здесь нет и не нужно углубляться в тригонометрию. Достаточно любую сложную поверхность стен или потолка визуально разделить на несколько простых плоскостей. После этого остаётся рассчитать площадь каждой фигуры и сложить их вместе.

Для облегчения ниже приведём несколько формул площадей, которые могут пригодиться:

Круг:

• S=π⋅R² – нужен только радиус.
• Сектор круга определятся так – S=0,5pr.

Параллелограмм:

• S=a⋅b⋅sin(α) – по двум сторонам и углу между ними.
• S=a⋅h – по высоте и основанию.

Треугольник:

• S=0,5⋅b⋅h – по основанию и высоте.
• S=0,5⋅ab⋅sin(α) – по сторонам и углу.
• S=√(p·(p-a)·(p-b)·(p-c)) – формула Герона по трем сторонам.

Трапеция:

• S=0,5⋅h⋅(a+b) – по высоте и основанию.
• S=m⋅h – по средней линии и высоте.

Эллипс:

• S = π⋅R1⋅R2 – по двум радиусам R1 и R2
• S=π⋅a⋅b – через полуоси a и b.

Обозначения: π – 3,14159 (всем известное число пи), R – радиус, a, b, c – стороны фигуры, p – полупериметр (для формулы Герона), h – высота, m – средняя линия.

Простое решение вопроса

Как высчитать квадратный метр стен, потолка или пола, если нет свободного времени, в особенности, когда имеешь дело со сложными фигурами, но есть интернет? В этом случае задача существенно упрощается. В сети можно найти кучу онлайн-калькуляторов, которые проведут все расчёты за несколько секунд. Все что нужно – это задать нужные параметры.

Для удобства все измерения указываются в разных единицах измерения, исходя из конкретных нужд. С их помощью любого такого калькулятора легко рассчитать не только площадь помещений, но и земельных участков. Кроме того, полученный результат можно преобразовать в любую другую нужную единицу измерения.

Видео описание

Для наглядности ниже подробная инструкция расчёта площади с разными примерами:

Краткий итог

Проблем с расчётом площади нужных поверхностей возникнуть не должно, если следовать правилу – от сложного к простому. Именно в этом и кроется успех больших достижений человечества. Не нужно все усложнять, достаточно проявить волю и смекалку и тогда любая задача, какой бы она ни была, будет решена.

Формулы площадей всех основных фигур

Зная диаметр или радиус круга, можно найти его площадь.

r – радиус круга

D – диаметр

Формула площади круга, (S):

2. Формула расчета площади треугольника

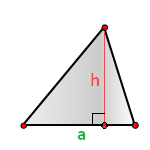
h – высота треугольника

a – основание

Площадь треугольника (S):

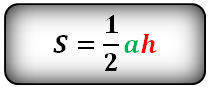
3. Площадь треугольника, формула Герона

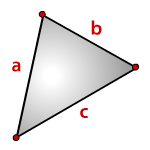
a , b , c , – стороны треугольника

p– полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

4. Площадь прямоугольного треугольника по катетам

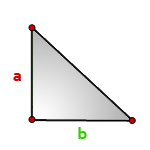
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.

a , b – катеты треугольника

Формула площади прямоугольного треугольника, (S):

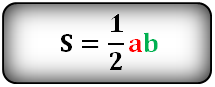
5. Как вычислить площадь равнобедренного треугольника ?

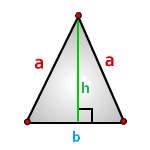
b – основание треугольника

a – равные стороны

h – высота

Формула площади треугольника через высоту h и основание b , ( S ):

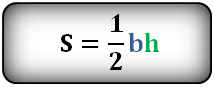
Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:

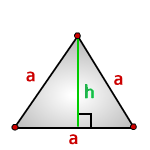
Формулы расчета, площади равностороннего треугольника.

a – сторона треугольника

h – высота

Площадь треугольника только через сторону a , (S):

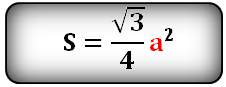
Площадь треугольника только через высоту h , ( S ):

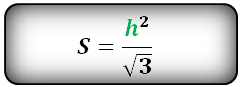
Площадь треугольника через сторону a и высоту h , (S):

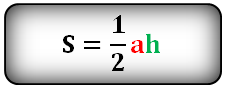
7. Найти площадь треугольника, угол и две стороны

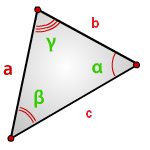
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.

a , b , c – стороны треугольника

α , β , γ – углы

Формулы площади треугольника, через две стороны и угол между ними, ( S ):

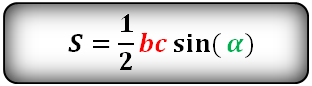
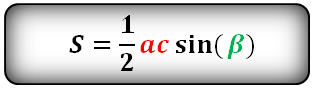
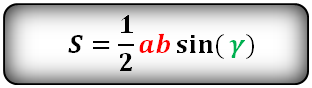
8. Площадь треугольника по стороне и двум углам, формула.

a , b , c – стороны треугольника

α , β , γ – противолежащие углы

Площадь треугольника через сторону и два угла (S):

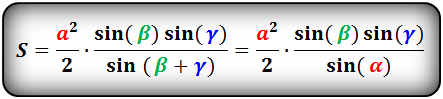
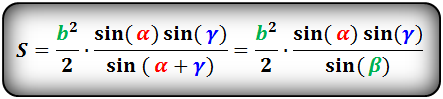
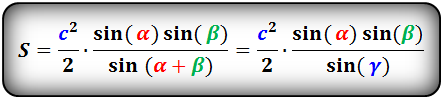
9. Формула расчета площади прямоугольника

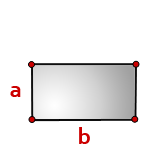
b – длина прямоугольника

a – ширина

Формула площади прямоугольника, (S):

10. Как рассчитать площадь квадрата через диагональ или сторону

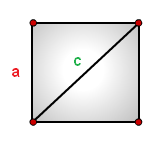
a – сторона квадрата

c – диагональ

Формула площади квадрата через сторону a , (S):

Формула площади квадрата через диагональ c , (S):

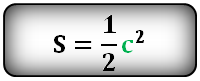
11. Формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b – стороны параллелограмма

α , β – углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

2. Формула площади параллелограмма через сторону и высоту

a, b – стороны параллелограмма

H _b – высота на сторону b

H _a – высота на сторону a

Формула площади через стороны и высоты параллелограмма, (S):

3. Формула площади параллелограмма через диагонали и угол между ними

D – большая диагональ

d – меньшая диагональ

α , β – углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , (S):

12. Площадь произвольной трапеции

1. Формула площади трапеции через основания и высоту

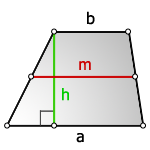
b – верхнее основание

a – нижнее основание

m – средняя линия

h – высота трапеции

Формула площади трапеции, (S):

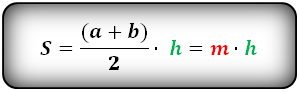
2. Формула площади трапеции через диагонали и угол между ними

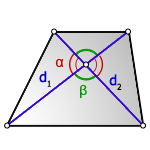
d ₁, d ₂ – диагонали трапеции

α , β – углы между диагоналями

Формула площади трапеции, (S):

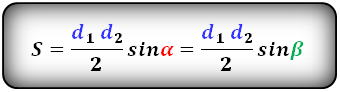
3. Формула площади трапеции через четыре стороны

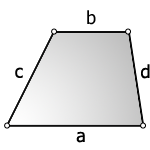
b – верхнее основание

a – нижнее основание

c, d – боковые стороны

Формула площади трапеции, (S):

13. Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание

a – нижнее основание

c – равные боковые стороны

α – угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности

D – диаметр вписанной окружности

O – центр вписанной окружности

H – высота трапеции

α , β – углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции

α , β – углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции

c – боковая сторона

α , β – углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание

a – нижнее основание

h – высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Площади фигур

Площадь фигуры — это аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Содержание:

Понятие площади

Площадь — это тоже величина. Каждой плоской геометрической фигуре соответствует своя площадь. У пространственных фигур тоже есть соответствующая им площадь, называемая площадью поверхности.

Площадь фигур мы будем обозначать буквой S. Запись читается как «площадь фигуры F».

Определение. Измерить площадь фигуры — это значит сравнить ее с площадью некоторой фигуры, принятой за единицу измерения площади.

Измерить площадь фигуры в Древней Греции означало построить квадрат, площадь которого равна площади данной фигуры. С тех пор всякое вычисление площади принято называть квадратурой.

Если за единицу длины принимается 1 мм, то единицей площади является 1 (квадратный миллиметр); при единице длины 1 см единицей площади является 1 (квадратный сантиметр). Если единицей измерения длины является 1 м, ему соответствует единица площади 1 (квадратный метр).

Любую площадь S можно выразить через единицу измерения площади в виде , где k — числовой множитель, который показывает, сколько раз единичный квадрат укладывается в данной фигуре.

Пусть, например, за единицу измерения площади принят квадратный сантиметр (т. е. ). Тогда запись означает, что площадь фигуры равна , т. е. в данной фигуре квадрат со стороной 1 см укладывается 15 раз.

Можно сфорулировать свойства измерения площади.

1. Всякий многоугольник F имеет площадь . Площадь является величиной, численное значение которой неотрицательно, т. е. для любой фигуры F.

Площадь фигуры зависит только от ее размеров и формы и не зависит от места расположения фигуры в пространстве. Это формулируется так.

2. Если две фигуры равны, то равны и их площади.

Пусть дана фигура F, которая является объединением двух фигур , причем эти фигуры пересекаются не более чем по конечному числу отрезков и точек. Тогда

Есть случаи, когда фигура является объединением двух других фигур, но данное равенство не выполняется. На рисунке 2.138 изображены два треугольника Фигура R — их объединение. В этом случае (при сложении площадь ромбовидной области в центре рисунка войдет в сумму дважды).

Еще одно свойство площади формулируется следующим образом.

3. За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения длины отрезка.

Для фигуры, разбитой на части, справедливо следующее свойство.

4. Если фигура разбита на части, то площадь фигуры равна сумме площадей частей фигуры.

Свойство измерения площади квадрата.

5. Площадь квадрата со стороной равна .

В геометрии различают фигуры равные и равновеликие.

Определение. Две фигуры называются равновеликими, если они имеют одинаковую площадь.

Площади прямоугольника и прямоугольного треугольника

Теорема 33. Площадь прямоугольника равна произведению его основания на высоту.

где — стороны прямоугольника.

Проведя диагональ АС прямоугольника ABCD (рис. 2.139), можно легко доказать, что она разбивает этот прямоугольник на два равных треугольника ABC и CDA, а тогда нетрудно доказать теорему 34.

Теорема 34. Площадь прямоугольного треугольника равна половине произведения его катетов (рис. 2.140):

где — катеты прямоугольного треугольника.

Площади треугольников

Теорема 35. Площадь треугольника равна половине произведения основания и высоты.

На рисунке 2.141 изображен треугольник ABC.

Есть еще одна формула для вычисления площади треугольника через его стороны. Эта формула носит имя древнегреческого математика Герона Александрийского (около I в.). Кроме этой формулы, есть еще так называемые ге-роновы треугольники — это треугольники, у которых целочисленные стороны и их площадь тоже есть целое число (примерами таких треугольников могут быть треугольники со сторонами 13, 14, 15 или 51, 52, 53).

Теорема 36 (формула Герона). Площадь треугольника равна

где — стороны треугольника, а р — его полупериметр, .

Существует формула площади треугольника, которая использует понятие синуса угла.

Теорема 37. Площадь треугольника равна половине произведения его сторон на синус угла между ними

где — стороны ААВС, а — угол между этими сторонами.

Площади четырехугольников и многоугольников

Для вывода формулы площади параллелограмма определим высоту параллелограмма.

Определение. Высотой параллелограмма называют отрезок перпендикуляра, проведенного из любой точки какой-нибудь стороны параллелограмма к прямой, содержащей противоположную сторону.

Высотой параллелограмма можно считать также и длину этого перпендикуляра. У параллелограмма две пары противоположных параллельных сторон и соответственно две высоты.

На рисунке 2.142 изображен параллелограмм ABCD, — его высоты. Заметим, что основания высот параллелограмма могут попасть и на продолжение одной из сторон (рис. 2.143).

Теорема 38. Площадь параллелограмма равна произведению его стороны и проведенной к ней высоты.

ABCD — параллелограмм, AD = ВС = , AM = CN = h (рис. 2.144).

Для вывода формулы площади еще одного четырехугольника — трапеции определяется понятие высоты трапеции.

Определение. Высотой трапеции называют отрезок перпендикуляра, проведенного из какой-либо точки основания трапеции к прямой, содержащей другое основание.

Высотой можно также считать длину этого перпендикуляра. На рисунке 2.145 ВМ — высота трапеции ABCD.

Теорема 39. Площадь трапеции равна произведению полусуммы оснований и высоты, т. е. если и — основания трапеции, h — высота и S — площадь трапеции, то

Чтобы вычислить площадь произвольного многоугольника, можно разбить его на треугольники, не имеющие общих внутренних точек, и найти сумму их площадей.

Такое разбиение выпуклого многоугольника можно осуществить, проведя, например, диагонали из одной его вершины (рис. 2.146). Иногда удобно пользоваться другими разбиениями (рис. 2.147, 2.148).

Пример:

Через середину основания треугольника проведены прямые, параллельные боковым сторонам. Докажите, что полученный таким образом четырехугольник — параллелограмм и что его площадь равна половине площади треугольника.

Решение:

Из условия задачи имеем:

1.

2. AD = DC. (рис. 2.149)

3. DE || ВС, DF || АВ.

4. Надо доказать, что BEDF — параллелограмм и что

5. Так как DE || ВС и DF || АВ, то BEDF — параллелограмм (2, определение параллелограмма).

Нужно установить связь между площадью параллелограмма и треугольника. Для этого удобно параллелограмм разбить на треугольники.

6. Соединим точки В и D и рассмотрим полученные треугольники (построение) (рис. 2.150).

7. равны (BD — общая сторона, и , как углы внутренние накрест лежащие при параллельных прямых (1, 2, 3, признак равенства треугольников по сторонам и двум прилежащим углам).

8. Эти треугольники и равновелики.

9. Треугольники BFD и CFD также равновелики между собой (хотя в общем случае они не равны), так как BF = FC (DF — средняя линия), т. е. основания их равны и они имеют одинаковую высоту, так как вершина D у них общая.

10. Аналогично равновелики между собой и

11. следовательно, площади и параллелограмма BEDF можно записать так: а (8, 10, свойства площадей).

12. (11).

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

Смотрите также дополнительные лекции по предмету “Математика”:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.