Что такое Сумма Разрядных Слагаемых

Что такое разрядные слагаемые?

Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.

В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.

Сумма разрядных слагаемых натурального числа, в виде суммы разрядных слагаемых

Каким образом можно разложить число по разрядам?

Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах. Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.

Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5, 10, 400, 200относятся к данной категории, а числа 144, 321, 5 540, 16 441 – не относятся.

Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля. Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.

Сумма разрядных слагаемых натурального числа равна этому числу. Перейдем к понятию разрядных слагаемых.

Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.

Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.

Как раскладывать числа?

Если вы возьмем, например, число 58, то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4тысячам и 4 сотням.

Можно представить эти числа в виде равенств – 50+8=58 и 134 400=100 000+30 000+4 000+400. В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых. Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.

Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25=20+5. А вот сумма 17+8 не является суммой разрядных слагаемых числа 25, так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.

Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.

Как найти натуральное число, если известна сумма разрядных слагаемых?

Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.

Например, сумма 200+30+8 разложено по разрядам числа 238, а сумма 3 000 000+20 000+2 000+500 соответствует натуральному числу 3 022 500. Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.

Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.

Пример 1

Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000+40 000+50+5. Перейдем к решению. Необходимо записать числа 200 000, 40 000, 50 и 5 для сложения в столбик:

Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.

Выполнив сложение, мы получим натуральное число 240 055, сумма разрядных слагаемых которого имеет вид 200 000+40 000+50+5. Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.

Пример 2

Разложение по разрядам числа 725 будет представлено как 725=700+20+5, а сумму разрядных слагаемых 700+20+5 можно представить как (700+20)+5=720+5 или 700+(20+5)=700+25, или (700+5)+20=705+20. Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.

Пример 3

Выполним вычитание чисел 5 677 и 670. Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677=5 000+600+70+7. Выполнив действие, мы можем сделать вывод, что. сумме (5 000+7)+(600+70)=5 007+670. Тогда 5 677−670=(5 007+670)−670=5 007+(670−670)=5 007+0=5 007.

Что такое разрядные слагаемые

Разрядные слагаемые – это сумма чисел с разной разрядностью. Возьмем на примере, число 86. Разложим данное число на десятки и единицы. Получаем: 86 = 80 + 6 = 8 * 10 + 6 * 1. Отсюда видим, что число 86 состоит из 8 десятков и 6 единиц. Это и есть разрядные слагаемые.

Числа 1, 10, 100, 1000 и так далее – это разрядные единицы. Запишем разделение разрядных слагаемых:

Числа от 1 и до 9 – это единицы;
Числа 10, 20, … , 90 – это десятки;
Число 100, 200, … , 900 – это сотни и так далее.

Любое натуральное число можно разделить на разрядные слагаемые и записать в виде суммы. Примеры разрядных слагаемых:

892 = 800 + 90 + 2;
1695 = 1000 + 600 + 90 + 5;
45 = 40 + 5.

Рассмотрим пример определения разрядных слагаемых числа 92586

Сначала, разложим число 92586 на разрядные слагаемые и получим:

92 586 = 90000 + 2000 + 500 + 80 + 6 = 9 * 10 000 + 2 * 1 000 + 5 * 100 + 8 * 10 + 6 * 1.

Запишем, из чего состоит число 92 586:

Из 9 десятков тысяч 9 * 10 000;
Из 2 единиц тысяч 2 * 1000;
Из 5 сотен 5 * 100;
Из 8 десятков 8 * 10;
Из 6 единиц 6 * 1.

Сделаем вывод, что любое число можно разделить на разрядные слагаемые. Разрядные слагаемые помогают при решении более сложных примеров и задач.

Разрядное слагаемое — это любое натуральное многозначное число, которое можно представить в виде суммы разрядных слагаемых. Разложить число на разрядные слагаемые значит разделить число на разряды: единицы, десятки, сотни, тысячи, десятки тысяч и так далее.

Примеры разложения чисел на разрядные слагаемые:123 = 100 + 20 + 3, где 100 — сотни, 20 — десятки, а 3 — единицы.Более сложный пример с большим числом разрядов:16 458 = 10 000 + 6 000 + 400 + 50 + 8, здесь 10 000 — десятки тысяч, 6 000 — тысячи, 400 — сотни, 50 — десятки, 8 — единицы.

Сумма разрядных слагаемых

Уметь быстро решать примеры в уме — навык полезный. Конечно, под рукой всегда есть смартфон, но куда приятнее и эффективнее — вычислять самостоятельно и гордиться собой. Есть много фишек, чтобы упростить устный счет: разрядные слагаемые — одна из них.

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сумма разрядных слагаемых

Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:

Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.

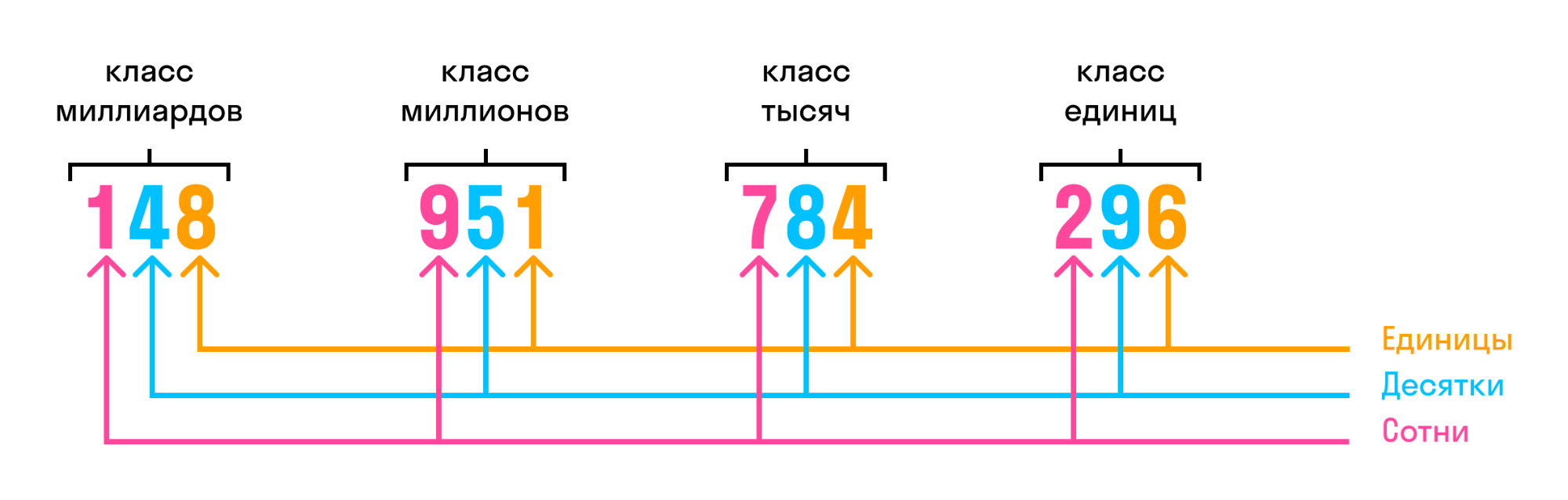
Названия классов многозначных чисел:

первый — класс единиц,
второй — класс тысяч,
третий — класс миллионов,
четвёртый — класс миллиардов,
пятый — класс триллионов,
шестой — класс квадриллионов,
седьмой — класс квинтиллионов,
восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

10 единиц = 1 десяток;
10 десятков = 1 сотня;
10 сотен = 1 тысяча;
10 тысяч = 1 десяток тысяч;
10 десятков тысяч = 1 сотня тысяч;
10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.

Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

шести единиц миллионов (6 * 1 000 000);
пяти десятков тысяч (5 * 10 000);
семи единиц тысяч (7 * 1000);
трех сотен (3 * 100);
восьми десятков (8 * 10);
шести единиц (6).

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц в числе 5 068 252.

1. Определяем сколько всего единиц в числе.

2. Определяем количество десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).

4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).

5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.

7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Примеры

Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.

Представьте в виде суммы разрядных слагаемых:

84 610
84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
84 610 = 80 000 + 4 000 + 600 + 10.
45 317
45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
45 317 = 40 000 + 5 000 + 300 + 17.
56 789
56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
56 789 = 50 000 + 6 000 + 700 + 80 + 9.
345 677
345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
687 543
687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
877 589
877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.

Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.

Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.

4 895 634
4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
8 675 349
8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
77 897 125
77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
656 734 212
656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.

Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.

Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.

Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.

Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.

Разряды чисел.

Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.

Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.

Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.

Такой разбор числа называется разрядным составом числа.

Классы.

Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.

Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.

Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.

Таблица разрядов и классов.

Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:

13 миллиардов 562 миллионов 6 тысяч 891.

Сумма разрядных слагаемых.

Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.

4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать

4062=4 ⋅1000+0 ⋅100+6 ⋅10+2

Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0

Вопросы по теме:

Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.

Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.

Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.

Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.

Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.

Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)

Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)

Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.

Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.

Примеры на задачи.

Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)

Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)

Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.

Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.

Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6

Сумма разрядных слагаемых натурального числа

Каким образом можно разложить число по разрядам?

Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.

Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа 5 , 10 , 400 , 200 относятся к данной категории, а числа 144 , 321 , 5 540 , 16 441 – не относятся.

Количество разрядных слагаемых у представленного числа равняется тому числу, сколько цифр, отличных от нуля, содержится в записи. Если представить число 61 как сумму разрядных слагаемых, так как 6 и 1 отличаются от . Если разложить число 55050 как сумму разрядных слагаемых, то оно представлено как сумма 3 слагаемых. Три пятерки, представленные в записи, отличны от нуля.

Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.

Сумма разрядных слагаемых натурального числа равна этому числу.

Перейдем к понятию разрядных слагаемых.

Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.

Как раскладывать числа?

Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее. Если вы возьмем, например, число 58 , то может отметить, что он отвечает 5 десяткам и 8 единицам. Число 134 400 соответствует 1 сотне тысяч, 3 десяткам тысяч, 4 тысячам и 4 сотням. Можно представить эти числа в виде равенств – 50 + 8 = 58 и 134 400 = 100 000 + 30 000 + 4 000 + 400 . В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых.

Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.

Приведем еще один пример. Представим натуральное число 25 в виде суммы разрядных слагаемых. Число 25 соответствует 2 десяткам и 5 единицам, поэтому 25 = 20 + 5 . А вот сумма 17 + 8 не является суммой разрядных слагаемых числа 25 , так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.

Как найти натуральное число, если известна сумма разрядных слагаемых?

Например, сумма 200 + 30 + 8 разложено по разрядам числа 238 , а сумма 3 000 000 + 20 000 + 2 000 + 500 соответствует натуральному числу 3 022 500 . Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.

Необходимо определить исходное число, если известна сумма разрядных слагаемых 200 000 + 40 000 + 50 + 5 . Перейдем к решению. Необходимо записать числа 200 000 , 40 000 , 50 и 5 для сложения в столбик:

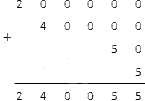
Получаем:

Выполнив сложение, мы получим натуральное число 240 055 , сумма разрядных слагаемых которого имеет вид 200 000 + 40 000 + 50 + 5 .

Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.

Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.

Выполним вычитание чисел 5 677 и 670 . Для начала представим число 5677 в виде суммы разрядных слагаемых: 5 677 = 5 000 + 600 + 70 + 7 . Выполнив действие, мы можем сделать вывод, что. сумме ( 5 000 + 7 ) + ( 600 + 70 ) = 5 007 + 670 . Тогда 5 677 − 670 = ( 5 007 + 670 ) − 670 = 5 007 + ( 670 − 670 ) = 5 007 + 0 = 5 007 .

Разрядные слагаемые в математике

Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.
[block >

Натуральные числа

При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.

Разряды и классы чисел

Разряды

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

Первый — единиц, содержит до 3 знаков:

200 + 10 +3 = 213.

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

Сорок пять состоит из четырёх десятков и пяти простых единиц.
[block > Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:

шестьсот тысяч;
семьдесят тысяч;
девять тысяч;
восемьсот;
десять;
два;

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

Это число содержит девять разрядных слагаемых:

800 миллионов;
80 миллионов;
7 миллионов;
200 тысяч;
10 тысяч;
3 тысячи;
6 сотен;
4 десятка;
4 единицы;

7 891 234.

В этом числе нет слагаемых выше 7 разряда.
[block > Четвёртый — миллиардов, от 10 до 12 цифр:

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

единицы сотен миллиардов;
единицы десятков миллиардов;
единицы миллиардов;
сотен миллионов;
десятков миллионов;
миллионов;
сотен тысяч;
десятков тысяч;
тысяч;
простые сотни;
простые десятки;
простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.
[block > При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

487 789 654 427 241.

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

321 546 818 492 395 953;

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31 , чем приписывать тридцать один ноль к единице.
[block >
[block > [block >

Сумма разрядных слагаемых

Для всех тех кто хочет научится быстро считать и уметь быстро решать примеры в уме мы дадим очень полезный навык. Для того чтобы ваш счет был не только на телефоне или калькуляторе, вам может пригодится ряд советов из этой статьи. Вы сможете быстро считать прямо в уме.

О чем эта статья:

Сумма разрядных слагаемых
Разряды и классы чисел
Примеры

Сумма разрядных слагаемых

Число 35 состоит из 3 десятков и 5 единиц

35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.

30 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 86 состоит из 8 десятков и 6 единиц

86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86

80 — разрядное слагаемое; 5 — разрядное слагаемое.

Число 356 состоит из 3 сотен, 5 десятков и 6 единиц

356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.

300, 50, 6 — разрядные слагаемые.

Разряды и классы чисел

Названия классов многозначных чисел:

первый — класс единиц,
второй — класс тысяч,
третий — класс миллионов,
четвёртый — класс миллиардов,
пятый — класс триллионов,
шестой — класс квадриллионов,
седьмой — класс квинтиллионов,
восьмой — класс секстиллионов.

345 466 129 350 вместо 345466129350

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.

Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.

10 единиц = 1 десяток;
10 десятков = 1 сотня;
10 сотен = 1 тысяча;
10 тысяч = 1 десяток тысяч;
10 десятков тысяч = 1 сотня тысяч;
10 сотен тысяч = 1 миллион.

Например, нужно сказать, сколько сотен в числе 5689.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

шести единиц миллионов (6 * 1 000 000);
пяти десятков тысяч (5 * 10 000);
семи единиц тысяч (7 * 1000);
трех сотен (3 * 100);
восьми десятков (8 * 10);
шести единиц (6).

Определите, сколько единиц в числе 5 068 252.

Примеры

Представьте в виде суммы разрядных слагаемых:

1. 84 610
  84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
  84 610 = 80 000 + 4 000 + 600 + 10.
1. 1. 45 317
    45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
    45 317 = 40 000 + 5 000 + 300 + 17.
  1. 1. 56 789
      56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
      56 789 = 50 000 + 6 000 + 700 + 80 + 9.
    1. 1. 345 677
        345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
        345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7.
      1. 687 543
        687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
        687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3.
        
        877 589
        877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
        877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.
        
        Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
        
        Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
        
        4 895 634
        4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
        4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4.
        
        8 675 349
        8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
        8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9.
        
        77 897 125
        77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
        77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5.
        
        656 734 212
        656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
        656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.
        
        Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
        
        Копирование информации с сайта greednews.su разрешено только при использовании активной гипер ссылки на новость, спасибо за то что цените наши авторские права!
        
        Похожие записи:
        
        Что такое разность чисел в математике: определение, правила нахождения
        
        Атмосферный фронт: что это, признаки теплого и холодного фронта, схема циклона и антициклона, характеристики движения
        
        Слитное или раздельное написание оборотов «несмотря на» и «не смотря на» с примерами
        
        Слово торты, где правильно ставить ударение: на первый или второй слог по правилам русского языка