Основные правила и свойства умножения вектора на число и их применение на стандартных заданиях

§ 3. Умножение вектора на число

Прежде чем ввести ещё одно действие — умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй автомобиль движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т. е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля.

Если мы изобразим скорость первого автомобиля вектором (рис. 260, а), то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора , а длина в два раза больше, и обозначить этот вектор 2. Скорость третьего автомобиля изобразится вектором, противоположным вектору 2, т. е. вектором -2 (см. рис. 260, а). Естественно считать, что вектор 2 получается умножением вектора на число 2, а вектор -2 получается умножением вектора на число -2. Этот пример подсказывает, каким образом следует ввести умножение вектора на число.

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна причём векторы и сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор.

Произведение вектора на число k обозначается так: На рисунке 260, б изображены вектор и векторы

Из определения произведения вектора на число непосредственно следует, что:

1) произведение любого вектора на число нуль есть нулевой вектор;

Умножение вектора на число обладает следующими основными свойствами:

1 0 . (сочетательный закон).

2 0 . (первый распределительный закон).

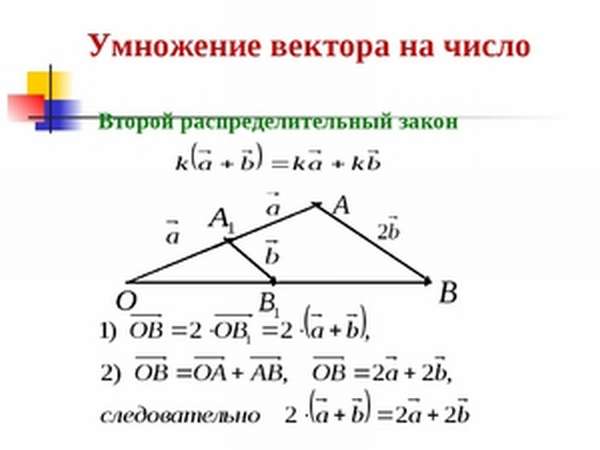
Рисунок 261 иллюстрирует сочетательный закон. На этом рисунке представлен случай, когда k = 2, l = 3.

Рисунок 262 иллюстрирует первый распределительный закон. Этот рисунок соответствует случаю, когда k = 3, l = 2.

Рисунок 263 иллюстрирует второй распределительный закон. На этом рисунке треугольники ОАВ и ОА₁В₁ подобны с коэффициентом подобия k, поэтому . С другой стороны, . Таким образом, .

Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение можно преобразовать так:

Применение векторов к решению задач

Векторы могут использоваться для решения геометрических задач и доказательства теорем. Приведём примеры. Рассмотрим сначала вспомогательную задачу.

Точка С — середина отрезка АВ, а О — произвольная точка плоскости (рис. 264). Доказать, что

По правилу треугольника . Складывая эти равенства, получаем: . Так как точка С — середина отрезка АВ, то Таким образом, или

Доказать, что прямая, проведённая через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

Пусть ABCD — данная трапеция, М и N — середины оснований ВС и AD, а О — точка пересечения прямых АВ и CD (рис. 265). Докажем, что точка О лежит на прямой MN.

Треугольники OAD и ОВС подобны по первому признаку подобия треугольников (докажите это), поэтому

Точка М — середина отрезка ВС, поэтому

Подставив в это равенство выражения (1) для

Отсюда следует, что векторы коллинеарны, и, значит, точка О лежит на прямой MN.

Средняя линия трапеции

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. Докажем теорему о средней линии трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Пусть MN — средняя линия трапеции ABCD (рис. 266). Докажем, что

По правилу многоугольника Сложив эти равенства, получим:

Но М и N — середины сторон АВ и CD, поэтому и Следовательно, откуда

Так как векторы сонаправлены, то векторы также сонаправлены, а длина вектора равна AD + BC. Отсюда следует, что и

Практические задания

775. Начертите два неколлинеарных вектора начала которых не совпадают, и отметьте какую-нибудь точку О. От точки О отложите векторы, равные

776. Начертите два неколлинеарных вектора и постройте векторы:

Выполните задания а) — е) для двух коллинеарных ненулевых векторов .

777. Начертите два неколлинеарных вектора начала которых не совпадают. Постройте векторы

778. Начертите попарно неколлинеарные векторы Постройте векторы:

Задачи

779. Дан вектор Как направлен каждый из векторов по отношению к вектору Выразите длины этих векторов через .

780Докажите, что для любого вектора справедливы равенства:

781. Пусть Выразите через векторы:

782. В параллелограмме ABCD точка Е — середина стороны AD, точка G — середина стороны ВС. Выразите векторы через векторы

783. Точка М лежит на стороне ВС параллелограмма ABCD, причём ВМ : МС = 3 : 1. Выразите векторы через векторы

784. В параллелограмме ABCD диагонали пересекаются в точке О, а М — такая точка на стороне AD, что Выразите через векторы следующие векторы:

785. Точки М и N — середины диагоналей АС и BD четырёхугольника ABCD. Докажите, что

786. Отрезки АА₁, ВВ₁ и СС₁ — медианы треугольника АВС. Выразите векторы через векторы

787. Точка О — середина медианы EG треугольника DEF. Выразите вектор через векторы

Применение векторов к решению задач

788. Дан произвольный треугольник АВС. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.

Пусть АА₁, ВВ₁, СС₁ — медианы треугольника АВС. Тогда

(см. задачу 1, п. 87). Сложив эти равенства, получим

Отсюда следует, что если мы построим сумму векторов по правилу многоугольника (п. 84), то получим треугольник, удовлетворяющий условиям задачи (треугольник MNP на рисунке 267).

789. На сторонах треугольника АВС построены параллелограммы АВВ₁А₂, ВСС₁В₂, АСС₂А₁. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А₁А₂, В₁В₂ и С₁С₂.

790. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен полуразности оснований.

791. Докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырёхугольника, точкой пересечения делятся пополам.

792. Докажите теорему о средней линии треугольника (п. 64).

Средняя линия трапеции

793. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции.

794. Сторона АВ треугольника АВС разделена на четыре равные части и через точки деления проведены прямые, параллельные стороне ВС. Стороны АВ и АС треугольника отсекают на этих параллельных прямых три отрезка, наименьший из которых равен 3,4 см. Найдите два других отрезка.

795. Найдите диаметр окружности, если его концы удалены от некоторой касательной на 18 см и 12 см.

796. Из концов диаметра CD данной окружности проведены перпендикуляры СС, и DDl к касательной, не перпендикулярной к диаметру CD. Найдите DDU если ССг = 11 см, a CD = 27 см.

797. Докажите, что средняя линия трапеции проходит через середины диагоналей.

798. Боковая сторона равнобедренной трапеции равна 48 см, а средняя линия делится диагональю на два отрезка, равные 11 см и 35 см. Найдите углы трапеции.

799. Дана равнобедренная трапеция ABCD. Перпендикуляр, проведённый из вершины В к большему основанию AD, делит это основание на два отрезка, больший из которых равен 7 см. Найдите среднюю линию трапеции.

Особенности и правила умножения вектора на число

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

• Основные понятия и определения
• Правила умножения вектора на число
• Алгебраический и геометрический смысл действия
• Формулы умножения
• Возможные действия с векторами

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

1. Постоянная — любое обычное число, которое может принимать определённые фиксированные значения, быть положительным, отрицательным или нулевым. Обозначать будем латинской буквой С (от греческого слова constanta, то есть постоянная).
2. Вектор — участок прямой, ограниченный двумя точками и имеющий заданное направление. Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
3. Вектора называются параллельными (коллинеарными), если они лежат на коллинеарных прямых или на одной прямой.
4. Нулевым вектором называется такой, у которого конец и начало совпадают. Называется нуль-вектор и обозначается (0).
5. Координатами (АВ) называются числа, равные его протяжённости относительно каждой из оси координат в Декартовой системе. Они находятся вычитанием из координат конца вектора координат его начала. Знак минус перед этим числом означает, что вектор направлен против направления данной оси.
6. Модулем (АВ) называется длина отрезка АВ.
7. Квадратный корень из числа или выражения условимся обозначать латинским буквосочетанием SQRT.
8. (АВ) с координатами (x, y, z) будем обозначать как (АВ) (x, y, z).

Это интересно: Как найти разность чисел в математике?

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

1. Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
2. Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
3. Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
4. Для умножения (АВ) (x, y, z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x, С*y, С*z).

Интересно знать: Модуль числа в математике.

Алгебраический и геометрический смысл действия

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

1. Геометрический смысл: (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.
2. Алгебраический смысл: (АВ) (x, y, z)*С — это новый (А1В1) с координатами равными (С*x, С*y, С*z).
3. Физический смысл: уменьшение или увеличение в С раз силы действующей на тело или материальную точку.

Это интересно: как разложить на множители квадратный трехчлен?

Формулы умножения

При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

• С*(АВ) (x, y, z) = (А1В1) (С*x, С*y, С*z).
• 0*(АВ) = (0).

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57,63,28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57,63,28) = (А1В1) (10*57,10*63,10*28) = (А1В1) (570,630,280).

Вторую задачу возьмём аналогичную: как изменится сила, действующая на материальное тело, описываемая (АВ) (46,59,-43) при её увеличении в -0,5 раза.

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46,59,-43) = (А1В1) (-0,5*46,-0,5*59,-0,5*(-43)) = (А1В1) (-23,-29,5,21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

• 33*(CD) (11,10) = (C1D1) (33*11,33*10) = (C1D1) (363,330).
• -0,2*(АВ) (-0,3,25) = (А1В1) (-0,2*(-0,3), -0,2*25) = (А1В1) (0,06, -5).
• 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
• 0*(АВ) (65,-87) = (0).

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

• модуль (АВ) (3,4) = SQRT (3 2+ 4 2) = SQRT (9 + 16) = SQRT25 = 5.

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону.

Умножение вектора на число

Определение 6. Произведением вектора на вещественное число называется вектор , коллинеарный вектору , имеющий длину и сонаправленный с вектором , если , и противонаправленный с вектором , если . Произведением вектора на число обозначается или .

На рис. 6 – рис. 9 показаны пары векторы и , и , и , и

Противоположный вектор можно рассматривать как результат умножения вектора на число :

Отметим некоторые свойства умножения вектора на число.

1. – закон коммутативности.

2. – закон ассоциативности.

3. – закон дистрибутивности.

4. – закон дистрибутивности.

Теорема 1. Для коллинеарности векторов и , необходимо и достаточно существование числа такого, что выполняется хотя бы одно из равенств или .

Сумма векторов

Определение 7. Суммой векторов и называется вектор , вычисляемый как диагональ параллелограмма, построенного на этих векторах, имеющая с ними общее начало (рис. 10). Сумма векторов и обозначается .

Отметим некоторые свойства суммы векторов.

1. – закон коммутативности.

2. – закон ассоциативности.

Разность векторов

Определение 8. Разностью векторов и называется вектор, сумма которого с вектором равна вектору . Разность можно определить как сумму вектора с вектором, противоположным к вектору : .

Разность векторов и можно вычислить по правилу параллелограмма, как диагональ этого параллелограмма, исходящей из конца вектора (рис. 11).

Сумма и разность векторов определялись по правилу параллелограмма. Можно эти две операции определить по правилу треугольника. Для определения суммы , следует параллельным переносом начало вектора совмещать с концом вектора . Для определения разности , следует концы этих векторов.

Числовая ось

Числовой осью (числовой прямой) называется любая прямая, если:

1) на ней выбрана некоторая точка, называемая началом (центром) и обозначаемая ;

2) любое из двух направлений, называемое положительным направлением и обозначаемое стрелкой;

3) некоторый отрезок, называемый единичным отрезком (масштабом).

Каждому вещественному числу на числовой прямой соответствует единственная точка на числовой оси:

1) положительное число изображается точкой, расположенной на оси на расстоянии по направлению стрелки;

2) отрицательное число изображается точкой, расположенной на оси на расстоянии против направления стрелки;

3) нулевое число изображается началом оси.

Имеет место и обратное соответствие: каждой точке на числовой оси соответствует единственное вещественное число.

Пусть точке числовой оси соответствует число . Координатой точки называется число и обозначается .

Единичный вектор

Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором.

Пусть задан вектор . Обозначим через единичный вектор, сонаправленный с вектором , называемый ортом этого вектора . Из определения умножения вектора на число следует, что

Для каждой числовой оси определен единичный вектор , с началом в точке ( – центр числовой оси) и концом в точке с координатой (рис. 12). Направление единичного вектора совпадает с положительным направлением числовой оси .

Угол между векторами

Определение 10. Пусть векторы и имеют общее начало. Углом между векторами и называется наименьший угол , на который нужно повернуть один из этих векторов до совпадения с другим (рис. 13). Под термином совпадение понимается, что векторы и окажутся сонаправленными. Угол между векторами и обозначают .

Из определения вытекает, что угол между произвольными векторами содержится в промежутке: .

Определение 11. Пусть начало вектора находится в центре числовой оси . Углом между вектором и осью называется угол между вектором и единичным вектором оси (рис. 14).

32. Операция умножения вектора на число и ее свойства

Произведение вектора A на число l обозначается символом L A. Числа называют также Скалярными величинами или Скалярами.

Теорема 8. Вектора A ≠ Коллинеарен вектору B тогда и только тогда, когда найдется такое число, что B = L A.

Доказательство. Если, то по определения 13 следует, что векторы коллинеарны. Обратно, пусть вектора коллинеарны. Тогда, полагая L = ±|B|/|A|, где стоит знак “+”, если A­­B, стоит знак “-“, если A­¯B, по определению 13 получим B = L A.

Теорема 9. Для любых векторов A, B и для любых чисел l, m Справедливы свойства:

1) l(m A) = (lm) A – Смешенный ассоциативный закон;

2) (l + m) A = l A+ m A – Дистрибутивный закон;

3) l (A + B) = l A + l B – Дистрибутивный закон;

4) 1 A = A – Свойство умножения на единицу.

Доказательство. 1. Если векторы A или B равны Или числа m равны нулю, то равенства 1-3 теоремы почти очевидны (проверте их). Также по определению равенства векторов проверяется равенство 4. Поэтому дальше будем считать, что A ≠ , B ≠ , lm ≠ 0.

1. Длины векторов l(m A), (lm) A равны |l||m| |A|, и поэтому равны между собой. Далее оба эти вектора коллинеарны вектору A. Если числа l и m одного знака, то направление векторов l(m A), (lm) A совпадает с направлением вектора A. Если числа l и m противоположных знаков, то эти векторы противоположны вектору A. Отсюда по определению векторы l(m A), (lm) A равны.

2. Если числа l и m одного знака, то векторы (l + m) A, l A, m A сонаправлены и |l A+m A| = |l A|+|m A|= |l ||A| + | m|| A| = (| l | + | m | )| A|.

Так как в этом случае |l + m | = | l | + | m |, то |(l + m) A| = || l A + m A|.

Отсюда, по определению равенства векторов (l + m) A = l A + m A.

Случай, когда числа l и m противоположного знака рассмотрите самостоятельно.

3. Если векторы A и B коллинеарны, то по теореме 8 его можно представить в виде B = m A. Тогда по свойствам 1, 2 и 4 имеем

L (A + B) = l (1A + m A) = l (1A) + l (m A) =l A + l (m A) = l A + l B.

Если векторы A и B неколлинеарны, то построим сумму A + B = = +.

Построим вектор l A =, l (A + B) = (см. рис. 15 при l > 0 и рис. 16 при l < 0). Получим, что треугольники ОAB и OCD подобны. Из подобия треугольников и определения 13 получаем, что = l A. Отсюда находим, что l (A + B) = = =+=lA + l B.

Пространство геометрических векторов. Множество V3 всех геометрических векторов пространства является векторным пространством на полем действительных чисел относительно операций сложения векторов и умножения вектора на число (см. теоремы 6 и 9 § 1).. Также векторным пространством является множество V2 (V1) всех векторов плоскости (прямой).

Множество всех геометрических векторов, коллинеарных данному вектору A образует подпространство пространства V3 всех геометрических векторов.

Умножение вектора на число

Вектор является направленным отрезком прямой, то есть представляет собой отрезок с обозначенными граничными точками, одна из которых определяет его начало, в вторая — конец.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Особенность такого действия, как умножение вектора на число заключается в том, что число является простой численной формой величины, для которого отсутствует направление, а вектор определяется в качестве направленного отрезка, обладающего численным измерением и направлением.

Подобная операция, как и вычитание, нередко используется при решении задач в математике, геометрии и физике.

В качестве примера можно рассмотреть случай из теории, при котором по дороге движутся машины в количестве двух штук. При этом скорость первого автомобиля составляет 30 км/ч, а второго — 60 км/ч. Достаточно просто определить, что вторая машина передвигается со скоростью, которая в два раза больше, чем скорость первой машины. Таким образом, скорость второго транспортного средства допустимо выразить с помощью скорости первого автомобиля путем умножения скорости первой машины на два.

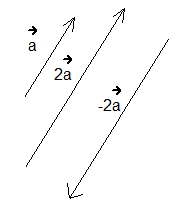
Геометрическая и алгебраическая интерпретация умножения

Геометрическая интерпретация: произведением ненулевого вектора на число является вектор, который коллинеарный заданному, то есть сонаправлен данному вектору в том случае, когда число больше нуля, либо имеет противоположное направление при отрицательном значении числа, а его модель равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация: произведение ненулевого вектора на число представляет собой вектор с координатами, равными соответствующим координатам данного вектора, умноженным на число.

Яркий пример умножения вектора на число является второй закон Ньютона, который часто применяют при решении задач в физике. Если умножить обе части закона Ньютона на массу тела, то формула примет следующий вид:

Рассматриваемая формула записана в векторном виде:

В таком случае говорят не только о модулях, то есть длинах векторов. С помощью векторного вида можно определить направление вектора. Согласно рассмотренному ранее определению произведения вектора на число, результат подобной операции не влияет на направление вектора. Его нельзя повернуть на какой-либо угол путем умножения на число. Результат произведения отличается лишь длиной вектора. Таким образом, векторы (vec) и (vec) характеризуются одинаковым направлением, но отличается по длине. В данном случае длина векторов отличается в m раз.

Понятие, основные свойства

В том случае, когда вектор (vec) равен произведению ненулевого числа k и ненулевого вектора (vec) , то есть (vec=k*vec) , справедливы следующие утверждения:

Вектор можно умножить на число в виде скалярной величины. При этом в результате получится тоже вектор. После операции умножения длина заданного вектора изменится:

• длина вектора будет увеличена при умножении на число, модуль которого больше 1;
• длина вектора уменьшится в том случае, когда модуль числа меньше 1.

Если вектор умножить на положительное число, полученный вектор будет обладать таким же направлением, что и первоначальный. В том случае, когда предполагается произведение вектора на отрицательное число, полученный в результате вектор будет направлен в противоположную сторону.

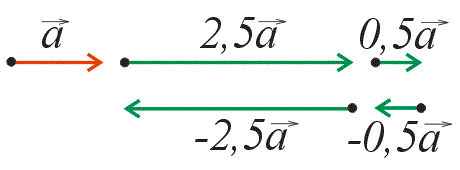
При произведении вектора на число, он не может быть повернут на какой-либо угол по отношению к исходному положению. Таким образом, заданный и полученный векторы параллельны друг другу.

В том случае, когда есть информация о координатах вектора, при умножении его на число следует умножить каждую координату рассматриваемого вектора на данное число.

Данная запись представляет собой координаты вектора (vec.)

Формулы применяющиеся при перемножении вектора и числа

В случае умножения вектора на число удобно использовать формулу умножения, предназначенную для решения плоских задач. При этом произведение вектора (vec=left;a_ right>) и какого-то числа k вычисляют по формуле:

Примеры задач с решением

В данном случае целесообразно воспользоваться формулой для решения плоских задач:

В случае пространственной задачи следует воспользоваться следующей формулой:

Подставив числовые значения, получим:

Исходя из определения, для умножения заданного вектора на число (lambda =2) требуется каждую координату вектора (bar) умножить на это число. Таким образом:

В том случае, когда требуется найти искомое произведение, следует умножить каждую координату заданного вектора (bar) на число (lambda =-3) . В результате умножения вектора на число получим:

Согласно анализу рассмотренных закономерностей, действия с векторами аналогичны действиям с алгебраическими выражениями. По этому принципу требуется упростить следующую запись:

В первую очередь следует раскрыть скобки:

Далее необходимо привести подобные:

Имеется некий отрезок АВ. Точка С является серединой данного отрезка, точка О представляет собой произвольную точку плоскости. Также (vec=vec) и (vec=vec.) Требуется доказать, что:

Используя правило треугольника, можно выразить вектор (vec) в виде суммы двух векторов:

Кроме того, следует отметить, что:

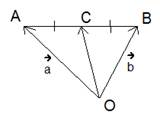
В результате получилась система двух уравнений:

Далее необходимо сложить уравнения системы:

Исходя из того, что С является серединой АВ, следует вывод: модули данных векторов равны, но они обладают разными направлениями. Таким образом, сумма векторов является нулевым вектором. В результате:

При делении обеих частей уравнения на 2 получим:

Следует раскрыть скобки и привести подобные:

Требуется доказать, что средняя линия трапеции и ее основания параллельны друг другу, а также средняя линия трапеции равна половине суммы оснований.

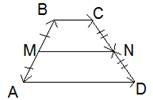
Известно, что средней линией трапеции соединены ее боковые стороны. Основания трапеции параллельны друг другу. Согласно правилу многоугольника, можно выразить вектор vec как сумму векторов:

С другой стороны:

В результате получена система уравнений:

Следует сложить уравнения системы:

Векторы (vec) и (vec) обладают противоположными направлениями и в сумме дают нулевой вектор, так как М — середина АВ, то есть модули данных векторов равны, кроме того, они противонаправлены. Аналогично векторы (vec) и (vec) дают в сумме нулевой вектор. Таким образом, получаем:

Затем можно поделить обе части уравнения на 2:

В результате получено доказательство того, что средняя линия равна половине суммы оснований. Кроме того, прямая MN параллельна основаниям трапеции.

Векторы на ЕГЭ по математике. Действия над векторами

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с 2 . Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:

Здесь в скобках записаны координаты вектора – по x и по y .
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

Сложение векторов

Для сложения векторов есть два способа.

1 . Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .

При сложении векторов и получаем:

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и – это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

Из формулы для скалярного произведения можно найти угол между векторами:

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.