Признаки выпуклости четырехугольника, его свойства и рисунки, почему выпуклый, диагонали выпуклого четырехугольника,свойство диагоналей,неправильный четырёхугольник,выпуклые 4

Что такое выпуклый четырехугольник и как определить сумму его углов

Если на плоскости имеются четыре точки, из которых никакие три не принадлежит одной прямой, то их можно попарно соединить отрезками. В результате получится фигура с четырьмя углами, содержащая две диагонали, при пересечении которых получится выпуклый четырехугольник.

Существует несколько видов фигур с четырьмя углами, но не все они являются выпуклыми. Слева рисунок отображает выпуклый четырехугольник, все его внутренние точки находятся в одной полуплоскости относительно прямой l, на которой лежит сторона AD. Для среднего данное условие выполняется, но его нельзя считать выпуклым, потому что его стороны пересекаются. Такие четырехугольники называются самопересекающимися. Правый тоже не является выпуклым, так как две его точки B и C лежат в разных полуплоскостях относительно разбиения прямой l.

На основании вышесказанного дадим определение. Выпуклым четырехугольником называется фигура, состоящая из четырех точек и четырех отрезков, которые последовательно их соединяют. Главное условие: никакие три точки не должны одновременно лежать на одной прямой, а соединяющие отрезки пересекаться.

Виды выпуклых четырехугольников:

• прямоугольник,
• параллелограмм,
• трапеция,
• ромб,
• квадрат.

Перечисленные отношения между множествами фигур упрощают доказательства теорем (предложений, выражающих свойства). Например, если теорема доказана для параллелограмма (будет ли параллелограмм выпуклым? и т.д.), то она будет верна и для любого соответствующего подмножества фигур. Если же доказана более общая теорема для выпуклого четырехугольника, то она будет верна и для параллелограмма, и для трапеции.

Свойства

• сумма углов 360 градусов,
• диагонали могут пересекаться в одной точке.

Если сумма углов равна 360, это следствие более общего случая – четырехугольника, не имеющего пересекающихся отрезков. Но для выпуклого обычно проводят отдельное и очень простое доказательство. Если внутри выпуклого четырехугольника провести диагональ, то она разобьет его на два треугольника. Как известно, сумма углов в треугольнике равна 180. Сложив все получившиеся углы, получаем величину 360.

Если взять средние точки всех сторон произвольного выпуклого четырехугольника и построить на них новый, то он окажется параллелограммом (Теорема Вариньона).

Доказательство на следующем фото. Выпуклый четырёхугольник ABCD имеет на каждой из сторон точку, делящую эту сторону пополам. Рассмотрим отрезок FG. Это средняя линия треугольника DAB, параллельная диагонали DB. Это следует из подобия треугольников DAB и FAG.

Аналогично проводятся рассуждения для треугольников DBC и EHC. Из чего следует параллельность DB и EH. Поскольку отрезки FG и EH параллельны диагонали DB, то и сами параллельны.

Аналогично доказывается, что отрезки FE и GH параллельны. Так как противолежащие стороны EFGH попарно параллельны, значит, это параллелограмм.

Обратите внимание! Теорема Вариньона справедлива для всех четырехугольников, невыпуклых и самопересекающихся. Если взять середины диагоналей, то можно построить еще два параллелограмма. Центры всех трех параллелограммов окажутся на одной прямой.

Если выпуклый четырёхугольник имеет свойство взаимной перпендикулярности своих диагоналей, то суммы квадратов его противоположных сторон у него равны. Это доказывается при помощи теоремы Пифагора, как показано на следующем чертеже:

Квадрат каждой из сторон выражается через сумму квадратов отрезков диагоналей, ограниченных вершинами и точкой пересечения. Для удобства мы обозначаем их малыми буквами латинского алфавита, совпадающими с названием вершин. Затем выписываем выражения для сумм квадратов противолежащих сторон:

В правой части каждого из выражений стоит одна и та же сумма слагаемых. Следовательно, равны и правые части между собой, что доказывает теорема.

Вписанные и описанные

Часто требуется проверить, не лежат ли вершины четырехугольника на окружности, или существует ли окружность, вписанная в 4-угольник. Центр описанной окружности находится в точке пересечения срединных перпендикуляров к сторонам, а центр вписанной – на пересечении биссектрис внутренних углов.

Если сумма противоположных углов составляет 180, то рядом с ними можно описать окружность, другими словами, существует окружность, на которой лежат все вершины четырехугольника. Его называют вписанным (подразумевается, что в окружность). Верно и обратное утверждение, то есть выраженное в теореме условие необходимое и достаточное.

Расчет площади

Площадь, которую имеет любой выпуклый четырёхугольник, равна половине произведения длин диагоналей на синус угла между ними. Докажем это правило.

Здесь опять поможет теорема Вариньона (мы имеем “большой” параллелограмм, о котором сразу не было сказано). Проведем прямые, параллельные диагоналям, через вершины A, B, C, D исходного прямоугольника. Мы получим параллелограмм EFGH. Его площадь равна сумме площадей параллелограммов AFBO, BGCO, CHDO, DEAO. Но каждый из перечисленных делится своей диагональю на пару треугольников с равными площадями. С другой стороны, в силу параллельности диагоналей ADCD сторонам внешнего параллелограмма, мы можем применить формулу площади:

Полезное видео

Подведем итоги

Фигуру, состоящую из четырех углов, можно часто увидеть в обычной жизни, такую форму обычно имеют земельные участки, здания, параллелограммы служат для построения векторных базисов на плоскости. Не случайно 4-угольники хорошо изучены и установлено большое число свойств, связанных с ними.

Понятие выпуклого четырехугольника, его свойства и признаки

Выпуклый четырехугольник — это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.

Как видно, определение довольно легко запоминающееся.

Выпуклый четырехугольник

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

1. параллелограмм;
2. квадрат;
3. прямоугольник;
4. трапеция;
5. ромб.

Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

На рисунке изображена выпуклая трапеция. Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка [AB]. Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.

Является ли параллелограмм выпуклым четырехугольником?

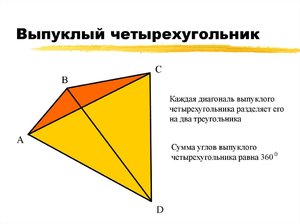
Выше показано изображение параллелограмма. Как видно из рисунка, параллелограмм также является выпуклым. Если посмотреть на фигуру относительно прямых, на которых лежат отрезки AB, BC, CD и AD, то становится понятно, что она всегда находится на одной плоскости от этих прямых. Основными же признаками параллелограмма является то, что его стороны попарно параллельны и равны так же, как и противоположные углы равны между собой.

Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.

В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам. Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Другие свойства и признаки выпуклости четырехугольника

Конкретно по этому термину очень сложно назвать какие-то определенные свойства и признаки. Легче обособить по различным видам четырехугольников такого типа. Начать можно с параллелограмма. Мы уже знаем, что это четырехугольная фигура, стороны которой попарно параллельны и равны. При этом, сюда же включается свойство диагоналей параллелограмма пересекаться между собой, а также сам по себе признак выпуклости фигуры: параллелограмм находится всегда в одной плоскости и по одну сторону относительно любой из своих сторон.

Итак, известны основные признаки и свойства:

1. сумма углов четырехугольника равна 360 градусам;
2. диагонали фигур пересекаются в одной точке.

Далее рассмотрим каждый четырехугольник по отдельности.

Прямоугольник. Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название — прямоугольник.

Квадрат, тот же параллелограмм, но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.

Трапеция — очень интересная фигура. Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.

Ромб — не менее интересная фигура. Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.

Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.

Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.

Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.

На рисунках изображены четырехугольники.

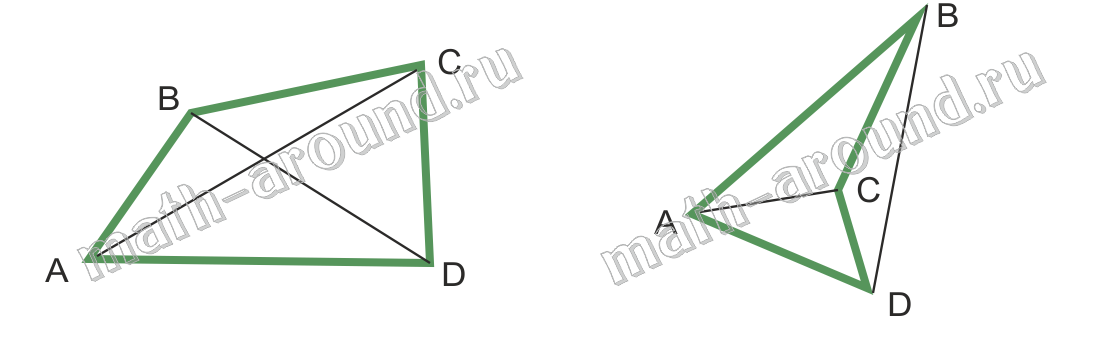
Точки А, В, С и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD – сторонами. Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.

Четырехугольники бывают выпуклые (на рисунке – левый) и невыпуклые (на рисунке – правый).

Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD – на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD – не разделяет).

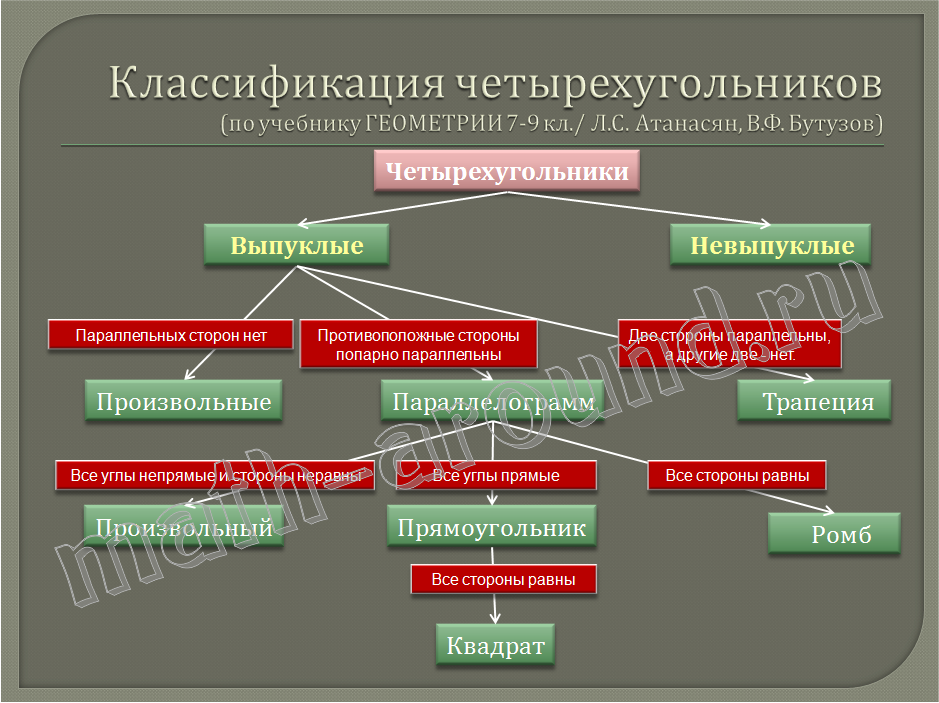
Рассмотрим основные виды четырехугольников, их свойства, формулы площади:

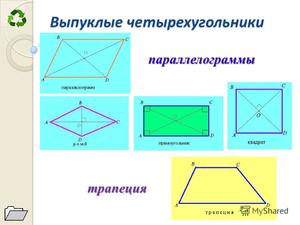
Параллелограмм

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

ABCD-параллелограмм: AB||DC, AD||BC

Свойства:

Признаки параллелограмма:

1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Площадь параллелограмма:

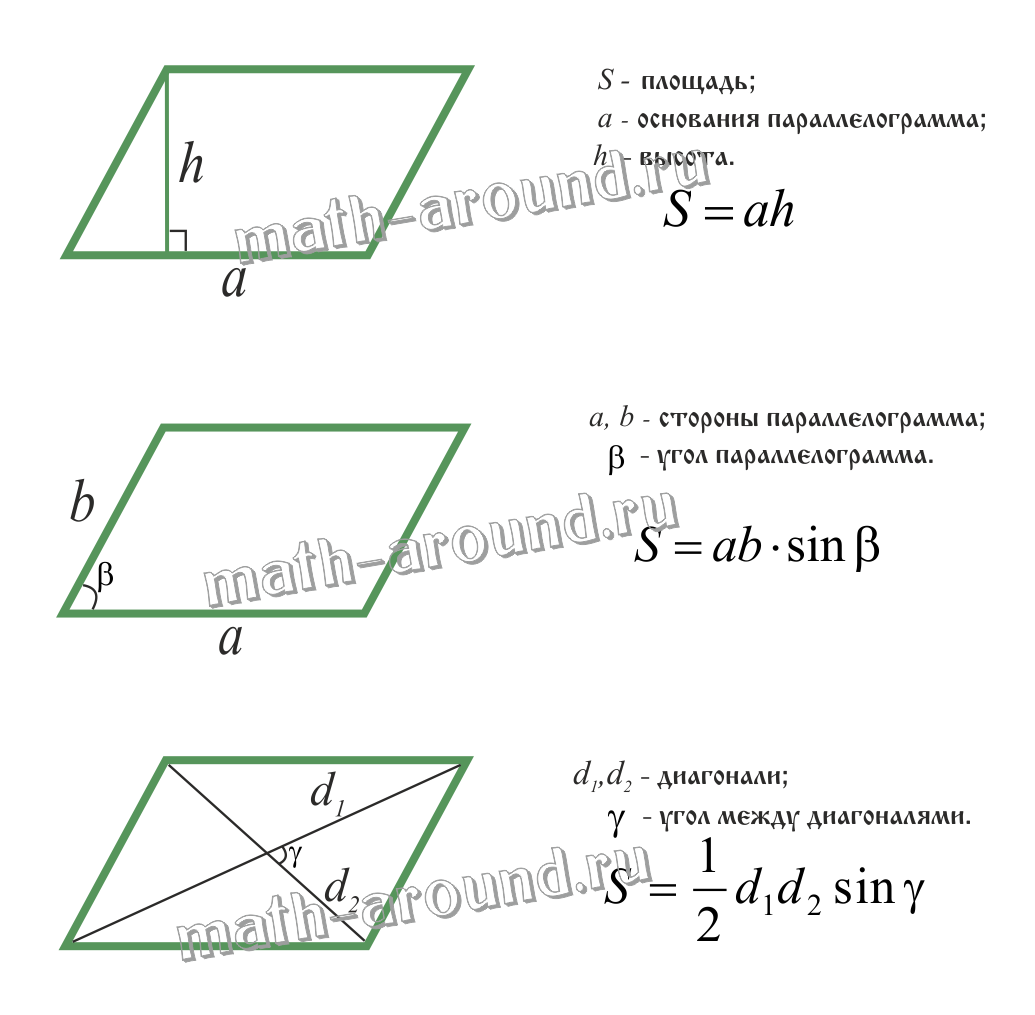
Трапеция

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основаниями называются параллельные стороны, а две другие стороны – боковыми сторонами.

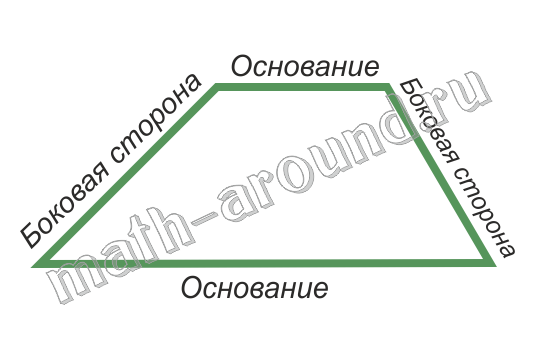
Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

ТЕОРЕМА.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

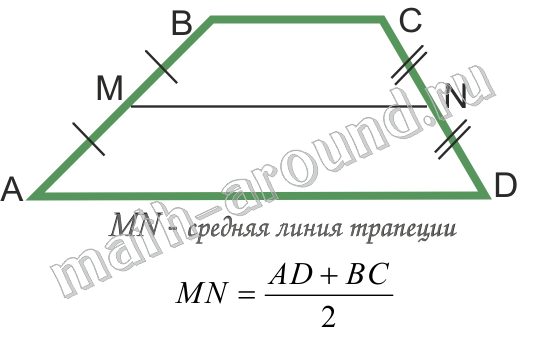
Площадь трапеции:

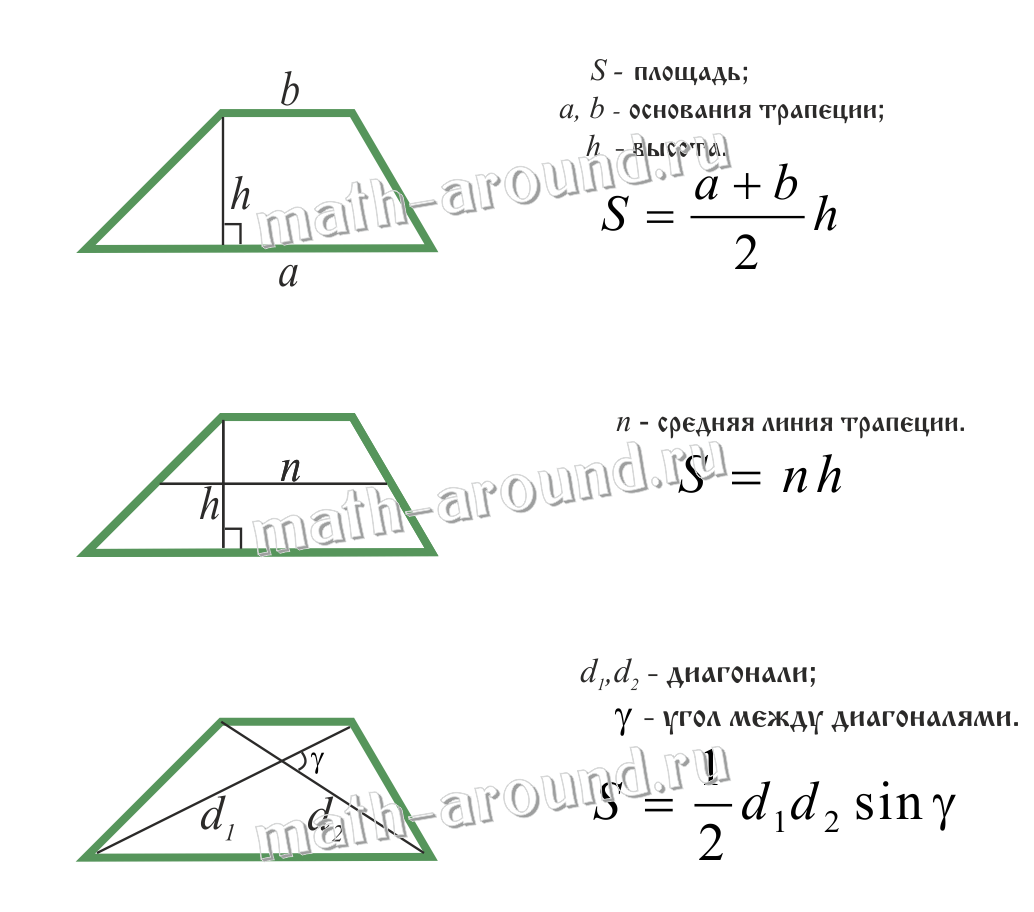
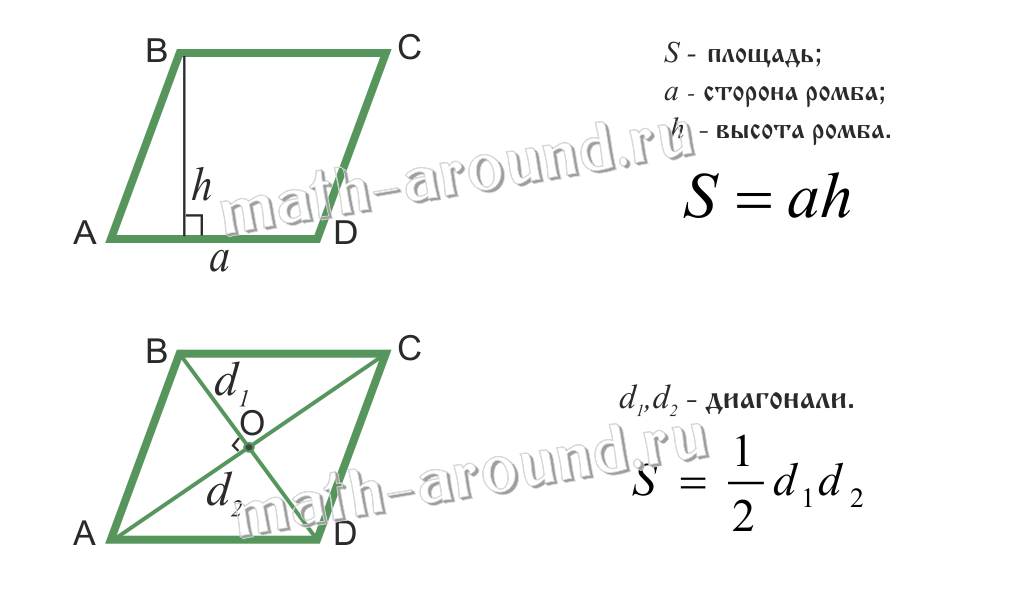
Ромбом называется параллелограмм, у которого все стороны равны.

Свойства:

Площадь ромба:

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы равны.

Свойства:

Признак прямоугольника:

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Площадь прямоугольника:

Квадрат

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства:

Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).

Площадь квадрата:

1. отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
2. оставить комментарий ниже.

Автор: Аникина Марина

Комментарии к этой заметке:

Очень понравилась эта статья ) Все интересно и понятно) Очень помогло! Спасибо)

Оглавление: Многоугольники Четырехугольник Свойства четырехугольника Свойство диагоналей выпуклого четырехугольника Характеристическое свойство фигуры. – презентация

Презентация на тему: ” Оглавление: Многоугольники Четырехугольник Свойства четырехугольника Свойство диагоналей выпуклого четырехугольника Характеристическое свойство фигуры.” — Транскрипт:

1 Оглавление: Многоугольники Четырехугольник Свойства четырехугольника Свойство диагоналей выпуклого четырехугольника Характеристическое свойство фигуры Площадь ПараллелограмПрямоугольник м Ромб Трапеция Виды трапеций Площадь Квадрат

2 Многоугольником называется геометрическая фигура, состоящая из n (n больше или равно 3) точек плоскости, не лежащих на одной прямой и попарно соединённых не пересекающимися отрезками. Многоугольник – это замкнутая ломаная линия. Существуют три различных варианта определения: Плоские замкнутые ломаные; Плоские замкнутые ломаные без самопересечений; Части плоскости, ограниченные ломаными. Вершины ломаной называются вершинами многоугольника, а отрезки сторонами многоугольника. Свойства Сумма внутренних углов плоского выпуклого n-угольника равна (в градусах) (в радианах).радианах Число диагоналей всякого многоугольника равно n(n 3) / 2, где n число сторон.

3 Четырёхугольник это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольникимногоугольниквершиныстороны Виды четырехугольников Параллелограмм Прямоугольник Ромб Квадрат Трапеция Дельтоид Выкулый не выпуклый

4 Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей. Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам. Средние линии Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин. Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

5 На рисунке 1 диагонали AC и BD выпуклого четырехугольника ABCD пересекаются в точке O, а диагонали EG и FH невыпуклого четырехугольника EFGH не пересекаются. Это свойство оналей характерно для любого выпуклого (и соответственно невыпуклого) четырехугольника. Однако при всей его очевидности строгое обоснование этого свойства оказывается достаточно сложным. Предварительно рассмотрим два вспомогательных утверждения. Напомним, что согласно одной из аксиом планиметрии каждая прямая а разделяет плоскость на две полуплоскости так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а. Прямая а называется границей каждой из этих полуплоскостей, ее точки не принадлежат ни одной из полуплоскостей. рисунок 1 рисунок 2

6 Утверждение 1. Если начало луча AB (точка A) лежит на прямой а,а точка B-в какой-то полуплоскости с границей а, то и весь луч лежит в этой полуплоскости (рисунок 3) рисунок 3

7 Свойство диагоналей выпуклого четырехугольника Рассмотрим неразвернутый угол ACB (рисунок 4). Прямая BC разделяет всю плоскость на две полуплоскости. В одной из них лежит луч CA. Обозначим эту полуплоскость буквой a. Точно так же прямая AC разделяет всю плоскость на две полуплоскости, в одной из которых лежит луч CB. Обозначим эту полуплоскость буквой p. Общая часть полуплоскостей а и p называется внутренней областью угла ACB. рисунок 4

8 Свойство диагоналей выпуклого четырехугольника Утверждение 2. Если точки А и В лежат на разных сторонах неразвернутого угла с вершиной С, а точка D лежит внутри угла АСВ (т.е. в его внутренней области), то луч СD пересекает отрезок АВ (рисунок 5) С наглядной точки зрения утверждения 1 и 2 совершенно очевидны. рисунок 5

9 Свойство диагоналей выпуклого четырехугольника Теоремы. Диагонали выпуклого четырехугольника пересекаются, а невыпуклого не пересекаются. Доказательство. 1) Рассмотрим выпуклый четырехугольник ABCD (рисунок 6). рисунок 6 2) Рассмотрим теперь невыпуклый четырехугольник ABCD(рисунок 7). рисунок 7 Следствие. Если диагонали четырехугольника пересекаются, то этот четырехугольник выпуклый

10 Х АРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО ФИГУРЫ Утверждение о характеристическом свойстве фигуры можно сформулировать с использованием словосочетания тогда и только тогда. Например: диагонали четырехугольника пересекаются тогда и только тогда, когда он является выпуклым. Площадь Площадь произвольного выпуклого четырёхугольника равна:, где d 1, d 2 диагонали и α угол между диагоналями., где e, f длины диагоналей, a, b, c, d – длины сторон., где p полупериметр. Из этой формулы для вписанных 4- угольников следует формула Брахмагупты.формула Брахмагупты Особые случаи Если 4-угольник и вписан и описан, то.

11 Площадь. Площадь произвольного выпуклого четырёхугольника равна: Площадь, где d 1, d 2 диагонали и α угол между диагоналями., где e, f длины диагоналей, a, b, c, d – длины сторон., где p полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.формула Брахмагупты Особые случаи Если 4-угольник и вписан и описан, то

12 Параллелограмм Признаки параллелограмма Четырехугольник является параллелограммом, если выполнено любое из следующих условий: противоположные стороны четырехугольника попарно равны; противоположные углы четырехугольника попарно равны; диагонали четырехугольника пересекаются и точкой пересечения делятся попалам; две стороны четырехугольника равны и параллельны.

13 Свойства Диагонали прямоугольника равны. Прямоугольник является параллелограммом его противоположные стороны параллельны. параллелограммом Стороны прямоугольника являются одновременно его высотами. Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора). теореме Пифагора Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности. Стороны и диагонали Длиной прямоугольника называют длину более длинной пары его сторон, а шириной длину более короткой пары сторон. Длина диагонали прямоугольника вычисляется по теореме Пифагора и равна квадратному корню из суммы квадратов длины и ширины.теореме Пифагора

14 Свойства Ромб является параллелограммом. Его противолежащие стороны попарно параллельны, АВ || CD, AD || ВС.параллелограммом Диагонали ромба пересекаются под прямым углом (AC BD) и в точке пересечения делятся пополам. Диагонали ромба являются биссектрисами его углов ( DCA = BCA, ABD = CBD и т. д.). биссектрисами Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.Сумма Площадь ромба Площадь ромба равна половине произведения его диагоналей. Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту. Кроме того площадь ромба может быть вычислена по формуле: где угол между двумя смежными сторонами ромба.

15 Т РАПЕЦИЯ Элементы трапеции Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.средней линией Расстояние между основаниями называется высотой трапеции.высотой

16 Прямоугольная трапеция Равнобокая трапеция Свойства Средняя линия трапеции параллельна основаниям и равна их полусумме. Отрезок, соединяющий середины диагоналей, равен полуразности оснований. (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.теорема Фалесаугла В равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции. В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой – полуразности оснований. У равнобедренной трапеции углы при любом основании равны. У равнобедренной трапеции диагонали равны. Если трапеция равнобедренная, то около неё можно описать окружность.описатьокружность Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.вписать окружность В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой. Если у равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. Если сумма углов при любом основании трапеции равна 90°, то отрезок соединяющий середины оснований равен их полуразности.

17 В случае, если a и b основания и h высота, формула площади: площади Формула, где a, b основания, c и d боковые стороны трапеции: Площадь равнобедренной трапеции с углом при основании равном 30° и радиусом вписанной окружности равном r : S = 8r 2

18 Свойства Квадрат может быть определён как прямоугольник, у которого две смежные стороны равны прямоугольник ромб, у которого все углы прямые (любой квадрат является ромбом, но не любой ромб является квадратом). ромб Пусть t сторона квадрата, R радиус описанной окружности, r радиус вписанной окружности. Тогда Радиус вписанной окружности квадрата равен:, Радиус описанной окружности квадрата равен:, периметр квадрата равен: периметр, площадь S равна площадь S = t 2 = 2R 2 = 4r 2. Квадрат обладает наибольшей симметрией среди всех четырёхугольников. Он имеет одну ось симметрии четвёртого порядка (ось, перпендикулярная плоскости квадрата и проходящая через его центр);ось симметрии четыре оси симметрии второго порядка (что для плоской фигуры эквивалентно отражениям), из которых две проходят вдоль диагоналей квадрата, а другие две параллельно сторонам.

Четырёхугольник

На этом уроке мы рассмотрим такую геометрическую фигуру, как четырехугольник. Введем понятие четырехугольника. Сформируем представления о его вершинах и сторонах. Рассмотрим, какие четырехугольники называют выпуклыми, а какие невыпуклыми. Кроме того поговорим о диагоналях и периметре четырехугольника. И выясним, что сумма углов выпуклого четырехугольника равна 360°. А также закрепим изученный материал в практической части урока.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока “Четырёхугольник”

На прошлом уроке мы с вами говорили о многоугольниках. Напомним, что многоугольником называется геометрическая фигура, которая состоит из отрезков и внутренней области. Точки A₁, A₂, A₃ и т.д., A_n-1, A_n называют вершинами многоугольника, а отрезки A₁A₂, A₂A₃,…, A_n-1A_n, A_n называют сторонами многоугольника.

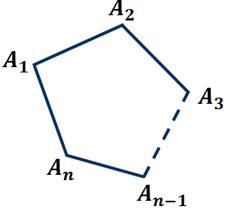
Многоугольник с n вершинами называют n-угольником.

На этом уроке мы поговорим о четырёхугольниках. Итак, четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.

При этом никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

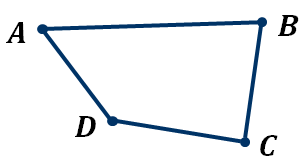
Точки A, B, C и D называются вершинами четырёхугольника. А отрезки AB, BC, CD и DA, соединяющие эти точки называются сторонами четырёхугольника.

Давайте посмотрим на следующие фигуры.

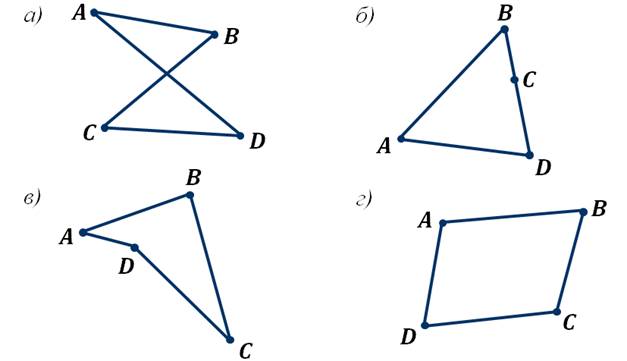
Каждая фигура состоит из четырёх точек и четырёх отрезков, которые последовательно соединяют эти точки. Но обратите внимание, что у первой фигуры отрезки AD и BC пересекаются, а, следовательно, она не является четырёхугольником. У следующей фигуры точки B, C и D лежат на одной прямой, а значит, она также не является четырёхугольником. Следующая фигура является четырёхугольником, так как у неё никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются. И последняя фигура также является четырёхугольником, так как никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

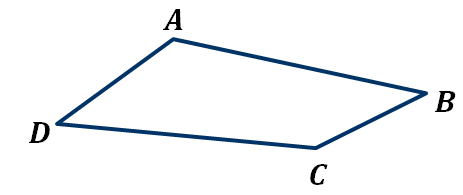
Вершины четырехугольника, принадлежащие одной стороне, называются соседними. Например, вершины A и B, А и D являются соседними.

Вершины, которые не являются соседними, называются противоположными. Так в нашем четырёхугольнике вершины А и C, B и D являются противоположными.

Стороны четырёхугольника, исходящие из одной вершины, называются соседними. Например, стороны BC и CD являются соседними.

Стороны, не имеющие общего конца, называются противоположными. Так стороны AB и CD, AD и BC являются противоположными.

Четырёхугольники бывают выпуклыми и невыпуклыми.

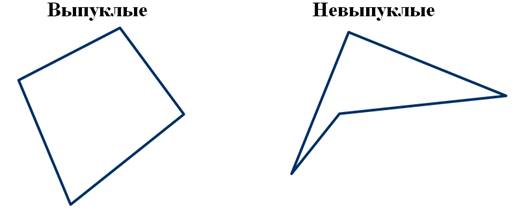
Выпуклый четырёхугольник лежит по одну сторону от прямой, проходящей через любые две соседние вершины. А вот если четырёхугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то он является невыпуклым.

Отрезки, соединяющие противоположные вершины четырёхугольника, называются диагоналями.

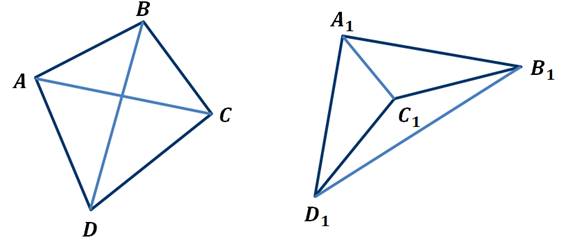
Так в выпуклом четырёхугольнике ABCD отрезки AC и BD являются диагоналями. Каждая диагональ разделяет этот четырёхугольник на два треугольника.

В невыпуклом четырёхугольнике A₁B₁C₁D₁ отрезки A₁C₁ и B₁D₁ являются диагоналями. И диагональ A₁C₁ разбивает этот четырёхугольник на два треугольника.

Периметром четырёхугольника называется сумма длин всех его сторон.

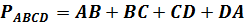
Теперь вспомнив, что сумма углов выпуклого н-угольника равна , легко можем найти сумму углов выпуклого четырёхугольника. Для этого в данное выражение вместо n подставим 4, так как четырёхугольник имеет 4 угла, выполним вычисления

и получим 360º. То есть сумма углов выпуклого четырёхугольника равна трёмстам шестидесяти градусам.

Давайте решим несколько задач.

Задача. На рисунке изображён выпуклый четырехугольник, у которого , , а . Найдите градусную меру .

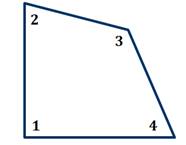
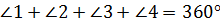
Решение. Выше мы выяснили, что сумма углов выпуклого четырёхугольника равна 360º. А тогда может составить следующее равенство: .

Теперь подставив в это равенство известные градусные меры углов, получим . Выразим угол 4: .

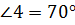
Таким образом получили, что градусная мера .

Задача. Найдите стороны четырёхугольника, если его периметр равен 66 см. Сторона больше стороны на 8 см и на столько же меньше стороны , а сторона в три раза больше стороны .

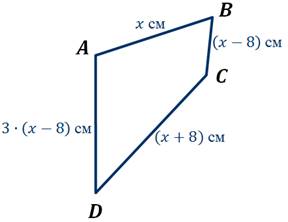
Обозначим см, тогда см,

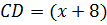
см,

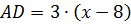
см.

.

,

,

,

,

,

.

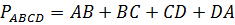
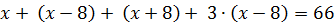
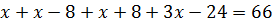
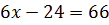
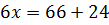
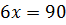
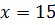
Геометрия. Урок 4. Четырехугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

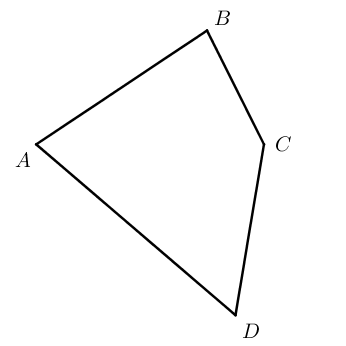
Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Параллелограмм

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

• Противолежащие стороны равны.
• Противоположные углы равны.
• Диагонали точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна 180 ° .
• Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

• Диагонали пересекаются под прямым углом.
• Диагонали являются биссектрисами углов, из которых выходят.
• Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

Как произведение стороны ромба на высоту ромба.

Как квадрат стороны ромба на синус угла между двумя сторонами.

Как полупроизведение диагоналей ромба.

Прямоугольник

Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .

Свойства прямоугольника:

• Диагонали прямоугольника равны.
• Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

• Сохраняет свойства ромба.
• Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

Как квадрат стороны.

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .

B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна 180 ° .

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.