Система отсчёта в физике и механике — что это, понятие и виды
«Физика – 10 класс»
По характеру решаемых задач механику делят на кинематику и динамику.
В кинематике описывают движение тел без выяснения причин, вызывающих данное движение
Первое, что бросается в глаза при наблюдении окружающего нас мира, — это его изменчивость. Мир не является застывшим, статичным. Изменения в нём весьма разнообразны. Но если спросить вас, какие изменения вы замечаете чаще всего, то ответ, пожалуй, будет однозначным: изменяется положение предметов (или тел, как говорят физики) относительно земли и относительно друг друга с течением времени.
Бежит ли собака, или мчится автомобиль — с ними происходит один и тот же процесс: их положение относительно земли и относительно вас изменяется с течением времени. Они перемещаются. Сжимается пружина, прогибается доска, на которую вы сели, — изменяется положение различных частей тела относительно друг друга.
Изменение положения тела или частей тела в пространстве относительно других тел с течением времени называется механическим движением.
Определение механического движения выглядит просто, но простота эта обманчива. Прочтите определение ещё раз и подумайте, все ли слова вам ясны: пространство, время, относительно других тел. Скорее всего, эти слова требуют пояснения.
Пространство и время.
Пространство и время — наиболее общие понятия физики и. наименее ясные.
Исчерпывающих сведений о пространстве и времени мы не имеем. Но и те результаты, которые получены сегодня, изложить в самом начале изучения физики невозможно.
Обычно нам вполне достаточно уметь измерять расстояние между двумя точками пространства с помощью линейки и интервалы времени с помощью часов. Линейка и часы — важнейшие приспособления для измерений в механике, да и в быту. С расстояниями и интервалами времени приходится иметь дело при изучении многих явлений во всех областях науки.
«. Относительно других тел».
Если эта часть определения механического движения ускользнула от вашего внимания, то вы рискуете не понять самого главного. Например, в купе вагона на столике лежит яблоко. Во время отправления поезда двух наблюдателей (пассажира и провожающего) просят ответить на вопрос: яблоко движется или нет?
Каждый наблюдатель оценивает положение яблока по отношению к себе. Пассажир видит, что яблоко находится на расстоянии 1 м от него и это расстояние сохраняется с течением времени. Провожающий на перроне видит, как с течением времени расстояние от него до яблока увеличивается.
Пассажир отвечает, что яблоко не совершает механического движения — оно неподвижно; провожающий говорит, что яблоко движется.
Закон относительности движения:
Характер движения тела зависит от того, относительно каких тел мы рассматриваем данное движение.
Приступим к изучению механического движения. Человечеству понадобилось около двух тысяч лет, чтобы встать на верный путь, который завершился открытием законов механического движения.
Попытки древних философов объяснить причины движения, в том числе и механического, были плодом чистой фантазии. Подобно тому, рассуждали они, как утомлённый путник ускоряет шаги по мере приближения к дому, падающий камень начинает двигаться всё быстрее и быстрее, приближаясь к матери-земле. Движения живых организмов, например кошки, казались в те времена гораздо более простыми и понятными, чем падение камня. Были, правда, и гениальные озарения. Так, греческий философ Анаксагор говорил, что Луна, если бы не двигалась, упала бы на Землю, как падает камень из пращи.
Однако подлинное развитие науки о механическом движении началось с трудов великого итальянского физика Г. Галилея.
Кинематика — это раздел механики, изучающий способы описания движений и связь между величинами, характеризующими эти движения.
Описать движение тела — это значит указать способ определения его положения в пространстве в любой момент времени.
Уже на первый взгляд задача описания кажется очень сложной. В самом деле, взгляните на клубящиеся облака, колышущиеся листья на ветке дерева. Представьте себе, какое сложное движение совершают поршни автомобиля, мчащегося по шоссе. Как же приступить к описанию движения?

Самое простое (а в физике всегда идут от простого к сложному) — это научиться описывать движение точки. Под точкой можно понимать, например, маленькую отметку, нанесённую на движущийся предмет — футбольный мяч, колесо трактора и т. д. Если мы будем знать, как происходит движение каждой такой точки (каждого очень маленького участка) тела, то мы будем знать, как движется всё тело.
Однако когда вы говорите, что пробежали на лыжах 10 км, то никто не станет уточнять, какая именно часть вашего тела преодолела расстояние в 10 км, хотя вы отнюдь не точка. В данном случае это не имеет сколько- нибудь существенного значения.
Введём понятие материальной точки — первой физической модели реальных тел.
Материальная точка — тело, размерами и формой которого можно пренебречь в условиях рассматриваемой задачи.
Система отсчёта.
Движение любого тела, как мы уже знаем, есть движение относительное. Это значит, что движение данного тела может быть различным по отношению к другим телам. Изучая движение интересующего нас тела, мы обязательно должны указать, относительно какого тела это движение рассматривается.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Чтобы рассчитать положение точки (тела) относительно выбранного тела отсчёта в зависимости от времени, надо не только связать с ним систему координат, но и суметь измерить время. Время измеряют с помощью часов. Современные часы — это сложные устройства. Они позволяют измерять время в секундах с точностью до тринадцатого знака после запятой. Естественно, ни одни механические часы такой точности обеспечить не могут. Так, одни из самых точных в стране механических часов на Спасской башне Кремля в десять тысяч раз менее точны, чем Государственный эталон времени. Если эталонные часы не корректировать, то на одну секунду они убегут или отстанут за триста тысяч лет. Понятно, что в быту нет необходимости измерять время с очень большой точностью. Но для физических исследований, космонавтики, геодезии, радиоастрономии, управления воздушным транспортом высокая точность в измерении времени просто необходима. От точности измерения времени зависит точность, с которой мы сумеем рассчитать положение тела в какой-либо момент времени.
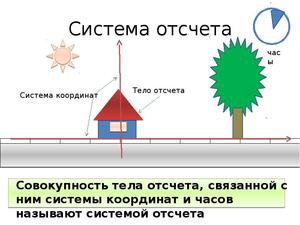
Совокупность тела отсчёта, связанной с ним системы координат и часов называют системой отсчёта.

На рисунке показана система отсчёта, выбранная для рассмотрения полёта брошенного мяча. В данном случае телом отсчёта является дом, оси координат выбраны так, что мяч летит в плоскости XOY, для определения времени берётся секундомер.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Система отсчета
Система отсчета – это совокупность тела отсчета, со связанной с ним системой координат и прибором для измерения времени.
Что такое система отсчета. Афинная и декартовая системы координат
Если рассматривать все системы отсчета относительно кинематики – они аналогичные. В кинематике не указываются преимущества одной системы отсчета при сравнении с другой. Для удобства решения выбирается наиболее приемлемая система.
Чтобы описать пространство, в котором происходит движение материальной точки, система отсчета связывается с пространственной системой координат.
Системой пространственных координат называют совокупность определений, которая может реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.
Числа, способные указать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.
Аффинная система координат – это три линейно независимых вектора (координатных осей), выходящие из одной точки, то есть из начала отсчета.
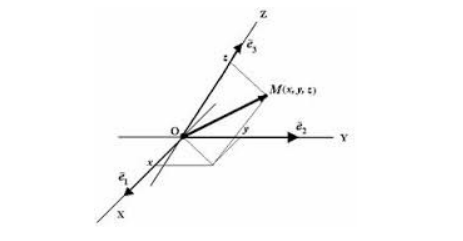
Рисунок 1 . Положение точки в афинной системе координат
Данный случай указывает на то, что определение положения материальной точки М в пространстве происходит при помощи радиус-вектора r → , проведенного через начало координат в заданную точку, движение может быть представлено в виде векторной суммы независимых перемещений вдоль трех пространственных осей выбранной системы координат.
Чаще используется декартова система координат, образованная взаимно перпендикулярными осями x , y , z . Она применима для описания прямолинейного движения и движения по незамкнутым или нецикличным кривым. Представляет из себя наглядную геометрическую интерпретацию с несложными вычислениями.
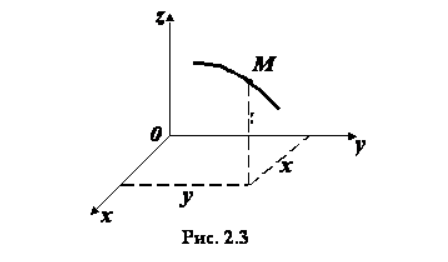
Рисунок 2 . Положение точки в декартовой системе координат
Отложенные от начала координат и вдоль осей единичные векторы называют ортами i → ; j → ; k → .
Расположение точки М находится в зависимости от значения радиус-вектора r → , соединяющего начало координат О с заданной точкой М :
r → = x i → + y j → + z k → ,
x , y , z являются декартовыми координатами точки М или проекциями радиус-вектора на соответствующие оси координат, первая производная которого дает значение мгновенной скорости точки. При известных значениях изменений во времени координат или радиус-вектора, то есть определение x = x ( t ) ; y = y ( t ) , задается характер движения тела в пространстве.
Чтобы однозначно определить положение точки М в пространстве, то предполагают наличие зависимости радиус-вектора r → от параметра t (времени) таким образом, что каждому значению параметра t соответствует одно значение функции:
r → = r → ( t ) = x ( t ) i → + y ( t ) j → + z ( t ) k → .
Данное равенство получило название кинематического уравнения движения материальной точки М в векторной форме.
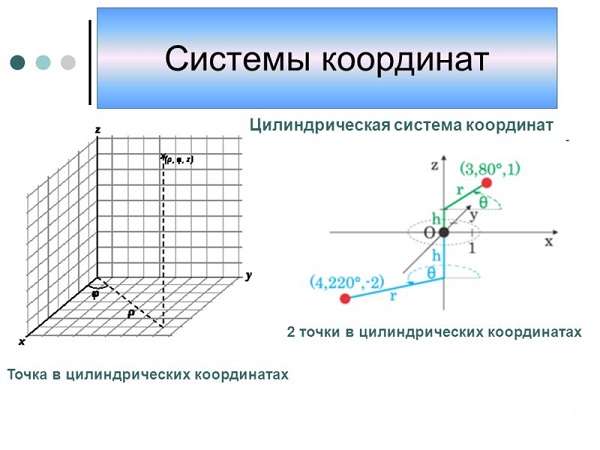
Цилиндрическая и сферическая системы координат
Чтобы описать криволинейное и аффинное движение, применяют криволинейные системы координат, которые упрощают форму записи законов движения тел для облегчения вычисления. Чаще всего используют цилиндрические и сферические системы координат.
Представление цилиндрической системы координат включает в себя трехмерную ось координат, которая является обобщением полярной на трехмерное пространство добавлением третьей координаты, задающей смещение произвольной точки М вдоль оси O Z относительно координатной плоскости O X Y .
Положение точки М может быть определено скалярами ρ , φ и z , где ρ – характеризует расстояние от точки М к оси O Z , φ – является углом, образованным проекцией радиус-вектора точки М на плоскость O X Y с положительным направлением О Х , z – проекцией точки М на ось O Z .
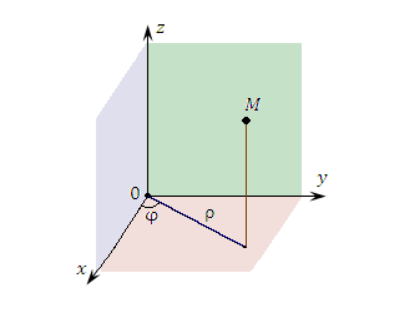
Рисунок 3 . Цилиндрические координаты точки М
Связь между декартовыми и цилиндрическими координатами может быть задана при помощи формул:
x = ρ cos φ ; y = ρ sin φ ; z = z ; ρ = x 2 + y 2 ; t g φ = y x .
Сферическая система координат характеризуется тройкой скалярных величин, которые определяют положение точки в пространстве, состоящие из длины ее радиус-вектора ρ и двух углов: φ – угла, образованного проекцией радиус-вектора точки М на плоскость O X Y с положительным направлением О Х , θ – угла, располагаемого между радиус-вектором точки М и осью O Z .
Необходимо рассмотреть сферическую систему координат O ρ θ φ , совмещенную с декартовой O x y z , причем с имеющимися пределами изменения сферических координат: 0 ≤ φ ≤ 2 π , 0 ≤ ρ ≤ ∞ .
Рисунок 4 показывает, что можно вывести формулы, связывающие сферические и декартовые координаты:
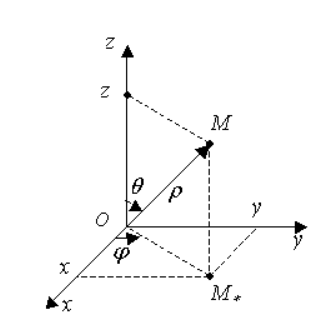
Рисунок 4 . Сферические координаты точки М
x = ρ cos φ sin θ , y = ρ sin φ sin θ , z = ρ cos θ .
Имеются другие системы криволинейных координат, с помощью которых возможно нахождение координат заданной точки: параболические, гиперболические, эллиптические и другие.
Система отсчета выбирается индивидуально относительно каждого случая в отдельности, учитывается особенность движения тела, с помощью которой определяется наиболее простой закон движения заданного тела или точки.
Система отсчёта в физике — что это, определение и виды

Определение понятия система отсчёта в физике и механике включает в себя совокупность, которая состоит из тела отсчёта, системы координат, а также времени. Именно по отношению к этим параметрам изучается движение материальной точки или же состояние её равновесия.
С точки зрения современной физики, всякое движение можно признать относительным. Таким образом, любое движение тела можно рассматривать исключительно по отношению к другому материальному объекту или же совокупности таких объектов. Например, мы не можем указать, каков характер движения Луны в общем, но может определить её перемещение относительно Солнца, Земли, Звёзд, других планет и пр.
В ряде случаев подобная закономерность бывает связана не с единой материальной точкой, а с множеством базовых точек отсчёта. Эти базовые тела отсчёта могут задавать совокупность координат.
Основные составляющие
Основными составляющими любой системы отсчёта в механике можно считать следующие компоненты:
- Тело отсчёта – это физическое тело, по отношению к которому определяется изменение положения в пространстве других тел.
- Совокупность координат, которая связывается с этим телом. В этом случае она представляет собой точку отсчёта.
- Время – это момент начала отсчитывания времени, который необходим, чтобы определить нахождение тела в пространстве в любой момент.
Для того чтобы решить конкретную задачу, необходимо определить наиболее подходящую для этого сетку координат и структуру. Идеальные часы в каждой из них потребуются лишь одни. В этом случае начало, тело отсчёта и векторы координатных осей можно выбирать произвольно.
Основные свойства

Эти структуры в физике и геометрии имеют ряд существенных различий. К физическим свойствам, которые учитываются при построении и решении задачи, относятся изотропность и однородность.
Под однородностью в физике принято понимать тождественность всех точек в пространстве. Этот фактор имеет в физике немаловажное значение. Во всех точках Земли и Солнечной системы в целом законы Ньютона в физики действуют абсолютно идентично. Благодаря этому начало отсчёта может быть размещено в любой удобной точке. И если исследователь поворачивает сетку координат вокруг начальной точки, при этом никакие другие параметры задачи не будут изменяться. Все направления, которые начинаются от этой точки, имеют абсолютно тождественные свойства. Такая закономерность называется изотропностью пространства.
Это интересно: энтропия — это что такое, где применяется термин?
Виды систем отсчёта
Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.
Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.
Инерциальные системы отсчёта
Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.
- Существование таких совокупностей подчиняется первому закону Ньютона.
- Именно в таких сетках возможно наиболее простое описание движения тел.
- По существу, инерциальная структура — это всего лишь идеальна математическая модель. Найти такую структуру в физическом мире не представляется возможным.
Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.
Неинерциальные системы отсчёта
Неинерциальные разновидности наравне с инерциальными связываются с планетой Земля. Учитывая космические масштабы, считать Землю инерциальной совокупностью можно весьма грубо и приблизительно.
Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.
Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.
Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.
Системы отсчета и их виды
В физике часто встречаются термины «система отсчета» и «инерциальная система отсчета». Ознакомимся с ними.
Что такое система отсчета
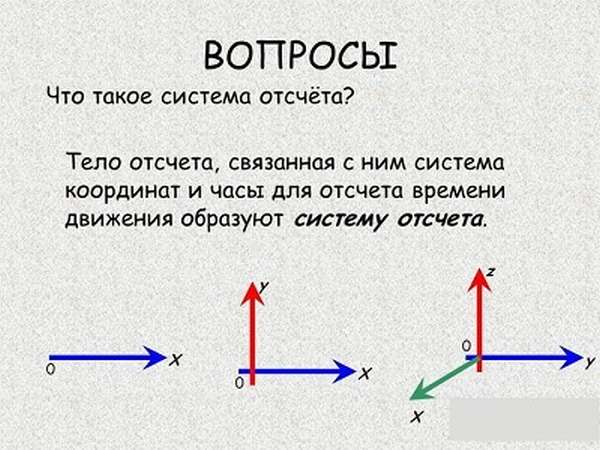
Система отсчета содержит:
- координатные оси (чтобы указывать координаты тел);
- тело отсчета (с ним связаны оси);
- часы (чтобы измерять время и считать скорость);
Если все три пункта выполнены, то говорят, что задана система отсчета.
С телом отсчета связаны координатные оси, если тело отсчета будет двигаться, то система отсчета будет передвигаться совместно с ним.
Системы отсчета используются не только в физике. В повседневной жизни мы пользуемся картами местности. При этом, на карте мы отмечаем две точки:
- точку, в которой мы находимся в данный момент – начальную точку;
- точку, в которую хотим прийти – конечную точку маршрута.
Проложив маршрут и измерив расстояние между этими точками, мы сможем посчитать расстояние, которое нужно преодолеть, чтобы переместиться. А указав интервал времени, мы сможем рассчитать, с кокой скоростью нужно двигаться, чтобы вовремя прибыть к месту назначения.
Виды систем отсчета и их сравнение
Все системы отсчета (сокращенно СО) можно разделить на два вида:
- инерциальные СО;
- не инерциальные СО;
От того, как система отсчета движется, зависит, можно ли считать ее инерциальной, или нет.
Инерциальные системы отсчета
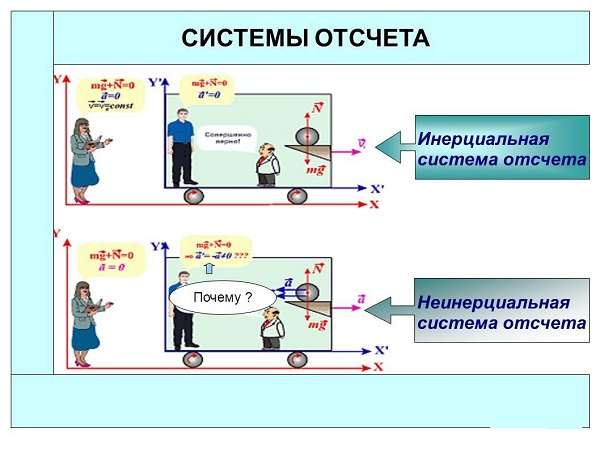
Инерциальная система отсчета — это такая, которая:
- покоится, или
- движется по прямой с одной и той же скоростью.
Другими словами, инерциальная СО не меняет вектор своей скорости ни по модулю, ни по направлению .
Примеры инерциальных систем отсчета:
- автобус находится на остановке (покоится);
- автобус едет по прямой и гладкой дороге с одной и той же скоростью;
Примечания:
1. Вместо слов «скорость не меняется», физики часто употребляют такие слова: «скорость постоянная», или «модуль вектора скорости сохраняется».
2. Скорость – это вектор, у любого вектора есть две главные характеристики:
- длина вектора (математики скажут «модуль вектора»);
- направление вектора (это направление, в котором указывает стрелка, изображающая вектор на каком-нибудь рисунке);
Подробнее о векторах и их характеристиках «здесь».
Не инерциальные системы отсчета
Не инерциальная система отсчета — это такая, которая:
- движется по прямой, но при этом ускоряется, или замедляется (меняет вектор скорости по модулю), или
- движется по кривой (меняет направление вектора скорости).
Другими словами, не инерциальная СО меняет вектор своей скорости или по модулю, или по направлению .
Бывает и так, что одновременно изменяет и по модулю, и по направлению. Главное, что изменяет. Например, гоночный автомобиль на соревнованиях входит в поворот и одновременно набирает скорость.
Примеры не инерциальных систем отсчета:
- автобус движется по прямой, но ускоряется, или замедляется;
- автобус поворачивает на перекрестке, проезжая его;
Для чего нужно знать, к какому виду отнести систему отсчета
Предположим, нам нужно решить какую-то задачу механики. Чтобы ее решить мы вводим систему отсчета. Является ли система отсчета инерциальной, нужно знать потому, что
Во всех инерциальных системах отсчета процессы механики протекают одинаково .
Для иллюстрации рассмотрим такой пример:
Представим, что мы находимся внутри пассажирского вагона. Поднимем на вытянутой руке мяч и разожмем ладонь, чтобы мяч из нее выпал. Будем изучать траекторию, по которой мяч движется. На всех рисунках пунктиром обозначено начальное положение мяча, а сплошным кругом — его конечное положение. Рассмотрим движение мяча в каждом из случаев:
Случай 1. Вагон покоится
Когда вагон покоится, свободно падающий мяч падает вертикально
Случай 2. Вагон движется равномерно прямолинейно
Красная стрелка — это вектор скорости вагона, он обозначен символом ( vec ) и указывает направление, в котором вагон движется.
Когда вагон движется равномерно прямолинейно, свободно падающий мяч падает вертикально
Случай 3. Вагон движется прямолинейно равнозамедленно
Рис.3. Вид сбоку. Вагон замедляется, двигаясь по прямой – мяч падает, отклоняясь вперед по ходу движения
Вектор скорости вагона обозначен символом ( vec ) и указывает направление, в котором вагон движется. Вектор ускорения вагона обозначен символом ( vec ). Вагон замедляется, так как скорость и ускорение направлены в противоположные стороны.
Когда вагон движется прямолинейно равнозамедленно, свободно падающий мяч отклоняется от вертикали.
Случай 4. Вагон движется прямолинейно равноускоренно
Рис.4. Вид сбоку. Вагон ускоряется, двигаясь по прямой – мяч падает, отклоняясь назад по ходу движения
Вектор скорости вагона ( vec ) и вектор ускорения вагона ( vec ) сонаправлены. Это говорит о том, что вагон ускоряется.
Когда вагон движется прямолинейно равноускоренно, свободно падающий мяч отклоняется от вертикали
Случай 5. Вагон движется криволинейно
Рис.5. Вид сверху. Вагон меняет направление движения (поворачивает) – мяч падает, отклоняясь в сторону, противоположную повороту
На рисунке представлена одна из возможных траекторий движения мяча. Траектория мяча будет зависеть от того, будет ли вагон, входящий в поворот, ускоряться, или замедляться.
Изогнутая стрелка указывает направление, в котором вагон поворачивает (изменяет направление движения).
Когда вагон движется криволинейно, свободно падающий мяч отклоняется от вертикали.
Подведем итог:
В первых двух случаях (см. рис. №1, №2), траектории мяча были одинаковыми. В этих двух случаях вагон является инерциальной системой отсчета.
Рисунки №3, №4 и №5 иллюстрируют неинерциальные системы отсчета. В случаях, представленных на этих рисунках, траектории мяча различаются. Формы траекторий зависят от дополнительных сил, действующих в неинерциальных системах отсчета на мяч.
Какие бывают системы отсчета в физике и что это такое
Для решения задач механики необходимо определить положение тела в пространстве. Только тогда можно будет рассматривать его движение. Для этого необходима система отсчета в физике и механике — это система координат и способ измерения времени.
Определение
Система отсчета в физике включает в себя тело отсчета, связанные с ним оси координат и прибор для измерения времени. Тело отсчета — это точка, от которой отсчитывают положение всех остальных точек. Она может быть выбрана в любом месте пространства. Иногда в качестве начальной точки выбирают несколько тел.
Что такое система координат? Она дает возможность однозначно определить положение точки относительно начальной точки. Каждой точке пространства сопоставляются числа (одно или несколько), которые откладываются на координатных осях.
Пример — шахматная доска. Каждая клетка обозначается буквой и цифрой, по одной оси идут буквы, по другой цифры. Благодаря им мы можем однозначно описать положение фигуры.
Важно! Оси обозначаются латинскими или греческими буквами. Они имеют положительное и отрицательное направление.
Наиболее распространенные в физике виды координат — это:
- прямоугольные, или декартовы — угол между осями прямой, используются две (на плоскости) или три (в трехмерном пространстве) оси,
- полярные — на плоскости, где в качестве координат используется расстояние от центра r и угол относительно полярной оси (полярный угол),
- цилиндрические — расширение полярных на трехмерное пространство, добавляется ось z, перпендикулярная r и плоскости, в которой лежит полярный угол,
- сферические — трехмерные, используются два угла и расстояние от центра, так построены географические и астрономические координаты.
Это интересно! Как правильно перевести МПА атмосферы
Существует множество других вариантов координат. Можно переходить из одних в другие, преобразуя координаты с помощью уравнений.
Понятие системы отсчета (СО) включает прибор для измерения времени, другими словами, часы. Он необходим, чтобы рассматривать движение точки — изменение ее положения со временем.
Изменения положения точки относительно выбранной СО описываются уравнениями движения. Они показывают, как изменяется положение точки с течением времени.
Виды систем отсчета
В зависимости от того, какие задачи надо решить, можно выбрать те или иные системы отсчета.
Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях
Инерциальная и неинерциальная
СО бывают инерциальные и неинерциальные. Понятие инерциальной СО важно для кинематики — раздела физики, изучающего движение тел.
Инерциальная СО движется прямолинейно с неизменной скоростью относительно окружающих тел. Окружающие предметы на нее не воздействуют. Если она стоит на месте — это тоже частный случай равномерного прямолинейного движения. Такие СО имеют следующие свойства:
- инерциальная СО, которая движется относительно другой инерциальной СО, также будет инерциальной,
- все законы физики выполняются в разных ИСО одинаково и имеют одинаковую форму записи,
- координаты и время в разных ИСО в классической механике связаны преобразованиями Галилея,
- в специальной теории относительности вместо них пользуются преобразованиями Лоренца, а скорость не может превышать некоторую постоянную (скорость света с).
Пример инерциальной СО — гелиоцентрическая, с центром в Солнце. СО, связанная с землей, инерциальной не будет. Наша планета движется вокруг солнца криволинейно, кроме того, на нее действует гравитация Солнца. Однако для многих задач этим ускорением и воздействием Солнца можно пренебречь. Это задачи, где «место действия» поверхность Земли. Например, если нам нужно найти скорость снаряда, выпущенного из пушки, влияние Солнца и вращение Земли нас не интересует.
Неинерциальная СО подвергается воздействию других предметов, поэтому движется с ускорением. К неинерциальным относятся и вращающиеся СО. В неинерциальных СО законы Ньютона не выполняются, но можно описывать перемещение теми же уравнениями, что и в ИСО, если ввести дополнительные силы.
Система центра масс и лабораторная
В механике также используется система центра масс (центра инерции), сокращенно с.ц.м. или с.ц.и. В качестве начала координат в такой СО выбирают центр масс нескольких объектов. Сумма их импульсов в такой СО равна нулю.
Применяют с.ц.и. чаще всего в задачах рассеяния. Задачи такого типа решают в механике и ядерной физике, например, это задачи о столкновении частиц в ускорителях.
В таких задачах также используют лабораторную СО. Она противоположна с.ц.и. В ЛСО положение частиц определяют относительно покоящейся мишени, на которой рассеиваются другие частицы.
Это интересно! Формула закона полного отражения и преломления света
Полезное видео: инерциальные и неинерциальные системы отсчёта
Относительность движения
По современным представлениям, абсолютной СО не существует. Это значит, что рассматривать движение тел можно только по отношению к другим телам. Не имеет смысла говорить о том, что предмет «двигается вообще». Причина этого — свойства пространства и времени:
- пространство изотропно, то есть в нем все направления равноценны,
- пространство однородно — все точки обладают одинаковыми свойствами,
- время однородно — нет каких-то особых моментов времени, все они равноценны.
Важно! Во времена Ньютона считалось, что можно рассматривать движение относительно абсолютного пространства, позже — относительно эфира в электродинамике Максвелла. Разработанная Эйнштейном теория относительности доказала, что абсолютного начала отсчета быть не может.
Полезное видео: определение координат тела
Вывод
Системы отсчета в физике необходимы, чтобы рассматривать движение тел. Их можно выбирать по-разному, как удобнее для конкретной задачи, так как движение относительно. Для механики важны инерциальные СО — те, которые движутся равномерно и прямолинейно относительно других тел.
Относительность движения и система отсчета в физике
Относительность движения проявляется в том, что поведение любого движущегося тела может быть определено только по отношению к какому-то другому телу, которое называют телом отсчета.
Тело отсчета и система координат
Тело отсчета выбирают произвольно. Следует отметить, что движущееся тело и тело отсчета равноправны. Каждое из них при расчете движения в случае необходимости можно рассматривать или как тело отсчета, или как тело движущееся. Например, человек стоит на Земле и наблюдает, как по дороге едет автомобиль. Человек неподвижен относительно Земли и считает Землю телом отсчета, самолет и автомобиль в этом случае тела движущиеся. Однако, пассажир автомобиля, который говорит, что дорога убегает из-под колес, тоже прав. Он считает телом отсчета автомобиль (он неподвижен относительно автомобиля), Земля при этом – тело движущееся.
Чтобы фиксировать изменение положение тела в пространстве, с телом отсчета нужно связать систему координат. Система координат – это способ задания положения объекта в пространстве.
При решении физических задач наиболее распространенной является декартова прямоугольная система координат с тремя взаимно перпендикулярными прямолинейными осями – абсциссой ( ), ординатой ( ) и аппликатой ( ). Масштабной единицей измерения длины в СИ является метр.
При ориентировании на местности пользуются полярной системой координат. По карте определяют расстояние до нужного населенного пункта. Направление движения определяют по азимуту, т.е. углу, который составляет нулевое направление с линией, соединяющей человека с нужным пунктом. Таким образом, в полярной системе координат координатами являются расстояние и угол .
В географии, астрономии и при расчетах движений спутников и космических кораблей положение всех тел определяется относительно центра Земли в сферической системе координат. Для определения положения точки в пространстве в сферической системе координат задают расстояние до начала отсчета и углы и — углы, которые составляет радиус-вектор с плоскостью нулевого гринвичского меридиана (долгота) и плоскостью экватора (широта).
Система отсчета
Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.
При решении любой задачи о движении прежде всего должна быть указана та система отсчета, в которой будет рассматриваться движение.
При рассмотрении движения относительно подвижной системы отсчета справедлив классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной:
Примеры решения задач по теме «Относительность движения»
| Задание | Самолет движется относительно воздуха со скоростью 50 м/с. Скорость ветра относительно земли 15 м/с. Какова скорость самолета относительно земли, если он движется по ветру? против ветра? перпендикулярно направлению ветра? |
| Решение | В данном случае скорость — скорость самолета относительно земли (неподвижной системы отсчета), относительная скорость самолета — это скорость самолета относительно воздуха (подвижной системы отсчета), скорость подвижной системы отсчета относительно неподвижной — это скорость ветра относительно земли. |
Направим ось по направлению ветра.
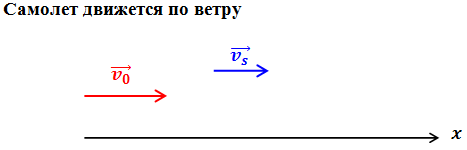
Запишем закон сложения скоростей в векторном виде:
В проекции на ось это равенство перепишется в виде:
Подставив в формулу численные значения, вычислим скорость самолета относительно земли:
(м/с)
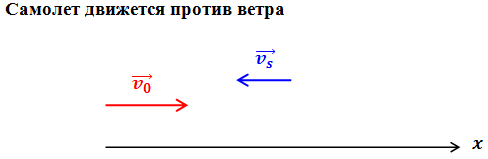
Запишем закон сложения скоростей в векторном виде:
В проекции на ось это равенство перепишется в виде:
Подставив в формулу численные значения, вычислим скорость самолета относительно земли:
(м/с)
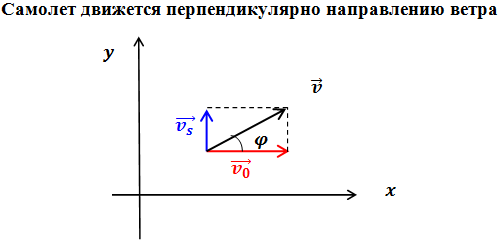
В данном случае пользуемся системой координат , направив координатные оси, как показано на рисунке.
Складываем вектора и по правилу сложения векторов. Скорость самолета относительно земли:
(м/с)
Эта величина представляет собой модуль вектора скорости. Для определения направления скорости самолета вычислим:
![]()
Таким образом, относительно земли самолет будет двигаться со скоростью 52,2 м/с под углом к горизонтальному направлению OX.





