Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света

Согласно законам геометрической оптики свет распространяется по прямой, поэтому непрозрачные предметы на экране дают тень, контуры которой повторяют контуры предмета, а свет, прошедший сквозь отверстие в шторке, образует на стене световое пятно, имеющее его форму. Однако, если присмотреться внимательнее, можно заметить, что контуры тени немного размыты — свет частично заходит за границы препятствия, отклоняясь от прямолинейного пути.

Совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, в которых проявляются отклонения от законов геометрической оптики, называются дифракцией света.

Объяснить эти явления возможно лишь с точки зрения волновой природы света. Дифракционные эффекты проявляются, когда размер непрозрачных препятствий намного превышает длину световой волны.

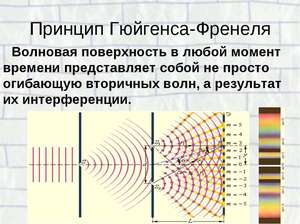
ПРИНЦИП ГЮЙГЕНСА – ФРЕНЕЛЯ

В 1678 г. голландский физик Христиан Гюйгенс сформулировал принцип, позволяющий оценивать перемещение волнового фронта световых колебаний.

Каждую точку волнового фронта можно рассматривать как источник вторичных волн, распространяющихся в сторону движения фронта волны.

Допустим, что в некоторый момент времени волновой фронт имел форму, как на рис. 16.8, а. Согласно принципу Гюйгенса каждую точку этой волновой поверхности можно рассматривать как источник вторичных сферических волн, распространяющихся вперед. За время At все вторичные волны пройдут расстояние А/ = vAt, где v — скорость света в данной среде. Огибающая этих волн (пунктир) и определяет форму и положение фронта волны через время At.

Принцип Гюйгенса объяснял, почему свет огибает препятствия. Когда он проходит, например, через отверстие в непрозрачном экране (рис. 16.8, б), то первоначально плоский фронт световой волны искривляется и свет попадает в область геометрической тени (дифракция).

Основываясь на своем принципе, Гюйгенс объяснил также законы отражения и преломления света на границе двух сред. Но этот принцип не объяснял ни прямолинейности распространения света, ни сложных интерференционных картин, образующихся на экране в результате дифракции.

Почти полтора века потребовалось, чтобы уточнить принцип Гюйгенса. Это сделал в 1816 г. французский физик Огюстен Френель. К формулировке принципа Гюйгенса он добавил всего лишь, что вторичные волны когерентны и, следовательно, должны интерферировать. Эта поправка позволила оценивать не только форму, но и интенсивность световой волны в любой точке интерференционного поля.

Чтобы оценить интенсивность света от источника S в некоторой точке М, Френель предложил делить (мысленно) волновой фронт на зоны (рис. 16.9). Их ширина выбирается так, чтобы расстояния от соседних зон до точки М отличались на половину длины световой волны. Интенсивность света в точке М будет, очевидно, равна сумме интенсивностей от всех зон волнового фронта. Так как оптическая длина хода от двух соседних зон отличается на полволны, то эти волны будут приходить в точку М в противофазе и, следовательно, гасить друг друга, поэтому амплитуду результирующего колебания можно выразить так:

где А0 — амплитуда колебаний от нулевой (центральной) зоны; >4/ — амплитуды колебаний от всех последующих зон.

Несложный расчет показывает, что все зоны Френеля имеют одну и ту же площадь и, следовательно, от них исходит один и тот же световой поток. Поэтому все разности в скобках будут (почти) равны нулю. Не скомпенсированным останется лишь свечение нулевой зоны, лежащей на прямой SM. Это и создает иллюзию, что свет от источника S до точки М идет по прямой. Так как каждая последующая зона видна из точки М под все более убывающим углом, то в действительности А >А₂ >А₃ > . и т.д. Более аккуратный расчет дает амплитуду световых колебаний в точке М, равной Ам — Ао/2.

Если нулевую зону (или несколько центральных зон) закрыть непрозрачным диском, то точка М будет освещаться первой (ближайшей к краю диска) зоной и окажется освещенной. Этот пара-

доке, получивший название пятна Пуассона, стал убедительным доказательством правильности разработанной Френелем теории дифракции света.

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

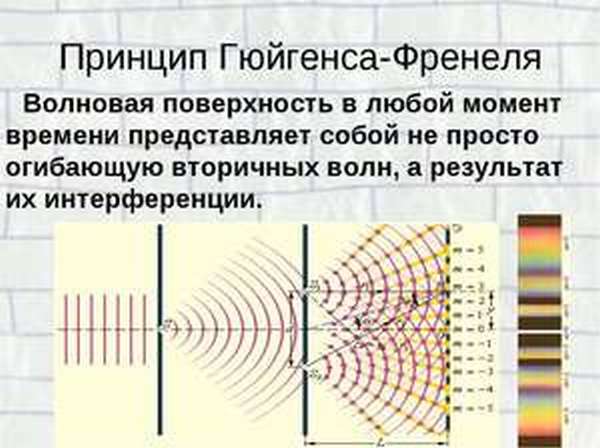
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Рисунок 3 . 8 . 1 Принцип Гюйгенса-Френеля. ∆ S 1 и ∆ S 2 – элементы волнового фронта, n 1 → и n 2 → – заданные нормали.

Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

Для определения колебания в заданной точке P , которое вызвано волной, используя принцип Френеля, находят колебания, которые вызваны в этой точке с помощью отдельных вторичных волн, которые приходят от элементов поверхности S ( ∆ S 1 , ∆ S 2 и так далее). Далее следует произвести сложение колебаний, учитывая амплитуды и фазы. Элементы, загороженные препятствиями, не учитываются при решении.

Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

Рисунок 3 . 8 . 2 Дифракция плоской волны на экране, содержащем круглое отверстие.

Р – точка наблюдения, находящаяся на оси симметрии, располагаемого на L расстоянии относительно экрана. По принципу Гюйгенса-Френеля распределить на волновой поверхности вторичные источники, совпадающие с плоскостью отверстия, где волны достигают точки Р . Интерференция волн в этой точке является причиной возникновения результирующего колебания, квадрат амплитуды которого определяется при наличии значений длин волн λ , амплитуды A 0 падающей волны и расположением элементов.

Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Иначе говоря, r 1 = L + λ 2 , r 2 = L + 2 λ 2 , r 3 = L + 3 λ 2 . . .

При рассмотрении волновой поверхности исходя из точки Р , тогда получим, что границы зон Френеля будут иметь вид концентрических окружностей. Наглядно это изображено на рисунке.

Рисунок 3 . 8 . 3 Границы зон Френеля в плоскости отверстия.

По рисунку 3 . 8 . 2 определяем радиусы ρ m зон по формуле: ρ m = ρ m 2 – L 2 = m λ L + m 2 λ 2 4 ≈ m λ L .

Зоны Френеля. Интерференционный максимум

Значение m может быть любым числом. От него зависит результат интерференции вторичных волн, проходящих точку Р . Такие открытые зоны Френеля обладают одинаковым значением площади:

S m = π ρ m 2 – π ρ m – 2 1 = π λ L = S 1 .

По теории равные площади возбуждают колебания с одинаковой амплитудой в точке наблюдения. Но каждая последующая зона угла α , располагаемая между лучом, проводимым к точке наблюдения, и нормалью относительно волновой поверхности, возрастает. Предположения Френеля говорит о том, что при увеличении угла α происходит незначительное уменьшение колебаний, то есть:

A 1 > A 2 > A 3 > . . . > A 1 , где A m обозначает амплитуду колебаний, которые были вызваны при помощи m -ой зоны.

Используя приближение, видно, что амплитуда колебаний, которая вызвана определенной зоной, равняется среднему арифметическому соседних зон. Иначе это запишем как A m = A m – 1 + A m + 1 2 .

Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

A = A 1 – A 2 + A 3 – A 4 + . . . = A 1 – ( A 2 – A 3 ) – ( A 4 – A 5 ) – . . . < A 1 .

Отсюда делаем вывод, что суммарная амплитуда в точке меньше колебаний, вызванных только при помощи одной зоны Френеля. Если все имеющиеся зоны Френеля являлись открытыми, тогда к точке наблюдения двигалась волна с амплитудой A 0 , невозмущенная препятствием. Тогда запись принимает вид:

A = A 0 + A 1 2 – A 2 + A 3 2 + A 3 2 – A 4 + A 5 2 + . . . = A 1 2 .

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Когда отверстие непрозрачного экрана дает возможность только одной зоне Френеля быть открытой, тогда наблюдается возрастание амплитуды колебаний в количестве 3 раз, а интенсивности – 4 раз. При открытии двух зон действие становится равным нулю. При наличии непрозрачного экрана с несколькими нечетными открытыми зонами, очевидно, что произойдет резкое возрастание амплитуды. При открытии 1 , 3 , 5 зон получим, что A = 6 · A 0 , I = 36 · I 0 .

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

A = A m + 1 – A m + 2 + A m + 3 – . . . = A m + 1 2 + A m + 1 2 – A m + 2 – A m + 3 2 + . . .

Иначе можно записать как A = A m + 1 2 , ибо выражения в скобках будут равняться нулю.

Когда диск может закрыть небольшие зоны, тогда A m + 1 ≈ 2 A 0 и A ≈ A 0 , можно наблюдать интерференционный максимум. Иначе его называют пятном Пуассона, которое окружается дифракционными кольцами светлого и темного цвета.

Чтобы углубиться в понятие, необходимо оценить зоны Френеля. Имеется дифракционная картина на экране с расстоянием равным L = 1 м , а значение длины волны света λ = 600 н м (красный). Отсюда получим, что радиусом первой зоны является ρ 1 = L λ ≈ 0 , 77 м м .

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

m = R 2 L λ ≥ 1 или R 2 ≥ L λ .

Название данного соотношения – критерий наблюдения дифракции.

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

m = R 2 L λ > > 1 или R 2 > > L λ .

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

Выше рассмотренный случай относится к дифракции света с удаленным источником, располагаемом на препятствиях округлой формы. При расположении точечного источника света на конечном расстоянии сферически расходящаяся волна должна падать на препятствие. Данный случай усложняет задачу. Тогда построение зон Френеля необходимо выполнять на поверхности сферической формы, показанное на рисунке 3 . 8 . 4 .

Рисунок 3 . 8 . 4 Зоны Френеля на сферическом фронте волны.

При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как

ρ m = a b a + b λ .

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Формулировка принципа Гюйгенса-Френеля

Принцип Гюйгенса-Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

Описание принципа Гюйгенса

Что объясняет

В 1678 году Христиан Гюйгенс предположил, что каждая точка поверхности, куда добирается волна света, становится вторичным источником, отражающим волну. Это объясняло поведение световых волн в прозрачных средах и при контакте с зеркальными поверхностями, но не соответствовало принятой научным сообществом на тот момент корпускулярной теории света.

Основная проблема принципа

Принципа Гюйгенса недостаточно для полного объяснения такого явления, как дифракция. Интерференция в принципе Гюйгенса не учитывалась вовсе.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Работа Френеля над принципом Гюйгенса

Что он изменил и добавил

Большинство маститых учёных — и среди них Жан Био, Пьер Лаплас, Симеон Пуассон — вслед за Исааком Ньютоном считали свет потоком частиц, или корпускул. В рамках корпускулярной теории были сделаны самые значительные открытия в оптике, например, обнаруженная в 1808 году Этьеном Малюсом поляризация света при отражении.

Волновая теория света не могла объяснить поляризацию и двойное лучепреломление, в то время как у её противников имелись на этот счет хоть и громоздкие, но все же вполне приемлемые гипотезы. В 1815 году Огюстен Френель сопоставил волновую и корпускулярную теории света и, признав преимущества корпускулярной в объяснении прямолинейного распространения света, доказал, что те же явления можно объяснить и в рамках гипотезы колебаний. Через некоторое время, исследуя явления поляризации, Френель понял, что их можно объяснить, только приняв предположение о поперечном характере световых волн. Теоретические рассуждения Гюйгенса о том, как волны огибают препятствия, Френель заменил доказательством интерференции вторичных волн.

Формулировка

Дополнение Френеля к принципу Гюйгенса доказывает, что каждый элемент волнового фронта можно считать центром возбуждения вторичных сферических волн. Световое поле в каждой точке пространства будет определяться их интерференцией.

Что объясняет принцип Гюйгенса-Френеля

Независимость волны от источника

Каждая точка поверхности, куда попадает волна, становится вторичным источником волн. Эти волны, попадая в свободное пространство, при движении вперед интерферируют только друг с другом и усиливают друг друга в одинаковых фазах. При движении назад они гасятся при интерференции с первичной, прямой волной. Фазы вторичных волн отличаются от фаз первичных.

Явление дифракции

Если внимательно взглянуть на пятно света, прошедшего через узкое отверстие, можно заметить, что его граница окружена чередующимися тёмными и светлыми полосками. Возникают они за счёт дифракции на краях отверстия.

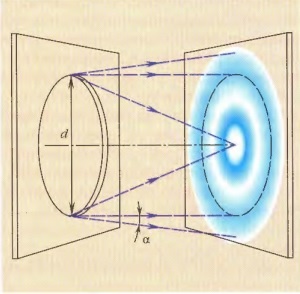
Рассмотрим сечение круглого волнового пучка, выходящего из отверстия диаметром d. Разбив пучок на множество маленьких вторичных источников, проследим, как ведут себя волны, приходящие от любого из них в разные точки пространства. Если выбрать точку наблюдения близко к оси пучка, то вторичные волны в этой точке окажутся в фазе и при сложении будут усиливать друг друга. По мере увеличения расстояния от оси разность фаз между самым близким и самым дальним источниками начнет увеличиваться, и можно обнаружить точку, где волны находятся в противофазе, гасят друг друга.

Чем дальше точка наблюдения от оси пучка, тем больше в нее приходит таких рассогласованных вторичных волн, тем слабее суммарная волна. Точный расчет показывает, что вторичные волны полностью гасят друг друга при распространении под углом к оси пучка. Следовательно, пучок из цилиндрического превращается в конический. Этот угол называют углом дифракции.

При любых условиях дифракции новая, вторичная волна отстает по фазе от первичной на (frac2) .

Несмотря на то, что абсолютно точно описать взаимодействие волн в процессе дифракции можно только в рамках векторной электромагнитной теории, скалярный принцип Гюйгенса-Френеля достаточно адекватно описывает формирование оптического изображения и применяется для решения большинства практических задач. Большая точность необходима лишь для описания работы субдлинноволновых оптических инструментов, а также оптических систем с большой числовой апертурой.

Решение уравнения по принципу

Интегральная формулировка принципа

Формулировка через интеграл по траекториям — это способ найти множество траекторий вторичных волн. Этот способ на основе принципа Гюйгенса-Френеля был адаптирован для расчета бесконечного множества траекторий квантовой амплитуды.

Сущность метода заключается в делении поверхности на столь малые части, чтобы их можно было принять за материальные точки, и последующем суммировании величин по всем участкам изменения конкретной величины. Волновой фронт, расходящийся от точечного источника, имеет вид сферы.

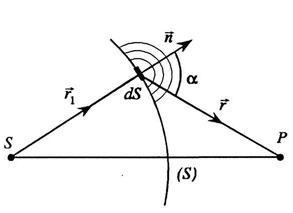
На схеме мы видим точку наблюдения Р, относительно которой определяем комплексную амплитуду поля, обусловленную действием вторичного источника на участке (ds) , по формуле:

где (f_0left(overrightarrowright)) — комплексная амплитуда поля первичной волны на участке ds;

(K(alpha)) — коэффициент наклона;

(lambda) — длина волны.

Когда в задаче идет речь о дифракции, нужно применить постулат о граничных условиях и проинтегрировать вышеприведенное выражение по поверхности S, разделяя затененные и не прикрытые экраном участки.

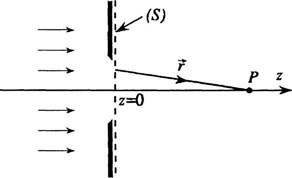
Определение комплексной амплитуды первичной волны в данном случае выглядит следующим образом:

Тогда комплексную амплитуду в точке наблюдения можно найти по формуле:

В оптических задачах часто используется метод зон Френеля. Он позволяет с помощью геометрических построений определить закономерности распределения интенсивности волн. С целью упрощения расчетов волновую поверхность делят на кольцевые зоны.

Примеры решения задач

Задача 1

Вычислить суммарную амплитуду плоской монохроматической дифрагированной волны на щели, плоскость которой перпендикулярна распространению волны, при условии, что экран расположен далеко от щели.

Решение

Так как экран далеко, можно считать, что для участка щели с координатой у расстояние до точки наблюдения равно (у;times;sinleft(psiright).)

Если мысленно разбить щель на одинаковые участки шириной (dy) , одинаковые по модулю комплексные амплитуды от соседних участков в точке наблюдения будут развернуты друг относительно друга на одинаковые углы (frac<2mathrmpi>lambda;times;dу;times;sinleft(psiright)) .

Изменение угла psi между нормалью к плоскости щели и направлением наблюдения приведет к изменению угла dvarphi между векторами комплексных амплитуд волн, пришедших от соседних участков щели.

Чтобы найти суммарную амплитуду, нужно сложить комплексные числа с одинаковыми амплитудами и разными фазами (frac<2mathrmpi>lambda;times;у;times;sinleft(psiright).)

Ответ: суммарную амплитуду можно вычислить по формуле:

(E’ = int_^ E_times exp [itimesfrac<2pi y>timessinpsi]times dy)

Задача 2

Квадратное отверстие со стороной 0,2 см освещено параллельным пучком нормально падающих лучей света.

Найти размер изображения отверстия на экране, параллельном отверстию и удаленном от него на 50 метров. За границу изображения на экране принять положение дифракционного максимума первого порядка для наиболее отклоняемых лучей (видимый спектр от 400 до 700 нм).

Решение

Напряженность электрического поля волны в данных условиях можно вычислить с помощью формулы:

Введем углы дифракции (vartheta_1) и (vartheta_2) :

Так как расстояние l достаточно велико, углы дифракции малы, соответственно, есть основания предполагать, что их тангенс примерно равен синусу. Тогда формула напряженности поля с подставленными значениями будет выглядеть так:

Интегрировав выражение, получим:

Угловое выражение дифракционных максимумов первого порядка:

Вычислим линейное расстояние D между оптической осью системы и дифракционным максимумом:

Описание и применение принципа Гюйгенса — Френеля

С давних времён люди заметили отклонение световых лучей при нахождении какого-то препятствия перед ними. Можно обратить внимание на то, как сильно искажается свет при попадании в воду: луч «ломается» из-за так называемого эффекта дифракции света. Дифракцией света называется огибание или искажение света из-за различных факторов вблизи.

Принцип Гюйгенса
Принцип Гюйгенса — Френеля
Метод зон Френеля

Принцип Гюйгенса

Работу подобного явления описал Христиан Гюйгенс. После определённого количества проведённых экспериментов со световыми волнами на водной поверхности, он предложил науке новое объяснение такого феномена и дал ему название волновой фронт. Таким образом, Христиан дал возможность понять, как будет вести себя луч света при попадании на какую-то поверхность другого типа.

Его принцип звучит следующим образом:

Точки поверхности, заметные в определённый момент времени, могут быть причиной для вторичных элементов. Площадь, которая прикасается ко всем вторичным волнам, считается волновой сферой в последующие отрезки времени.

Он объяснил, что все элементы следует рассматривать как начало сферических волн, которые имеют название как вторичные волны. Христиан заметил, что волновой фронт по своей сути является совокупностью этих точек касания, отсюда и выплывает весь его принцип. Кроме этого, вторичные элементы представляются сферической формы.

Стоит запомнить, что волновой фронт — это точки геометрического смысла, до которых доходят колебания к определённому моменту времени.

Вторичные элементы Гюйгенса представляются не как настоящие волны, а лишь дополнительные, имеющие форму сферы, используемые не для расчёта, а лишь приблизительного построения. Поэтому эти сферы вторичных элементов по своей сути имеют только огибающее действие, что позволяет образовываться новому волновому фронту. Этот принцип хорошо объясняет работу дифракции света, однако решает вопрос только направления фронта, а не объясняет, откуда появляется амплитуда, интенсивность волн, распыление волн и их обратное действие. Френель использовал принцип Гюйгенса для устранения этих недостатков и дополнения его работы физическим смыслом. Через некоторое время учёный представил свою работу, которая полностью подержалась научным сообществом.

Принцип Гюйгенса — Френеля

Ещё во времена Ньютона учёные-физики имели некоторое представление о работе дифракции света, но некоторые моменты оставались для них загадкой из-за небольших возможностей технологий и знаний об этом явлении. Так, описать дифракцию на основе корпускулярной теории света было невозможным.

Независимо друг от друга два учёных разрабатывали качественное объяснение этой теории. Французский физик Френель взялся за дополнение принципа Гюйгенса физическим смыслом, так как изначальная теория была представлена только с математической точки зрения. Таким образом, геометрический смысл оптики изменился с помощью трудов Френеля.

Изменения в принципе выглядели так — Френель физическими методами доказал, что вторичные волны интерферируют в точках наблюдения. Свет может быть замечен во всех участках пространства, где сила вторичных элементов умножается под действием интерференции: так, что если замечается затемнение, можно предположить, волны взаимодействуют и нейтрализуются под влиянием друг друга. В случае если вторичные волны попадают в площадь со схожими типами, состояниями и фазами, то замечается сильный всплеск света.

Таким образом, становится понятным, почему нет обратной волны. Так, когда вторичная волна возвращается обратно в пространство, они вступают во взаимодействие с прямой волной и путём взаимного погашения пространство оказывается спокойным.

Метод зон Френеля

Принцип Гюйгенса — Френеля даёт чёткое представление о возможном распространении света. Применения вышеописанных методов стало называться метод зон Френеля, что позволяет использовать новые и неординарные способы решения задач на нахождение амплитуды. Так, он заменил интегрирование суммированием, что очень положительно приняли в научном сообществе.

На вопросы как работают некоторые важные физические элементы, например, как дифракция света, принцип Гюйгенса — Френеля даёт чёткие ответы. Решение задач стало возможным только благодаря подробному описанию работы этого явления.

Вычисления, представленные Френелем и его методом зон, сами по себе являются трудной работой, однако выведенная учёным формула немного облегчает этот процесс, давая возможность найти точное значение амплитуды. Ранний принцип Гюйгенса не был способен на это.

Необходимо обнаружить на площади точку колебания, которая впоследствии может служить важным элементом в формуле. Площадь будет представлена в виде сферы, так что по методу зон можно разбить её на кольцевые участки, которые позволяют с точностью определить расстояния от краёв каждой зоны. Проходящие по этим зонам точки имеют разное колебание, соответственно, и возникает разница в амплитуде. В случае монотонного убывания амплитуды, можно представить несколько формул:

А рез = А 1 A 2 + A 3 – A 4 +…
А 1 &gt, A 2 &gt, A 3 &gt, A m &gt,…&gt, A ∞

Следует помнить, что довольно большое количество других физических элементов влияют на решение задачи подобного типа, которые тоже нужно искать и учитывать.

Принцип Гюйгенса — Френеля: формулировка, объяснение

Принцип Гюйгенса (от англ. Huygens‑Fresnel principle) — Френеля формулируется следующим образом: каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Другими словами, принцип Гюйгенса-Френеля описывает, как волна распространяется через среду. Он гласит, что каждая точка, достигнутая волной, может рассматриваться как источник новой сферической волны с частотой, равной частоте падающей волны.

Принцип Гюйгенса — Френеля позволяет наглядно и геометрически объяснить такие явления, как отражение. Узнать, более подробно о том, что такое принцип Гюйгенса — Френеля, вы сможете прочитав далее эту статью.

Принцип Гюйгенса — Френеля простыми словами.

В 1678 году Христиан Гюйгенс разработал правило, с помощью которого он хотел описать распространение света. Это правило называется принципом Гюйгенса. Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Построение по принципу Гюйгенса основано на следующих соображениях: каждая точка на волновом фронте распространяющейся волны является центром для сферических или круговых элементарных волн, которые распространяются в той же среде с той же скоростью и частотой, что и исходная волна. Фронт волны, рассматриваемый в более поздний момент времени, называется огибающей всех элементарных волн.

В первоначальной формулировке принципа Гюйгенса рассматривалось распространение элементарных волн только в прямом направлении. Только в 1991 году Дэвид А. Б. Миллер смог решить проблему элементарных волн, распространяющихся в обратном направлении.

Распространение волны

Таким образом, принцип Гюйгенса гласит, что каждая точка на фронте распространяющейся волны может рассматриваться как начальная точка элементарных волн той же частоты и длины волны, которые также распространяются с той же скоростью. Волновой фронт в более поздний момент времени представляет собой огибающую всех элементарных волн.

Но что подразумевается под волновым фронтом и что именно подразумевается под огибающей? Ответ вы найдете в этом разделе статьи. Мы рассмотрим электромагнитные волны, но эти утверждения применимы и к механическим волнам.

Волновой фронт и огибающая

Волна, от которой все точки затем излучают дальнейшие волны, называется первичной волной. Волны, которые излучаются из этих точек, называются элементарными или вторичными волнами.

Возможно, вы знаете, как характеризуется электромагнитная волна. Электромагнитная волна характеризуется пространственным периодом (длина волны), временным периодом (частота), направлением распространения и амплитудой соответствующего компонента поля (это два числа для электрического и магнитного полей). Волна, как правило, представляет собой периодическое явление как в пространстве, так и во времени. Поэтому волне можно присвоить не только временной, но и пространственный период.

Волновой фронт.

Что именно означают эти термины, поначалу не так важно. Важно только, чтобы вы точно знали, что волна делает в определенной точке пространства в определенный момент времени. Колеблется ли она вверх или вниз, насколько высоко она вообще колеблется и так далее. Но это информация только в одной точке.

Но как это будет выглядеть, если, например, оставить точку во времени той же, но немного сместиться перпендикулярно направлению распространения волны. Опять же, вам придется использовать все параметры, чтобы определить, как поведет себя волна в этой точке. Конечно, это относится и ко всем другим точкам, которых можно достичь, перемещаясь в пространстве.

Здесь вам поможет волновой фронт. Волновой фронт соединяет все точки, в которых волна имеет точно такое же поведение в определенный момент времени. Поэтому если вы будете двигаться вдоль фронта волны, поведение волны не изменится. Например, если вы находитесь на гребне волны, то вы всегда будете находиться на гребне точно такой же высоты вдоль соответствующего фронта волны.

Такое «точно такое же поведение в определенное время» иногда можно встретить и под названием «фаза». Здесь важна визуальная информация, которую вы получаете от волновых фронтов. Волновые фронты говорят не только о том, как ведет себя волна, но и в каком направлении она распространяется. Направление распространения волны всегда перпендикулярно волновым фронтам.

Рис. 1. Волновой фронт

Итак, волновой фронт (от англ. wavefront) — набор точек в пространстве с одинаковой фазой колебаний.

Огибающая элементарных волн.

Теперь вы знаете, что такое волновой фронт. Давайте используем эти знания.

Рассмотрим волновой фронт, который имеет форму вертикальной линии. Такой волновой фронт характерен для волны, называемой плоской волной. По этой линии, согласно принципу Гюйгенса — Френеля, каждая точка излучает вторичные волны. Волновые фронты этих вторичных волн представляют собой не линии, а полукруги. Такие волны называются круговыми или сферическими.

Теперь мы ждем определенное время t и затем интересуемся, где будет находиться новый волновой фронт распространяющейся первичной волны. Круговые волновые фронты вторичных волн будут иметь радиус v * t, где v — скорость распространения волны.

Поскольку фронт волны в начале был вертикальной линией, все полукруги вдоль этой линии имеют одинаковую ориентацию. Если теперь провести общую касательную к каждому из этих полукругов, то получится новая вертикальная линия. Эта новая вертикальная линия — просто волновой фронт первичной волны в более поздний момент времени. Вместо «общей касательной к полукругам» вы также найдете более короткое обозначение огибающей всех элементарных волн, иногда просто огибающей.

Если сама первичная волна является не плоской, а круговой, то разница заключается только в ориентации полукругов. Тогда общая касательная будет уже не прямой линией, как вы привыкли видеть в касательных, а кривой линией.

В итоге при построении огибающей вы делаете следующее: вы рисуете пару полукругов, центры которых лежат на волновом фронте первичной волны и радиус которых пропорционален прошедшему времени. Затем находите линию, изогнутую или не изогнутую, которая касается, но не пересекает каждую окружность. Эта линия является огибающей и, следовательно, новым волновым фронтом в более поздний момент времени.

Рис. 2. Огибающая волн

Отражение

Если мы хотим использовать принцип Гюйгенса — Френеля для описания отражения (позже также для преломления), то мы должны внести небольшое изменение в конструкцию огибающей. Центры элементарных волн находятся уже не на волновом фронте первичной волны, а на границе раздела двух сред, с которыми сталкивается первичная волна.

Принцип Гюйгенса сначала был применен к отражению. Волновой фронт падает на граничную поверхность с углом падения θ_e относительно перпендикуляра в точке F. Как мы уже упоминали в разделе о волновом фронте, направление распространения всегда перпендикулярно волновому фронту. Это показано стрелками.

Без наличия граничной поверхности AB волновой фронт CE распространялся бы до волнового фронта JL. Точка E проходит через точки H и L. За время, в течение которого точка E распространяется от H до L, точка D переместится из G в K. В процессе точка D столкнется с фронтом волны JL. При этом точка D сталкивается с пограничной поверхностью в точке I, которая теперь образует центр элементарной волны с радиусом IK. Аналогично, за тот же промежуток времени точка C переместится в F, а затем в J, но столкнется с пограничной поверхностью в точке F.

Поэтому элементарная волна с точкой F в качестве центра будет иметь радиус FJ в тот момент, когда точка E переместится в L. Новый волновой фронт LN может быть построен как касательная к двум окружностям и дает новое направление распространения (нормаль к волновому фронту LN). Отраженная волна распространяется с углом отражения θ_r относительно перпендикуляра.

Рис. 3. Отражение волн, согласно принципа Гюйгенса — Френеля

Преломление

Изменение показателя преломления приводит к изменению скорости распространения. Поэтому радиус элементарных волн в области с показателем преломления n₂ также изменяется. Именно это изменение приводит к наблюдению преломления, которое мы покажем вам в этом подразделе.

Для этой цели мы произвольно предполагаем, что показатель преломления n₂ больше показателя преломления n₁. Больший показатель преломления среды сопровождается меньшей скоростью распространения волны в этой среде. Без границы раздела AB волновой фронт CE превратился бы в волновой фронт JL, когда точка E достигла бы точки L.

В случае отражения элементарная волна вокруг точки F, после того как точка E переместилась в L, будет иметь радиус r₁. Поскольку мы предположили n₂ > n₁, радиус r₂ элементарной волны во второй среде меньше радиуса r₁ той же элементарной волны в первой среде в n₁ / n₂ раз.

Поэтому построение нового волнового фронта во второй среде аналогично построению в случае отражения. Единственное отличие заключается в том, что круги имеют меньший радиус. Это снова приводит к новому волновому фронту LN волны во второй среде как касательной к двум окружностям. Вы также получите новое направление распространения, нарисовав вертикальные линии на этом волновом фронте. Преломленная волна распространяется во второй среде под углом θ_t относительно перпендикуляра в точке F. Видно, что этот угол меньше, чем перпендикуляр в точке F. Вы можете видеть, что этот угол меньше угла отражения. Причиной этого является именно более низкая скорость распространения из-за более высокого показателя преломления.

Рис. 4. Преломление волн, согласно принципа Гюйгенса — Френеля

Дифракция

Наконец, мы покажем вам, как принцип Гюйгенса — Френеля помогает нам геометрически объяснить дифракцию волн.

Для этого предположим, что мы смотрим на плоскую волну, попадающую в отверстие. Интерес представляет только та часть волнового фронта, которая находится внутри отверстия. Волновой фронт за пределами отверстия «заблокирован» и поэтому не имеет значения.

Теперь принцип Гюйгенса — Френеля предписывает нам выбрать точки вдоль волнового фронта внутри отверстия, которые действуют как центры для элементарных волн. Мы произвольно выбираем несколько точек и рисуем фронты круговых волн для нескольких различных моментов времени.

Аналогично, принцип Гюйгенса — Френеля гласит, что новый волновой фронт первичной волны в более позднее время является просто огибающей элементарных волн. Поэтому в какой-то момент мы перестаем рисовать полукруги и ищем линию, которая касается всех окружностей, но не пересекает их. Эта линия и есть искомый волновой фронт. Если теперь вы проведете еще несколько линий перпендикулярно фронту волны, вы найдете направление распространения волны после открытия. Что вы видите? Волна после открытия, кажется, распространяется в области, которые не лежат на прямолинейном движении плоской волны. И именно это отклонение от «прямолинейного движения» называется дифракцией. Вы также можете встретить термин «волна распространяется в геометрической тени».

Все это в конечном итоге означает следующее: если расширить отверстие до прямоугольника, то все, что находится за пределами этого прямоугольника, называется «геометрической тенью». Теперь, если вместо плоской волны представить горизонтальные линии, указывающие направление распространения, то можно ожидать, что они останутся внутри прямоугольника. Но это не так, и такое наблюдение называется дифракцией. Принцип Гюйгенса — Френеля позволяет наглядно объяснить это наблюдение.

Рис. 5. Дифракция волн, согласно принципа Гюйгенса — Френеля

Описание и применение принципа Гюйгенса — Френеля

Принцип Гюйгенса

Работу подобного явления описал Христиан Гюйгенс. После определённого количества проведённых экспериментов со световыми волнами на водной поверхности, он предложил науке новое объяснение такого феномена и дал ему название «волновой фронт». Таким образом, Христиан дал возможность понять, как будет вести себя луч света при попадании на какую-то поверхность другого типа.

Его принцип звучит следующим образом: