Умножение числа на 0: что такое умножение, свойства 0, можно ли делить на 0

Таблица умножения на 0

При умножени любого числа на 0 результат всегда будет равнятся 0.

0×

Множители			Произведение (Результат)
	×	1	=
	×	2	=
	×	3	=
	×	4	=
	×	5	=
	×	6	=
	×	7	=
	×	8	=
	×	9	=
	×	10	=

Рассмотрим пример:

0 + 0 + 0 + 0 + 0 = 0

В равенстве все слагаемые одинаковые, а занчит сложение можно заменить умножением.

0 + 0 + 0 + 0 + 0 = 0 × 5 = 0

При умножении нуля на любое число получается 0.

Дополнительная таблица до 100

0×

Множители			Произведение (Результат)
	×	11	=
	×	12	=
	×	13	=
	×	14	=
	×	15	=
	×	16	=
	×	17	=
	×	18	=
	×	19	=
	×	20	=
	×	21	=
	×	22	=
	×	23	=
	×	24	=
	×	25	=
	×	26	=
	×	27	=
	×	28	=
	×	29	=
	×	30	=
	×	31	=
	×	32	=
	×	33	=
	×	34	=
	×	35	=
	×	36	=
	×	37	=
	×	38	=
	×	39	=
	×	40	=
	×	41	=
	×	42	=
	×	43	=
	×	44	=
	×	45	=
	×	46	=
	×	47	=
	×	48	=
	×	49	=
	×	50	=
	×	51	=
	×	52	=
	×	53	=
	×	54	=
	×	55	=
	×	56	=
	×	57	=
	×	58	=
	×	59	=
	×	60	=
	×	61	=
	×	62	=
	×	63	=
	×	64	=
	×	65	=
	×	66	=
	×	67	=
	×	68	=
	×	69	=
	×	70	=
	×	71	=
	×	72	=
	×	73	=
	×	74	=
	×	75	=
	×	76	=
	×	77	=
	×	78	=
	×	79	=
	×	80	=
	×	81	=
	×	82	=
	×	83	=
	×	84	=
	×	85	=
	×	86	=
	×	87	=
	×	88	=
	×	89	=
	×	90	=
	×	91	=
	×	92	=
	×	93	=
	×	94	=
	×	95	=
	×	96	=
	×	97	=
	×	98	=
	×	99	=
	×	100	=

Как быстро и легко выучить таблицу умножения?

Первое, что нужно для начала изучения таблицы умножения — это иметь перед глазами саму таблицу. Лучше, если обучение будет проходить по таблице умножения Пифагора, потому как приведённая выше таблица это лишь столбик, в котором число 0 умножают на различные числа. В данном случае невозможно объяснить логические связи между цифрами и закономерности между ними, поэтому ребёнку придётся заучить данный столбик наизусть, как стихотворение. Мы же рекомендуем начинать изучение таблицы умножения по таблице Пифагора.

Перед началом изучения таблици умножения рекомендуем ознакомиться с материалом: как быстро и легко выучить таблицу умножения. Не тратьте свои нервы и нервы своего ребёнка.

Таблицу умножения Пифагора можно использовать на нашем сайте, а также скачать её или распечатать.

Умножение на ноль – правило в математике и примеры

Правило арифметики о том, что при умножении на ноль любого числа получается 0, изучают еще в младших классах средней школы. Дети верят учителям на слово, но при взрослении у многих возникает интерес к этой теме. Людям хочется больше узнать, почему с нулем связаны разные ограничения. Математики объясняют подобные факты свойствами этой удивительной цифры.

• История возникновения
• Сложение, умножение, степень
• Деление на ноль
• Раскрытие неопределенностей

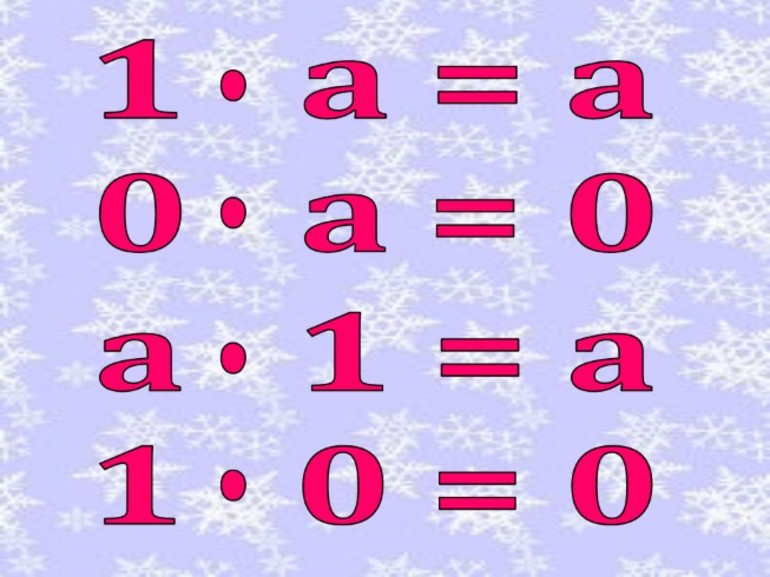
История возникновения

Ноль означает ничто, пустоту. Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.

Но повсеместно применять в вычислениях его начали лишь спустя несколько тысячелетий. Это произошло в Индии. Нулю там придавали не только математический, но и философский смысл. Он означает отсутствие всего, а его форма соответствовала кругу жизни.

Индусы использовали 0 как любое другое число. Его складывали, вычитали, на него умножали. С делением на 0 возникла проблема, но благодаря ей в дальнейшем возникла другая область математики — математический анализ. Идею использования нуля подхватили исламские ученые на Ближнем Востоке и внесли его в арабскую систему счисления.

В Европе до Крестовых походов применялась Римская система счисления. Это непозиционная система, и ноль в ней отсутствует. Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.

Во времена первых Крестовых походов арабские цифры вместе с нолем и позиционной системой счисления пришли в Европу. К этим новшествам сначала отнеслись с большим недоверием. Во Флоренции даже был издан закон о запрещении использования арабских цифр вместе с нулем.

Считалось, что они поощряют мошенничество: 0 легко переделать на цифру 9 или приписать в конце счета, чтобы величина долга возросла многократно. Лишь в XV веке, когда началось развитие в сфере математики и механики, люди оценили преимущество нуля и арабских цифр и стали использовать их повсеместно.

Сложение, умножение, степень

В математике используется несколько действий. Они следующие:

• сложение;
• вычитание;
• умножение;
• деление;
• возведение в степень.

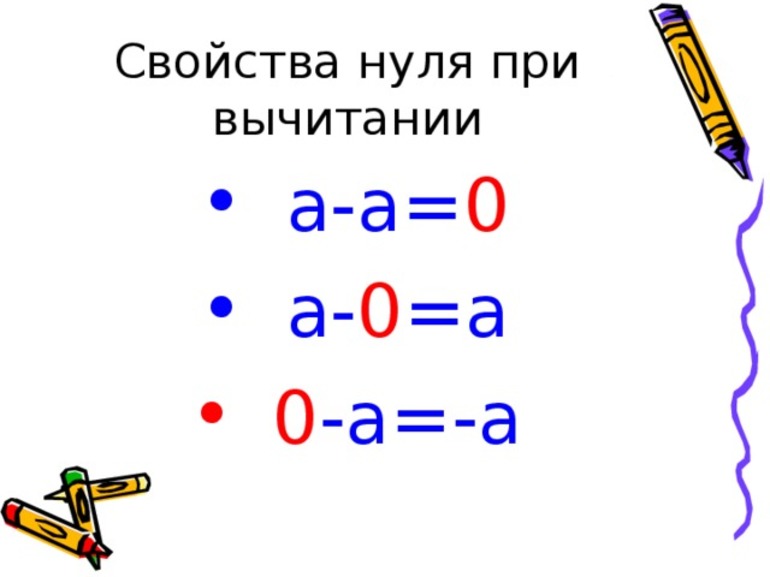
Сложение с нулем обычно вопросов не вызывает. Если к любому числу добавить 0, это значит, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй. То же самое будет, если отнять ноль.

Операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на ноль получается ноль. Это объясняется особенностями операции умножения. Изначально ее определяли как число, прибавленное к самому себе определенное количество раз, что справедливо для натуральных чисел. Так, 5 х 3 = 15. Этот пример можно заменить следующим выражением: 5 + 5 + 5 = 15. То есть число 5 было взято 3 раза. Согласно этому правилу, умножение на 0 числа 5 дает нулевой результат, и 5 х 0 = 0.

Чтобы было нагляднее, можно привести следующий пример:

• если мальчик съел 2 раза по 2 яблока, то окажется, что он позавтракал 4 яблоками;
• если он съел 3 раза по 2 яблока, то в результате получится 6 яблок;
• если же он съел 0 раз по 2 яблока, то ответ будет 0.

Иногда юные скептики выдвигают следующее возражение: допустим, у мальчика в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся в него в руке. Почему же тогда результат равен нулю? Действительно, яблоки из руки никуда не денутся. Но в примере учитываются лишь те из них, которые были съедены, проще говоря, оказались в желудке у мальчика. В последнем случае они туда не попали.

Правило умножения на ноль в математике действительно для любых чисел:

• положительных;
• отрицательных;
• целых;
• дробей;
• разрядных;
• рациональных;
• иррациональных;
• 0 можно умножать на 0.

В любом случае произведение будет нулевым. С нулем можно производить следующие действия:

1. Если его разделить на любое ненулевое число, то в результате получится ноль. Правило действительно для положительных и отрицательных чисел.
2. Любое число, не равное нулю, можно возвести в нулевую степень, в результате получится 1. Ноль в нулевую степень возводить нельзя, это бессмысленно.
3. Нуль можно возвести в любую ненулевую степень, получится нуль. Пример: 0 2 = 0. Это выражение можно заменить следующим: 0 х 0 =0. Результат будет нулевым согласно правилам умножения.
4. Корень из нуля равен нулю.

Деление на ноль

Математики говорят, что четыре арифметических действия: сложение, вычитание, умножение и деление неравноправны. Базовыми считаются первое и третье из них (сложение и умножение), а деление и вычитание — производными.

Например, разность между 5 и 2 равна 3. Это действие также можно записать в виде следующего выражения: Х + 2 = 5. Решением уравнения будет число 3. Аналогичное правило действует и для умножения. Деление 6 на 3 можно записать так: Х * 2 = 3.

Для действий с нулем можно использовать следующий прием. Выражение записывают так: Х * 0 = 0. Здесь X может быть равен любому числу. Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.

Если попытаться найти результат от деления ненулевого числа (например, 5) на ноль, то это действие можно записать так: Х * 0 = 5. Так, при умножении любого числа на ноль получается ноль, у этого уравнения в арифметике нет решения.

Раскрытие неопределенностей

Действиями, связанными с делением на 0, занимается один из разделов высшей математики — математический анализ. В нем используется такое понятие, как бесконечность (бесконечно большая величина). Одно из ее определений — это предел, к которому стремится выражение а/Х при Х, стремящемся к нулю. Здесь а — любое ненулевое действительное число. Если в этом выражении уменьшать значение X, то результат будет увеличиваться, пока, в конце концов, не подойдет к бесконечности. С этой величиной можно делать различные математические действия:

• прибавлять любые числа;
• вычитать числа, не равные бесконечности;
• умножать на значения, не равные 0 и бесконечности;
• возводить в степень, не равную 0.

В результате получится бесконечность. Следующие выражения дают в результате полную неопределенность:

• бесконечность минус бесконечность;
• бесконечность умножить на 0;
• бесконечность разделить на бесконечность;
• ноль разделить на ноль;
• ноль умножить на бесконечность;
• ноль в нулевой степени;
• бесконечность в степени ноль;
• единица в степени бесконечность.

Задачи с неопределенностями возникают при вычислении пределов функций, которые заданы формулами, дающими подобные выражения при подстановке предельных значений аргумента. Математики говорят, что результатом таких уравнений будет бесконечное множество чисел. Обычно для их решения используют различные схемы и алгоритмы. Это называется раскрытием неопределенности.

Над нулем можно проделывать все арифметические операции. Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.

Уроки математики: умножение на ноль – главное правило

Впервые с таким арифметическим действием, как умножение, ученики знакомятся на школьной скамье. Учитель математики среди многочисленных правил поднимает тему «умножение на ноль». Несмотря на однозначность формулировки, у учащихся возникает множество вопросов. Давайте рассмотрим, что будет, если умножить на 0.

По две стороны спора

Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности.

В первую очередь акцентируется внимание на отсутствии достаточного уровня знаний у учеников средней общеобразовательной школы. Переступая порог учебного заведения, участник образовательного процесса в большинстве случаев не задумывается о главной цели, которую необходимо преследовать.

Это интересно! Как раскрыть модуль действительного числа и что это такое

В течение обучения преподаватель освещает различные вопросы. В их число входит ситуация, что получится, если умножать на 0. Стремясь предвосхитить повествование преподавателя, некоторые ученики вступают в полемику. Они доказывают, по крайней мере, стараются, что умножение на 0 допустимо. Но, к сожалению, это не так. При умножении на 0 любого числа получается ровным счетом ничего. В некоторых литературных источниках даже встречается упоминание, что любое число, умноженное на ноль, образует пустоту.

Важно! Внимательные слушатели аудитории сразу схватывают, что если число умножить на 0, то в результате получится 0. Иное развитие событий прослеживается в случае тех учеников, кто систематически пропускает занятия. Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.

В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации.

Различие во взглядах на тему спора заключается в степени образованности на предмет того, можно умножать на 0 или все-таки нет. Единственный допустимый выход из сложившейся ситуации – попытаться воззвать к логическому мышлению для поиска верного ответа.

Для объяснения правила не рекомендуется использовать следующий пример. У Вани в сумке лежат 2 яблока на перекус. В обед он задумался о том, чтобы положить в портфель еще сколько-нибудь яблок. Но в тот момент рядом не оказалось ни одного фрукта. Ваня не положил ничего. Иными словами, к 2 яблокам он поместил 0 яблок.

Это интересно! Считаем правильно: как находить процент от суммы и числа

В плане арифметики в данном примере получается, что если 2 умножить на 0, то не получается пустоты. Ответ в этом случае однозначный. Для этого примера правило умножения на ноль не актуально. Верное решение заключается в суммировании. Именно поэтому правильный ответ заключается в 2 яблоках.

В противном случае учителю не остается ничего иного, кроме как составить ряд заданий. Последняя мера – повторно задать прохождение темы и провести опрос на исключения в умножении.

Суть действия

Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия.

Сущность действия умножить изначально определялась исключительно для натурального числа. Если раскрывать механизм действия, то определенное число, участвующее в вычислении, прибавляется к самому себе.

При этом важно учитывать количество прибавлений. В зависимости от данного критерия получается различный результат. Прибавление числа относительно самого себя определяет такое его свойство, ка натуральность.

Это интересно! Как разложить на множители квадратный трехчлен: формула

Рассмотрим на примере. Необходимо число 15 умножить на 3. При умножении на 3 число 15 троекратно увеличивается в своей величине. Иными словами, действие выглядит как 15 * 3 = 15 + 15 + 15 = 45. Основываясь на механизме расчета, становится очевидным, если число умножить на другое натуральное число, возникает подобие сложения в упрощенном виде.

Алгоритм действий при умножении на 0 целесообразно начинать с предоставления характеристики на ноль.

Обратите внимание! Согласно общепринятому мнению ноль обозначает целое ничто. Для пустоты подобного рода в арифметике предусмотрено обозначение. Несмотря на данный факт, нулевое значение не несет под собой ничего.

Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.

Иными словами, если умножить на ноль, то получится многообразие вариантов. В нулевом значении ученые рассматривали некое подобие глубины мироздания.

В качестве подтверждения возможности умножить на 0 математики приводили следующий факт. Если рядом с любым натуральным числом поставить 0, то получится значение, превышающее исходное в десятки раз.

Приведенный пример является одним из аргументов. Кроме доказательства подобного рода, существует множество других примеров. Именно они лежат в основе непрекращающихся споров при умножении на пустоту.

Это интересно! Как найти и чему будет равна длина окружности

Целесообразность попыток

Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой.

По существу от таких попыток ничего не произойдет, но и пользы не будет. Если произвести умножение на нулевое значение, то получится в дневнике неудовлетворительная отметка.

Единственная мысль, которая должна возникать при умножении на пустоту, – невозможность действия. Запоминание в данном случае играет немаловажную роль. Выучив правило раз и навсегда, учащийся предотвращает появление спорных ситуаций.

В качестве примера, применяемого при умножении на нулевое значение, разрешается использовать следующую ситуацию. Саша решила купить яблоки. Пока она была в супермаркете, она остановила выбор на 5 крупных спелых яблоках. Сходив в отдел молочной продукции, она посчитала, что этого ей будет недостаточно. Девочка положила к себе в корзину еще 5 штук.

Поразмыслив еще чуть-чуть, она взяла еще 5. В результате на кассе у Саши получилось: 5 * 3 = 5 + 5 + 5 = 15 яблок. Если бы она положила по 5 яблок только 2 раза, то было бы 5 * 2 = 5 + 5 = 10. В том случае, если бы Саша не положила в корзинку ни разу по 5 яблок, было бы 5 * 0 = 0 + 0 + 0 + 0 + 0 = 0. Иными словами, купить яблоки 0 раз значит не купить ни одного.

Полезное видео

Подведем итоги

Правило умножения на нулевое значение порождает множество споров. Для понимания его сути достаточно рассмотреть пару примеров. Только запоминание формулировки позволит уяснить, можно умножать на 0 или нет.

Правила умножения и деления любого числа на ноль

Число ноль занимает особое место в такой науке, как математика, даже несмотря на то, что оно буквально означает «ничто», «пустоту».

Ноль используют для обозначения «пустых» разрядов в десятичных дробях, как после запятой, так и до, для начала отсчёта координат в системах координат, а также именно нолю принадлежит одно из основных правил арифметики – на ноль делить нельзя.

С ним выполняются все арифметические действия: деление, умножение, сложение и вычитание, но именно деление и умножение на ноль мы сейчас рассмотрим подробнее, так как в них содержатся некоторые нюансы.

Что такое умножение в математике, определение.

Для того, чтобы разобраться, чем отличается умножение числа на ноль от умножения других чисел на друг друга, нужно для начала дать определение, что такое операция умножения в целом.

Умножение – одно из основных действий в математике, в котором участвуют два аргумента – множитель и сомножитель. Зачастую, особенно в школах, первый аргумент называют множимым, а второй множителем. Результат их умножения называют произведением.

Для натуральных чисел умножением, по сути, является многократное сложение. Таким образом получаем, чтобы умножить число a на число b, необходимо b раз сложить a.

a ⋅ b = a + a + … + a> b

Умножение на ноль, правило математики.

Основное правило гласит: при умножении числа на ноль и ноль на число в ответе всегда будет получаться ноль.

a ⋅ 0 = 0

⋅ a = 0

Не всегда всем понятно, почему же в итоге получается ноль. Правило сухо заучивается, а вопрос так и остается без ответа, хотя ничего сверхъестественного и скрытого в этом нет, всё многим проще, чем может показаться изначально.

Ответ кроется в самом действии умножения, о котором мы подробно поговорили выше. Рассмотрим самое логичное и примитивное объяснение, дабы понять, что данное умножение бесполезно, так как при умножении числа на ноль результат всё равно будет один – ноль.

Допустим, число a – это яблоко, а число b – это количество яблок, которое необходимо взять. Если b будет равняться нолю, получается, мы берем яблоко ноль раз, а, следовательно, как не было яблок, так и нет.

И наоборот, если у нас нет яблок, то и взять ничего не получится.

Данный пример – настолько простой и понятный в понимании правил умножения на ноль, что даже самый далёкий от математических формул человек сможет в своей голове всё по полочкам разложить.

Примеры умножения на ноль.

0 ⋅ 3 = 0 + 0 + 0 = 0

0 ⋅ 4 = 0 + 0 + 0 + 0 = 0

Что такое деление в математике, определение.

Деление – в математике действие обратное умножению, также состоящее из двух аргументов – делимого и делителя. Результат деления называют частным. Остатком называют то число, что осталось после деления делимого на делитель.

Деление в математике принято обозначать двоеточием :, косой чертой /, горизонтальной чертой – или обелюсом ÷.

Если умножение для натуральных чисел заменяет многократное сложение, то, соответственно, деление будет заменять многократное вычитание.

Чтобы стало понятнее, рассмотрим на простом примере, таком как деление числа15 на число 2.

Из действия вычитания мы находим, что число 2 содержится в 15 семь полных раз, и еще остается единица.

В данном случае 15 – делимое, 2 – делитель, 7 – неполное частное, а 1 – остаток.

Также иногда результат деления называют отношением.

Деление на ноль, правило математики.

С начальной школы всем пытаются привить, что на ноль делить нельзя. Все это заучивают, не требуя лишних доказательств, ну нельзя и нельзя. Однако стоит спросить взрослого человека – а почему, собственно, нельзя? Мало кто сможет достаточно внятно ответить на поставленный вопрос из школьной программы, так как это правило вызывает довольно много противоречий.

Большинство людей и правда не делит на ноль только исходя из этого правила, не пытаясь найти ответ, по которому станет понятен этот запрет. Хотя ответ лежит прямо перед глазами.

Как оказалось, не все действия в арифметике полноправны, а точнее только сложение и умножение, следовательно, все остальные действия с числами исходят от них.

Рассмотрим в качестве примера выражение: 14 : 0

Данное выражение можно представить и в виде уравнения: ⋅ x = 14

Становится понятно, что при делении на ноль, необходимо найти такое число, при умножении на которое получится 14, а это априори невозможно исходя из всего того, что мы выяснили ранее.

Умножение числа нуль и на нуль. Деление нуля

Тема: «Умножение числа нуль и на нуль. Деление нуля».

Цель: познакомить с правилом умножения числа 0 и на 0, деления 0;закреплять знание таблицы умножения, умение решать задачи изученных видов; учить рассуждать и делать выводы.

Планируемые результаты: учащиеся научатся выполнять умножение 0 на число, число на 0, делить 0; пользоваться таблицей умножения и деления; решать задачи изученных видов; оценивать правильность выполнения действий.

Оборудование: карточки для игры “Почтальон”; таблица с геометрическими фигурами, раздаточный материал, персональный компьютер, медиа-проектор, учебник «Математика» М. Н. Перова (4 класс).

Тип урока: новая тема.

Вид урока: урок-игра.

Ход урока

Проверка домашнего задания.

Учитель: вспоминаем табличное умножение и деление. Сейчас мы поиграем в игру “Почтальоны”. Света, ты будешь почтальоном. На доске домики с номерами. Твоя задача – взять пример-письмо, правильно его решить и определить в какой дом нам нужно отнести письмо.

3х4 2х2 9х2 3х1 3х8 25:5

Учитель: вставьте пропущенный знак действия.

III. Знакомство с новым материалом

Напрасно думают, что ноль

Играет маленькую роль,

Когда-то многие считали

Что ноль не значит ничего

И, как ни странно полагали

Что он совсем не есть число.

Но о его особых свойствах

Мы поведем теперь рассказ

Коль ноль к числу ты прибавляешь

Иль отнимаешь от него

В ответе тотчас получаешь

Опять то самое число

Попав как множитель средь чисел

Он мигом сводит все на нет

И потому в произведенье

Один за всех несет ответ

А относительно деленья

Нам твердо помнить нужно то,

Что уж давно в научно мире

Делить на ноль запрещено

И впрямь: какое из известных

Число за частное нам взять

Когда с нулем в произведенье

Все числа ноль лишь могут дать

Учитель: Давай проверим,все ли в стихотворении правильно:

Учитель: применим переместительное свойство умножения и заменим умножение сложением: 7•0=0•7=0+0+0+0+0+0+0=0

Учитель: мы знаем, что деление проверяется умножением: тогда частное умножим на 0 – должно получиться 7, но это не возможно! Какое бы число мы не умножали на 0, всегда в произведении будет 0.

V. Закрепление изученного материала

1. Решение задачи (с. 143 № 7)

Учитель: о чем говорится в задаче?

Ученик: о ремонте, фундаменте, кирпичах.

Учитель: что нужно узнать?

Ученик: сколько кирпичей осталось уложить.

Учитель: сможем ли мы сразу ответить на этот вопрос?

Ученик: потому что мы не знаем, сколько кирпичей рабочий использовал.

Учитель: сможем ли мы это узнать?

Учитель: каким действием?

Ученик: делением.

Учитель: сможем ли мы теперь ответить на вопрос задачи?

Учитель: каким действием?

Учитель: сколько же кирпичей осталось уложить рабочему?

Ученик: (40:5=8, 40-8=32) 32 кирпича.

2. Самостоятельная работа (с. 144 № 18)

3. Работа у доски (с. 144 № 11)

1. Круговые примеры

Учитель: Мы будем лесниками. Нам надо определить высоту некоторых деревьев, для этого необходимо решить круговые примеры.

2. Арифметический диктант

Учитель: А сейчас будем стенографистами. Я диктую, а ты записываешь – стенографируешь с помощью карточек.

• Сумму чисел 45 и18 (45+18=63)

• Произведение чисел 8 и 3 (8*3=24)

• Разность чисел 35 и 7 (35-7=22)

• Частное чисел 20 и 4 (20:4=5)

3. Геометрический материал.

Учитель: последнее задание. Какие геометрические фигуры вы видите?

Посчитайте и скажите, сколько раз встречается каждая фигура.

(Круг – 12, квадрат – 6, треугольник – 6, прямоугольник – 5.)

Самостоятельное выполнение с. 144 № 17 (1,2 ст.).Ответы записаны на доске:0,0,0;5,5,5.

Оцени свою работу на уроке смайликом.

VIII. Домашнее задание

Дидактический материал по математике для учащихся 5 класса по теме «Умножение десятичных дробей на 10,100,1000» Определите, можно ли к данному объекту применить правило умножение и деления десятичных дробей на 10,100,1000 и т. д. Объект признаки Вывод.

Конспект НОД по математике в старшей группе «Деление квадрата на части» Программные задачи: Закрепить счет в пределах 10 (прямой и обратный). Находить последующее, предыдущее число. Закрепить умение детей изготавливать.

«Деление предметов на несколько частей». Конспект НОД по ОО «Познание» Конспект НОД «Познавательное развитие» (Формирование элементарных математических представлений, физическая культура, художественное творчество.

Конспект урока математики в 6 классе на тему «Нахождение дроби от числа и числа по значению его дроби» Конспект урока математики в 6 классе МОУ СОШ с. Телегино Колышлейского района Пензенской области на тему “Нахождение дроби от числа и числа.

Методическая разработка урока математики на тему «Умножение на двузначное число» в 3 классе Математика 3 класс Шугайлова Светлана Владимировна, МБОУ гимназия №19 Петерсон, Л. Г. Математика. 3 класс: учебник / Л. Г. Петерсон. – М. :.

Конспект урока математики в 6 классе «Умножение рациональных чисел» Тема урока: Умножение положительных и отрицательных чисел. 6 класс Цели урока: создать условия для вывода правила умножения рациональных.

Технологическая карта урока математики в 3 классе в соответствии с требованием ФГОС «Деление с остатком» Этап урока Содержание заданий (для учащихся) Виды деятельности, формы организации работы Планируемые результаты Предметные Личностные, метапредметные.

Урок русского языка в 1 классе «Деление слов на слоги» Тема: «Деление слов на слоги» Цель: формировать умения делить слова на слоги, анализировать модели слов, находить слова по данным моделям.

Урок математики в 3 классе «Умножение суммы на число» УМК «Школа России» муниципальное бюджетное общеобразовательное учреждение «Ивановская основная школа» Проект урока по математике.

Урок математики в 4 классе по теме «Деление на трехзначное число» Тема: Деление на трехзначное число Цель: закрепление умения делить многозначные числа на трехзначное с использованием алгоритма деления.

Почему делить на ноль нельзя?

Информация о том, что на ноль делить нельзя, известна нам со школьной скамьи. Мы усваиваем это правило раз и навсегда. Однако лишь некоторые из нас задаются вопросом, а почему собственно нельзя это делать. Но ведь знать и понимать причины невозможности этого действия важно, так оно раскрывает принципы «работы» и других математических операций.

Все математические действия равны, но некоторые равнее других

Начнём с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не являются равноправными. И разговор идёт не о порядке выполнения действий при решении какого-нибудь примера или уравнения. Нет, имеется в виду само понятие числа. И согласно ему, наиболее важными являются сложение и умножение. А уже вычитание и деление «вытекают» из них тем или иным образом.

Сложение и вычитание

Например, разберём простую операцию: «3 – 1». Что это означает? Школьник легко объяснит эту задачку: это означает, что было три предмета (например, три апельсина), один вычли, оставшееся количество предметов и есть верный ответ. Верно описано? Верно. Мы и сами объяснили бы точно так же. Но математики рассматривают процесс вычитания иначе.

Операция «3 – 1» рассматривается не с позиции вычитания, а только со стороны сложения. Согласно этому нет никаких «три минус один», есть «какое-то неизвестное число, которое при прибавлении одного даёт три». Таким образом, простое «три минус один» превращается в уравнение с одним неизвестным: «х + 1 = 3». Причём появление уравнения изменило знак — вычитание поменялось на сложение. Осталась только одна задача — отыскать подходящее число.

Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики и примеры решения типовых задач. В конце книги помещен предметный указатель.Пособие будет полезно учащимся 7-11 классов, абитуриентам, студентам, учителям/

Умножение и деление

Аналогичные метаморфозы происходят с таким действием, как деление. Задачу «6 : 3» математики отказываются воспринимать как некие шесть предметов, разбитых на три части. «Шесть разделить на три» не что иное, как «неизвестное число, умноженное на три, в результате чего получилось шесть»: «х · 3».

Делим на ноль

Выяснив принцип математических действий по отношению к задачам с вычитанием и делением, рассмотрим наше деление на ноль.

Задача «4 : 0» превращается в «х · 0». Получается, нам нужно найти такое число, умножение с которым даст нам 4. Известно, что умножение на ноль всегда даёт ноль. Это уникальное свойство нуля и, собственно, его суть. Числа, умноженного на ноль и выдающего любое другое число кроме нуля, не существует. Мы пришли к противоречию, значит задача не имеет решения. Следовательно, записи «4 : 0» не соответствует никакое определённое число, а отсюда уже вытекает её бессмысленность. Поэтому, чтобы кратко подчеркнуть непродуктивность такого процесса, как деление на ноль, и говорят, что «на ноль делить нельзя».

Больше интересных материалов:

А что получится, если ноль разделить на ноль?

Представим такое уравнение: «0 · x = 0». С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0 : 0 = 0».

Однако теперь давайте в это же уравнение с неизвестным вместо «x = 0» подставим любое другое число, например «x = 7». Получившееся выражение выглядит теперь как «0 · 7 = 0». Вроде бы, всё верно. Делаем обратную операцию и получаем «0 : 0 = 7». Но тогда, получается, что можно взять абсолютно любое число и вывести 0 : 0 = 1, 0 : 0 = 2. 0 : 0 = 145. — и так до бесконечности.

Если при любом числе х уравнение будет справедливо, то мы не имеем права выбрать лишь одно, исключив остальные. Значит, мы так и не можем ответить, какому числу соответствует выражение «0 : 0». Снова оказавшись в тупике, мы признаём, что и эта операция тоже бессмысленна. Получается, что ноль нельзя делить даже на самого себя.

Оговоримся, что в математическом анализе иногда бывают специальные условия задачи — так называемое «раскрытие неопределенности». В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит.