Урок 48. Функции. Свойства функций и их графики. Исследование функций
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
у – зависимая переменная, значение функции
Определение
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Определение
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
- для любого х из области определения выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Определение
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х12, выполняется неравенство у12.
Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких что, х12, выполняется неравенство у1>у2.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Дополнительная литература:
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции

1) Область определения функции
Знаменатель дроби не равен нулю:

Получили область определения

D(y)=
- Множество значений функции
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).



Получили
- Четность / нечетность функции

D(y)= – симметрична относительно нуля

,
следовательно, функция четная и ее график симметричен относительно оси ОУ

Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
- Промежутки знакопостоянства

у>0 при

Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.
Определим знаки производной в полученных промежутках.

точки -1, 1 – выколоты, 0 – закрашена

Производная положительна, а значит, функция возрастает при .

Производная отрицательна, а значит, функция убывает при
х=0 – стационарная точка.
В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.
Значение функции в точке максимума

- Дополнительные точки
- Отразим найденные свойства графически, построим график функции

2. Решение задачи на оптимизацию
Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.
В решении таких задач выделяют 3 основных этапа:
1 этап. «Перевод» задачи на язык функций:
- вводят независимую переменную х
- выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
- выражают у через х и другие известные величины
- устанавливают по условию задачи границы изменения переменной х
2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.
Рассмотрим план решения на примере задачи.
Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t 2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t 2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x 2 у.е.
Тогда на 2 объект направлено (24 – x) рабочих – суточная заработная плата (24 – x) 2 (у.е.)
Всем рабочим нужно заплатить 4x 2 +(24 – x) 2 = 5x 2 -48x+576 (у.е.)
Причем 0≤ x ≤ 24, x ϵ N.
Рассмотрим функцию f(x)=5x 2 -48x+576.
Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x = 4,8 .
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.

область определения – множество действительных чисел – симметрична относительно нуля
у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, – симметричен относительно оси ОУ и относительно начала координат.
Данная функция одновременно четна и нечетна.
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
логарифмируемое выражение должно быть положительным
Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, – функция общего вида.
Найдем область определения D(f)


Проверим второе условие

Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
Зайдем с другого конца, выразим -f(x):

домножим на сопряженное


Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
Четность / нечетность
и четная, и нечетная


2.
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у

Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:
Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.
Выполним построения выделенных функций.

Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.
Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.

Ответ:
Понятие функции. Основные свойства функции
Под множеством понимается совокупность однородных объектов. Объекты, которые образуют множество, называются элементами или точками этого множества. Множества обозначают прописными буквами, а их элементы – строчными. Если a является элементом множества A, то используется запись aÎA. Если b не является элементом множества A, то это записывается так: b ÏA. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается так: Ø.
Если множество B состоит из части элементов множества A или совпадает с ним, то множество B называют подмножеством множества и обозначают BÌA.
Два множества называют равными, если они состоят из одних и тех же элементов.
Объединением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих хотя бы одному из множеств: C=AÈB.
Пересечением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих каждому из данных множеств: C=AÇB.
Разностью множеств A и B называется множество E, состоящее из всех элементов множества A, которые не принадлежат множеству B: .
Дополнением множества AÌB называется множество C, состоящее из всех элементов множества B, не принадлежащих A.
Множества, элементами которых являются действительные числа, называются числовыми:
| R – множество действительных чисел; Q – множество рациональных чисел; I – множество иррациональных чисел; | Z – множество целых чисел; N – множество натуральных чисел. |
При этом NÌZÌQÌR, IÌR и R=IÈQ.
Множество X, элементы которого удовлетворяют неравенству называется отрезком (сегментом) и обозначается [a; b]; неравенству axb – интервалом и обозначается () ; неравенствам и – полуинтервалами и обозначаются соответственно и . Также часто приходится иметь дело с бесконечными интервалами и полуинтервалами: , , , и . Все их удобно называть промежутками .
Интервал , т.е. множество точек удовлетворяющих неравенству (где ), называется -окрестностью точки a.
Понятие функции. Основные свойства функции
Если каждому элементу x множества X ставится в соответствие единственный элемент y множества Y, то говорят, что на множестве X задана функция y=f(x). При этом x называют независимой переменной или аргументом, а y – зависимой переменной или функцией, а f обозначает закон соответствия. Множество X называют областью определения функции, а множество Y – областью значений функции.
Существует несколько способов задания функций.
1) Аналитический способ – функция задается формулой вида y=f(x).
2) Табличный способ – функция задается таблицей, содержащей значения аргумента и соответствующие им значения функции y=f(x).
3) Графический способ – изображение графика функции, т.е. множества точек (x; y) координатной плоскости, абсциссы которых представляют значения аргумента , а ординаты – соответствующие им значения функции y=f(x).
4) Словесный способ – функция описывается правилом ее составления. Например, функция Дирихле принимает значение 1, если x – рациональное число и 0, если x – иррациональное число.
Выделяют следующие основные свойства функций.
1 Четность и нечетностьФункция y=f(x) называется четной, если для любых значений x из области ее определения выполняется f(–x)=f(x), и нечетной, если f(–x)=–f(x). Если не выполняется ни одно из перечисленных равенств, то y=f(x) называется функцией общего вида. График четной функции симметричен относительно оси Oy, а график нечетной функции симметричен относительно начала координат.
2 МонотонностьФункция y=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Пусть x1,x2ÎX, x2>x1. Тогда функция возрастает на промежутке X, если f(x2)>f(x1), и убывает, если f(x2)f(x1).
Наряду с возрастающими и убывающими функциями рассматривают неубывающие и невозрастающие функции. Функция называется неубывающей (невозрастающей), если при x1,x2ÎX, x2>x1 выполняется неравенство f(x2)≥f(x1) (f(x2)≤f(x1)).
Возрастающие и убывающие функции, а также невозрастающие и неубывающие функции называют монотонными.
3 ОграниченностьФункция y=f(x) называется ограниченной на промежутке X, если существует такое положительное число M>0, что |f(x)|≤M для любого xÎX. В противном случае функция называется неограниченной на X.
4 ПериодичностьФункция y=f(x) называется периодической с периодом T≠0, если для любых x из области определения функции f(x+T)=f(x). В дальнейшем под периодом будем понимать наименьший положительный период функции.
Функция называется явной, если она задана формулой вида y=f(x). Если функция задана уравнением F(x, y)=0, не разрешенным относительно зависимой переменной y, то ее называют неявной.
Пусть y=f(x) есть функция от независимой переменной , определенная на множестве X с областью значений Y. Поставим в соответствие каждому yÎY единственное значение xÎX, при котором f(x)=y.Тогда полученная функция x=φ(y), определенная на множестве Y с областью значений X, называется обратной и обозначается y=f –1 (x). Графики взаимно обратных функций симметричны относительно биссектрисы первой и третьей координатных четвертей .
Пусть функция y=f(u) есть функция переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь является функцией u=φ(x), определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y=f(φ(x)) называется сложной функцией (композицией функций, суперпозицией функций, функцией от функции).
Элементарные функции
К основным элементарным функциям относят:
- степенную функцию y=x n ; y=x – n и y=x 1/ n ;
- показательную функцию y=a x ;
- логарифмическую функцию y=logax;
- тригонометрические функции y=sin x, y=cos x, y=tg x и y=ctg x;
- обратные тригонометрические функции y= arcsin x, y=arccos x, y=arctg x и y=arcctg x.
Из основных элементарных функций новые функции могут быть получены при помощи алгебраических действий и суперпозицией функций.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций суперпозиции, называются элементарными.
Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:
· целая рациональная функция (многочлен или полином)
· дробно-рациональная функция (отношение двух многочленов)
· иррациональная функция (если в составе операций над аргументом имеется извлечение корня).
Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.
Что такое функция в математике
Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.
Разберём пример из жизни. Рассмотрим движение автомобиля. Предположим, что он двигается с постоянной скоростью 60 км/ч .

То, что автомобиль двигается с постоянной скоростью 60 км/ч означает, что автомобиль проезжает 60 км за 1 час .
Зададим себе вопрос: «Сколько километров проедет автомобиль за 2 часа ?».
Очевидно, чтобы найти, сколько километров пройдет автомобиль за 2 часа , нужно 60 умножить на 2 . Мы получим, что за 2 часа автомобиль проедет 120 км .
Составим таблицу, в которой укажем какое расстояние проедет автомобиль за разное время при постоянной скорости 60 км/ч .
| Сколько времени двигается автомобиль | Сколько км проедет автомобиль |
|---|---|
| 1 час | 60 км |
| 2 часа | 120 км |
| 3 часа | 180 км |
Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.
Обозначим за « x » время автомобиля в пути.
Обозначим за « y » расстояние, пройденное автомобилем.
Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).
Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.
Рассчитаем по записанной формуле, сколько пройдет автомобиль за 1 ч . То есть подставим в формулу « y = 60 · x » значение x = 1 .
y = 60 · 1 = 60(км) — пройдёт автомобиль за 1 час . Это совпадает с нашими расчетами ранее.
Теперь рассчитаем для x = 2 .
y = 60 · 2 = 120(км) — пройдёт автомобиль за 2 часа .
Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».
Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:
Запомните!
Функцией называют зависимость « y » от « x ».
- « x » называют переменной или аргументом функции.
- « y » называют зависимой переменной или значением функции.
Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.
Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
Примеры других функций:
- y(x) = 2x
- y(x) = −5x + 2
- y(x) = 12x 2 −1
Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).
Способы задания функции
Существуют три основных способа задания функции. Все способы задания функции в математике тесно связаны друг с другом .
Задание функции формулой
Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента « x » найти значение функции « y ».
Например, рассмотрим функцию, заданную формульным способом.
Найдем значение функции « y » при x = 0 . Для этого подставим в формулу вместо « x »
число « 0 ».
Запишем расчет следующим образом.
Таким же образом найдем значения « y » при x = 1 и при x = 2 .
Найдем значение « y » при x = 1 .
Теперь найдем значение « y » при x = 2 .
Табличный способ задания функции
С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля « y(x) = 60x ».
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений « y » для произвольно выбранных значений « x ».
Найдем значения « y » при x = −1 , x = 0 и x = 1 .

Важно!
Будьте внимательны, когда подставляете значение « x » в функцию,
у которой перед « x » есть минус.
Нельзя терять знак минуса, который стоит перед « x ».
При подстановки отрицательного числа в функцию вместо « x » обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.
Подставим в функцию « y(x) = −x + 4 » вместо « x » отрицательное число « −1 ».
Неправильно

Правильно

Теперь для функции « y(x) = −x + 4 » найдем значения « y » при x = 0 и x = 1 .
Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции « y(x) = −x + 4 ».
| x | y |
|---|---|
| −1 | 5 |
| 4 | |
| 1 | 3 |
Графический способ задания функции
Теперь давайте разберемся, что называют графиком функции и как его построить.
Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.
Рассмотрим функцию « y(x) = −2x + 1 ».
Найдем несколько значений « y » для произвольных « x ». Например, для x = −1 ,
x = 0 и x = 1 .
Результаты запишем в таблицу.
| x | Расчет |
|---|---|
| −1 | y(−1) = −2 · (−1) + 1 = 2 + 1 = 3 |
| y(0) = −2 · 0 + 1 = 0 + 1 = 1 | |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Назовем каждую полученную точку и запишем их координаты в новую таблицу.
| Имя точки | x | y |
|---|---|---|
| (·) A | −1 | 3 |
| (·) B | 1 | |
| (·) C | 1 | −1 |
Отметим точки А(−1;3) , B(0;1) и С(1;−1) на прямоугольной системе координат.

Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции « y(x) = −2x + 1 ».

Запомните!
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо « x ».
Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо « x ».
Полученный график функции « y(x) = −2x + 1 » это бесконечное множество точек, которые лежат на одной прямой.
При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.

Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.
Функция
Отображе́ние или фу́нкция ( лат. functio — «исполнение, осуществление») — одно из основных понятий математики, выражающее зависимость одной величины от другой.
Содержание
Отображение функции.
Наиболее распространенная трактовка понятия функции состоит в его отождествлении с понятием отображения:
Определение. Пусть ” width=”” height=”” /> и ” width=”” height=”” /> — два множества. Закон ” width=”” height=”” />, согласно которому каждому элементу ” width=”” height=”” /> поставлен в соответствие единственный элемент ” width=”” height=”” />, называется отображением множества ” width=”” height=”” /> в множество ” width=”” height=”” /> или функцией, заданной на ” width=”” height=”” /> со значениями в ” width=”” height=”” />.
Отображения обозначают так:
Функции считаются равными, если у них одинаковые области определения и значений и если они определяются одним правилом. Например, все три следующие функции различны:
При необходимости можно различать отображения в зависимости от природы множеств ” width=”” height=”” /> и ” width=”” height=”” />. Если ” width=”” height=”” /> и ” width=”” height=”” /> — числовые множества, такие, как >” width=”” height=”” /> или >” width=”” height=”” />, то отображение называют функцией. Если ” width=”” height=”” /> или ” width=”” height=”” /> многомерны, например, ^>” width=”” height=”” /> или ^>” width=”” height=”” />, то отображение называют ве́ктор-фу́нкцией. Если ” width=”” height=”” /> — произвольной природы, а ” width=”” height=”” /> — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, морфизм и т. д.
Способы задания функции
Словесный
игрек равно целая часть от х. (” width=”” height=”” />)
Аналитический
” width=”” height=”” />
Графический
С помощью графика.
Таблицы
Функция задается таблицей значений. Например:
| X | 1 | 2 | 3 | |
|---|---|---|---|---|
| Y | 1 | 8 | 27 |
Интуитивно можно догадаться, что y = x 3 .
Смежные понятия
Сужение функции.
Пусть дано отображение ” width=”” height=”” />, и ” width=”” height=”” />. Тогда суже́нием функции ” width=”” height=”” /> на ” width=”” height=”” /> называется функция >” width=”” height=”” />, определяемая равенством
(x)=F(x),;forall xin M>” width=”” height=”” />.
Это определение подчеркивает, что фиксация области определения является частью определения функции.
Образ множества
Пусть ” width=”” height=”” />. Тогда о́бразом множества ” width=”” height=”” /> называется подмножество ” width=”” height=”” />, определяемое равенством
>” width=”” height=”” />.
Множество ” width=”” height=”” /> называется образом отображения ” width=”” height=”” />.
Прообраз
Пусть задано отображение ” width=”” height=”” />, ” width=”” height=”” /> и ” width=”” height=”” />. Тогда ” width=”” height=”” /> называется проо́бразом ” width=”” height=”” />, а ” width=”” height=”” /> называется о́бразом ” width=”” height=”” />. Согласно определению отображения, каждый элемент ” width=”” height=”” /> должен иметь ровно один образ, но элемент ” width=”” height=”” /> может не иметь прообразов либо иметь один или несколько.

Пример. Пусть дана функция to mathbb >” width=”” height=”” />, где >” width=”” height=”” />. Тогда
Полный прообраз элемента
Пусть задано отображение ” width=”” height=”” />, и ” width=”” height=”” />. Тогда множество subset X>” width=”” height=”” /> называется по́лным проо́бразом элемента ” width=”” height=”” />. Полный прообраз обозначается (y)>” width=”” height=”” />.

Пример. Пусть to mathbb >” width=”” height=”” />, и ” width=”” height=”” />. Тогда
(1)=left<
Полный прообраз множества
Пусть ” width=”” height=”” />. Тогда проо́бразом множества ” width=”” height=”” /> называется подмножество ” width=”” height=”” />, определяемое равенством
(N)=

Пример. Пусть to mathbb >” width=”” height=”” />, и ” width=”” height=”” />. Тогда
Свойства прообразов и образов
График
Фрагмент графика функции -9x>” width=”” height=”” />
Пусть дано отображение ” width=”” height=”” />. Тогда его гра́фиком ” width=”” height=”” /> называется множество
subset Xtimes Y>” width=”” height=”” />,
где ” width=”” height=”” /> обозначает декартово произведение множеств ” width=”” height=”” /> и ” width=”” height=”” />.
Исторический очерк
Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма «Введение и изучение плоских и телесных мест» ( Р. Декарта ( И. Барроу («Лекции по геометрии», И. Ньютона . Однако термин «функция» впервые появляется лишь в Лопиталя ( И. Бернулли ( Л. Эйлера, данном им во «Введении в анализ бесконечных» ( задачи о колебании струны, предложенное Д. Бернулли ( Д. Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Л.Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»). Эта критика убедительна и с современной точки зрения, ибо не все функции допускают аналитическое изображение (правда, у Д. Бернулли речь идёт о непрерывной функции, которая, как установил в К. Вейерштрасс , всегда аналитически изобразима, но она может и не разлагаться в тригонометрический ряд). Однако другие аргументы Л.Эйлера уже ошибочны. Например, он считал, что разложение функции в тригонометрический ряд доставляет для неё единое аналитическое выражение, в то время как она может быть «смешанной» функцией, представимой на разных отрезках разными формулами. На самом деле одно другому не противоречит, но в ту эпоху казалось невозможным, чтобы два аналитических выражения, совпадая на части отрезка, не совпадали на всём его протяжении..
С начала обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям ” width=”” height=”” />, содержащимся между ” width=”” height=”” /> и какой-либо величиной ” width=”” height=”” />». Близко к современному и определение называть число, которое даётся для каждого ” width=”” height=”” /> и вместе с ” width=”” height=”” /> постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной». Там же немного ниже сказано: «Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе». Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Примечания
См. также
Различные классы функций:
- Ильин В. А., Позняк Э. Г. Основы математического анализа, ч.1, 3 изд., М., 1971;. ч.2, 2 изд., М., 1980;
- Кудрявцев Л. Д., Математический анализ, 2 изд., т.1-2, 1973,
- Никольский С. М., Курс математического анализа, 2 изд., т.1-2, М., 1975;
- История математики, т.2-3, М., 1970-72.
- Функция. Математический энциклопедический словарь. Гл. ред. Ю. В. Прохоров. М.: «Большая российская энциклопедия». 1995.
Эта статья содержит материал из статьи Функция русской Википедии.
Определение, понятие, свойства и значение функций в алгебре
Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости – первые две формулы, для трехмерной системы координат – все три формулы) вычисляются по формулам:

Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):
График квадратичной функции (Парабола)
График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p – на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q – на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

Графики других функций
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота – это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:

Графики периодических (тригонометрических) функций
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:

Большинство примеров периодических функций – это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.


Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Определение функции
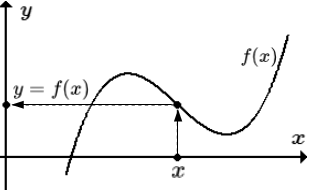
Определение функции, области задания и множества значений. Определения, связанные с обозначением функции. Определения сложной, числовой, действительной, монотонной и многозначной функции. Определения максимума, минимума, верхней и нижней граней для ограниченных функций. Сужение и продолжение функций.
Определение функции
Функцией y = f ( x ) называется закон (правило, отображение), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y . Область определения функции Множество X называется областью определения функции. Область определения иногда называют
множеством определения или множеством задания функции. Множество значений функции Множество элементов y ∈ Y , которые имеют прообразы во множестве X , называется множеством значений функции, или областью значений. Аргумент функции Элемент x ∈ X называют аргументом функции или независимой переменной. Значение функции Элемент y ∈ Y называют значением функции или зависимой переменной. Характеристика функции Само отображение f называется характеристикой функции.
Характеристика f обладает тем свойством, что если два элемента и из множества определения имеют равные значения: , то .
Символ, обозначающий характеристику, может совпадать с символом элемента значения функции. То есть можно записать так: . При этом стоит помнить, что y – это элемент из множества значений функции, а – это правило, по которому для элемента x ставится в соответствие элемент y .
Сам процесс вычисления функции состоит из трех шагов. На первом шаге мы выбираем элемент x из множества X . Далее, с помощью правила , элементу x ставится в соответствие элемент множества Y . На третьем шаге этот элемент присваивается переменной y .
Частным значением функции называют значение функции при выбранном (частном) значении ее аргумента.
Графиком функции f называется множество пар .
Сложные функции
Сложная функция Пусть заданы функции и . Причем область определения функции f содержит множество значений функции g . Тогда каждому элементу t из области определения функции g соответствует элемент x , а этому x соответствует y . Такое соответствие называют сложной функцией: . Сложную функцию также называют
композицией или суперпозицией функций и иногда обозначают так: .
В математическом анализе принято считать, что если характеристика функции обозначена одной буквой или символом, то она задает одно и то же соответствие. Однако, в других дисциплинах, встречается и другой способ обозначений, согласно которому отображения с одной характеристикой, но разными аргументами, считаются различными. То есть отображения и считаются различными. Приведем пример из физики. Допустим мы рассматриваем зависимость импульса от координаты . И пусть мы имеем зависимость координаты от времени . Тогда зависимость импульса от времени является сложной функцией . Но ее, для краткости, обозначают так: . При таком подходе и – это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например . Тогда явно видно, что и – это разные функции.
Действительные функции
Область определения функции и множество ее значений могут быть любыми множествами.
Например, числовые последовательности – это функции, областью определения которых является множество натуральных чисел, а множеством значений – вещественные или комплексные числа.
Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора . Здесь областью определения является множество всех возможных пар векторов . Множеством значений является множество всех векторов.
Логическое выражение является функцией. Ее область определения – это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов – “истина” и “ложь”.
В математическом анализе большую роль играют числовые функции.
Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
Ограниченная сверху (снизу) функция Действительная функция называется ограниченной сверху (снизу), если существует такое число M , что для всех выполняется неравенство:
. Ограниченная функция Числовая функция называется ограниченной, если существует такое число M , что для всех :
.
Максимумом M (минимумом m ) функции f , на некотором множестве X , называют значение функции при некотором значении ее аргумента , при котором для всех ,
.
Верхняя и нижняя грани
Верхняя грань (точная верхняя граница) функции Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s , для которого:
1) для всех ;
2) для любого , найдется такой аргумент , значение функции от которого превосходит s′ : .
Верхняя грань функции может обозначаться так:
.
Верхней гранью неограниченной сверху функции является бесконечно удаленная точка . Нижняя грань (точная нижняя граница) функции Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i , для которого:
1) для всех ;
2) для любого , найдется такой аргумент , значение функции от которого меньше чем i′ : .
Нижняя грань функции может обозначаться так:
.
Нижней гранью неограниченной снизу функции является бесконечно удаленная точка .
Таким образом, любая действительная функция, на не пустом множестве X , имеет верхнюю и нижнюю грани. Но не всякая функция имеет максимум и минимум.
В качестве примера рассмотрим функцию , заданную на открытом интервале .
Она ограничена, на этом интервале, сверху значением 1 и снизу – значением 0 :
для всех .
Эта функция имеет верхнюю и нижнюю грани:
.
Но она не имеет максимума и минимума.
Если мы рассмотрим туже функцию на отрезке , то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум:
для всех ;
;
.
Монотонные функции
Возрастающая (убывающая) функция Пусть функция определена на некотором множестве действительных чисел X . Функция называется строго возрастающей (строго убывающей), если для всех таких что выполняется неравенство:
.
Функция называется неубывающей (невозрастающей), если для всех таких что выполняется неравенство:
. Монотонная функция Функция называется монотонной, если она неубывающая или невозрастающая.
Многозначные функции
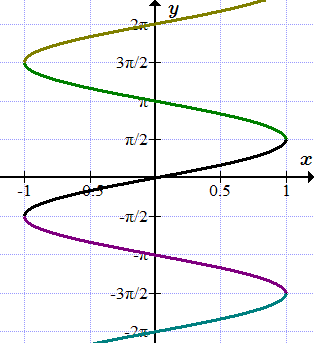
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
В качестве примера рассмотрим функцию арксинус: . Она является обратной к функции синус и определяется из уравнения:
(1) .
При заданном значении независимой переменной x , принадлежащему интервалу , этому уравнению удовлетворяет бесконечно много значений y (см. рисунок).
Наложим на решения уравнения (1) ограничение. Пусть
(2) .
При таком условии, заданному значению , соответствует только одно решение уравнения (1). То есть соответствие, определяемое уравнением (1) при условии (2) является функцией.
Вместо условия (2) можно наложить любое другое условие вида:
(2.n) ,
где n – целое. В результате, для каждого значения n , мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией. А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функции.
Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.
Сужение и продолжение функции
Выше мы указали, что если область определения функции синус, , сузить до отрезка , то полученная в результате новая функция будет строго монотонной на этом отрезке и иметь обратную функцию. Такая операция называется сужением функции. В результате ее применения получается новая функция, которая в данном примере обозначается так: .
Сужение функции Пусть функция определена на множестве X . И пусть множество M является его подмножеством: . Определим функцию так, чтобы ее областью определения было множество M . И пусть на этом множестве она принимает те же значения, что и функция :
.
Тогда функция называется сужением функции f на множество M . Сужение функции обозначают так:
, или . Продолжение функции Пусть функция определена на множестве X , а функция – на множестве M , которое является подмножеством X : . И пусть функция является сужением функции на множество M . Тогда функция называется продолжением функции g на множество X .
Выполнить операцию сужения функции на заданное множество можно только одним способом. А вот выполнить продолжение можно бесконечным числом способов. Особую роль продолжение играет в теории функций комплексного переменного. Там показывается, что если функция является аналитической (то есть имеет производную) на некотором множестве M , то существует только единственное ее аналитическое продолжение на множество X .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.





