Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Урок 22. Измерение отрезков

Длина отрезка – число, которое показывает, сколько раз в отрезке содержится единичный отрезок.

Единичный отрезок – это отрезок, длина которого принята за единицу измерения.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.

Теоретический материал для самостоятельного изучения

Каждому человеку неоднократно приходилось что-то измерять: свой рост, длину прыжка, высоту потолка и многое другое. Все эти действия означают вычисление величины какого-нибудь отрезка. Каким же образом можно измерить длину отрезка? На этот вопрос ответим в ходе урока.

За свою историю человечество придумало много разных единиц длины. Позже появились меры, заимствованные из природы:

– пядь – расстояние между растянутыми большим и указательным пальцами;

– вершок – длина основной фаланги указательного пальца;

– локоть – расстояние от локтевого сустава до конца вытянутого среднего пальца руки.

Некоторые названия сохранились до сих пор: ярд, фут, пядь, дюйм.

Ну, а герои одного известного мультфильма измеряли длину удава в попугаях. В зависимости от того, в ком измеряли удава, он становился то длиннее, то короче.

Два слонёнка, пять мартышек или тридцать восемь попугаев.

«А в попугаях я гораздо длиннее!» – воскликнул удав.

На самом деле мы с вами понимаем, что его размеры не менялись. Тогда возникает вопрос: в чём измерять? Что брать за единицу длины? Слонёнка, попугая или мартышку.

Измерить длину какого-нибудь отрезка в заданных единицах измерения – значит найти число, показывающее, сколько единичных отрезков поместится в данном отрезке.

Длиной отрезка называют число, которое показывает, сколько раз в отрезке содержится единица измерения.

Отрезок, длина которого принята за единицу измерения, называется единичным отрезком.

Чем же можно измерить длину отрезка?

Наиболее древними геометрическими инструментами являются линейка и циркуль, последний был изобретён в первом веке в Древней Греции.

Для более точных измерений используют миллиметровую линейку и штангенциркуль.

Если при измерении линейкой определённого отрезка какая-то точка не совпадает с делением шкалы, то можно говорить о приближенном значении длины этого отрезка. Приближенное значение длины может быть с избытком, с недостатком и с округлением. Например, на рисунке отрезок АВ может быть измерен с точностью до сантиметров. Его длину можно найти приближенно с избытком или с недостатком. В таких случаях говорят, что с недостатком его длина равна 5 см, а с избытком – 6 см. Это записывают так: АВ 5 см (с недостатком); АВ 6 см (с избытком).

Далее построим отрезок ВК заданной длины –например, 8см. Для этого отметим точку В и приложим к ней линейку, совместив точку В с нулём. Затем отмеряем с помощью линейки 8 см, отмечаем точку К и соединяем обе точки линией.

Такой отрезок можно построить и с помощью циркуля. Для этого отметим точку В. Приложим к линейке циркуль, выставив его ножки на восемь сантиметров. Перенесём циркуль к точке В, поместив на неё одну ножку, а другой ножкой поставим точку К. Соединив обе точки линией, получим отрезок с длиной 8 см.

Отрезки можно сравнить с помощью измерителя –например, циркуля. Для этого попеременно подставляем ножки циркуля ко всем предложенным для сравнения отрезкам. При этом они должны быть выставлены по одному из отрезков. Если длины отрезков одинаковы, то отрезки считают равными и пишут CD = КМ.

Если один из отрезков является частью другого, следовательно, он короче. Например, ЕН короче EF, так как отрезок EH является частью EF.

Рассмотрим ещё одно свойство длин.

Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ. Пишут: АВ = АС + СВ.

Наши органы чувств – это один из способов получения информации об окружающем нас мире, но информация полученная таким образом, бывает искажена.

Посмотрите на рисунки и ответьте на вопрос, равны ли отрезки?

На первый взгляд покажется, что правый отрезок больше, чем левый, но при сравнении с помощью линейки окажется, что отрезки равны.

Такая же ситуация, складывается и со следующей картинкой. Кажется, что нижний отрезок больше, чем верхний, но при наложении линейки окажется, что отрезки равны.

В другом же случае на тот же вопрос о равенстве отрезков ответ очевиден.

Таким образом, можно сделать вывод, что глазомерные оценки геометрических реальных величин неточны.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка.

Сравните длины горизонтального и вертикального отрезков?

1. Отрезки равны
2. Вертикальный отрезок больше
3. Горизонтальный отрезок больше

Правильный ответ: при выполнении данного задания нужно использовать линейку, нужно измерить длину каждого отрезка и сравнить их. В результате измерений мы увидим, что отрезки равны.

№2. Тип задания: выделение цветом.

Точка К расположена на прямой между точками А и В. Длина отрезка АК = 8 см, длина отрезка КВ на 2 см больше длины отрезка АК. Какова длина отрезка АВ?

Отрезок

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

Свойства длин отрезков:

Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB < CA.

Если точки A и B совпадут, то отрезки CA и CB равны:

CA = CB.

Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.

При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.

Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то

AB > AC.

Так как отрезки AB и AC имеют одинаковую длину, то

AB = AC.

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Как сравнить длины отрезков?

Сравнить 2 отрезка на плоскости — это типичная задача по геометрии для учеников 7 класса. Существует несколько разных методов выполнения данного сравнения, и мы подробно расскажем о каждом из них.

Подобного рода задачи выполняются элементарно и являются основой для изучения дальнейшего материала. Стоит один раз запомнить этот несложный процесс, и в дальнейшем уже не возникнет никаких трудностей с аналогичными заданиями.

Метод наложения

Одной из простейших геометрических фигур является отрезок . Для того чтобы сравнивать отрезки, можно использовать два способа:

1. Метод наложения.
2. Измерение длин.

Пусть нам даны два отрезка AB и СD:

Совместим начало отрезка AB и СD (точки A и С).

Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

MK = KV, K — середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок STтак, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ < PO (т.к. 3 < 5), QL = PO (т.к. 5 = 5).

• Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
• Если при измерении отрезков их длины равны, то отрезки равны.

Как сравнить 2 отрезка: способы решения задачи

Что такое отрезок

Прежде чем рассказать, как сравнить 2 отрезка, давайте разберем, что такое отрезок на плоскости.

Определение из учебника по геометрии гласит, что отрезок — это часть прямой, которая с двух сторон ограничивается двумя точками.

Если рассматривать одну прямую, отрезком будет считаться множество, которое состоит из двух разных точек этой прямой (собственно, концов отрезка), а также остального множества из всех точек, которые располагаются между ними (так называемых внутренних точек).

Сравнение двух отрезков

Итак, в вопросе о том, как сравнить 2 отрезка, можно выделить следующие методы:

• Наложение. Для того чтобы выполнить сравнение двух отрезков, нужно выполнить наложение одного из них на другой. Соответственно, тот отрезок, который будет содержать внутри себя второй отрезок целиком, больше. Если концы этих отрезков совпали — значит, их длины равны.
• Второй способ, как сравнить 2 отрезка в геометрии — это выяснить, на какое количество единиц отличается их длина. Для этого нужно при помощи линейки с одинаковыми значениями провести измерение сначала одного отрезка, затем другого, и из первого результата вычесть второй.

В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.

Вывод

Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.

Прямая и отрезок, измерение и сравнение отрезков

Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.

Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины.

Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.

Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках.

Понятия прямой и точки связаны тремя аксиомами геометрии:

• Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
• Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
• Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.

Для двух прямых актуально их взаимное расположение. Возможны три случая:

1. Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
2. Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
3. Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.

В этой статье мы не будем подробно останавливаться на этих понятиях.

Отрезок

Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками. Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.

Отрезки будем обозначать двумя её точками концов в квадратных скобках.

Сравнение отрезков

Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.

Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.

Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:

1. Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу.
2. Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

• визуальный способ;
• измерительный;
• сравнение наложением;
• сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

• Способы сравнения двух отрезков
• Измерение длины
• Наложение друг на друга
• Сравнение в координатной сетке
• Примеры

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (&gt,, &lt,, =). Например, длина отрезка АБ — 2 см, а ВГ — 8 см, записываем результат сравнения так: АБ &lt, ВГ или ВГ &gt, АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

• визуальный способ,
• измерительный,
• сравнение наложением,
• сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

• Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
• Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (&gt, или &lt,).

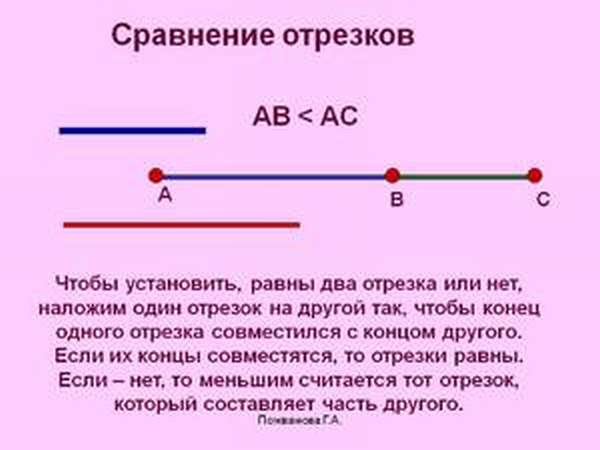
Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.

Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.

Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.

Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.

Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1, Х2, Y2) и b (Х3, Y3, X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

• Длина, а — Da = √((X1 — X2) ² + (Y1 — Y2) ²),
• Длина b — Db = √((X3 — X4) ² + (Y3 — Y4) ²).

Пусть X1 = -7, Y1 = 4, X2 = 3, Y2 = -4, X3 = -3, Y3 = -5, X4 = 0, Y4 = -3. Получаем:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 &gt, √ 73, значит, Da &gt, Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Читайте также: Моря, омывающие Атлантический океан: характеристика водоема, список морей, история формирования и флора и фауна

Примеры

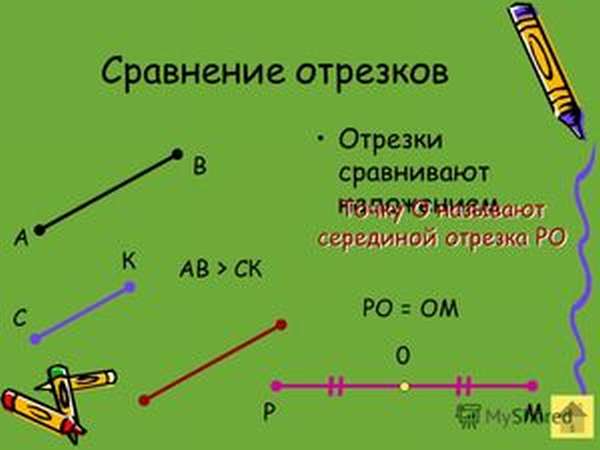
Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ&lt, ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.

Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8&gt,2, значит, CD&gt,AB, то есть отрезок CD длиннее AB.

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

• визуальный способ;
• измерительный;
• сравнение наложением;
• сравнение в координатной сетке.

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

• Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
• Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> или <).

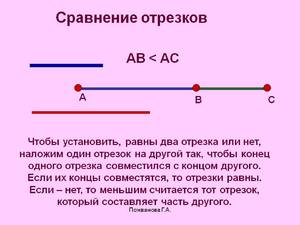
Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.

Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.

Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.

Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.

Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

• Длина, а — Da = √((X1 — X2) ² + (Y1 — Y2) ²);
• Длина b — Db = √((X3 — X4) ² + (Y3 — Y4) ²).

Пусть X1 = -7, Y1 = 4, X2 = 3, Y2 = -4, X3 = -3, Y3 = -5, X4 = 0, Y4 = -3. Получаем:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 > √ 73, значит, Da > Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

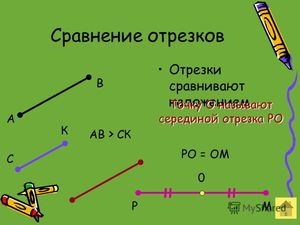
Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ< ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.

Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8>2, значит, CD>AB, то есть отрезок CD длиннее AB.

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Слово геометрия древнегреческого происхождения, оно означает «землемерие» («гео» – земля, «метрео» – измерять).

Геометрия – древняя наука, возникла в результате практической деятельности человека: строительства зданий и дорог, установления земельных наделов и определения их размеров.

Становление данной науки происходило тысячелетиями.

В настоящее время геометрия – наука, занимающаяся изучением геометрических фигур, их свойствами, размерами и преобразованиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

Точка – это неделимая фигура, не имеет частей и размеров (высоты, радиуса, длины и т.д.), направления и других характеристик.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Отрезок – это часть прямой линии, ограниченной двумя точками.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

А и В – концы отрезка.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок АВ и ВА – это один и тот же отрезок.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Длина в геометрии – это величина, которая характеризует протяженность.

Длина отрезка – это расстояние между концами отрезка.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

2. Совмещение отрезков – более точный способ сравнения отрезков.

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

1. Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
2. Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
3. Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

A и E – концы ломаной.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника – это сумма длин всех сторон.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник – 6 углов и 6 сторон.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник – плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

А, В, С – вершины треугольника АBC.

Отрезки AB, BC, АC– стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.