Как правильно разложить квадратный трёхчлен, формулы разложения множителей, уравнения и примеры

Разложение многочлена на множители

Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.

Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.

Теория

Когда любой многочлен со степенью n , имеющие вид P n x = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 , представляют в виде произведения с постоянным множителем со старшей степенью a n и n линейных множителей ( x – x i ) , i = 1 , 2 , … , n , тогда P n ( x ) = a n ( x – x n ) ( x – x n – 1 ) · . . . · ( x – x 1 ) , где x i , i = 1 , 2 , … , n – это и есть корни многочлена.

Теорема предназначена для корней комплексного типа x i , i = 1 , 2 , … , n и для комплексных коэффициентов a k , k = 0 , 1 , 2 , … , n . Это и есть основа любого разложения.

Когда коэффициенты вида a k , k = 0 , 1 , 2 , … , n являются действительными числами, тогда комплексные корни, которые будут встречаться сопряженными парами. Например, корни x 1 и x 2 , относящиеся к многочлену вида P n x = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид P n ( x ) = a n ( x – x n ) ( x – x n – 1 ) · . . . · ( x – x 3 ) x 2 + p x + q , где x 2 + p x + q = ( x – x 1 ) ( x – x 2 ) .

Замечание

Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.

Основная теорема алгебры

Любой многочлен со степенью n имеет как минимум один корень.

Теорема Безу

После того, как произвели деление многочлена вида P n x = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 на ( x – s ) , тогда получаем остаток, который равен многочлену в точке s , тогда получим

P n x = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 = ( x – s ) · Q n – 1 ( x ) + P n ( s ) , где Q n – 1 ( x ) является многочленом со степенью n – 1 .

Следствие из теоремы Безу

Когда корень многочлена P n ( x ) считается s , тогда P n x = a n x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 = ( x – s ) · Q n – 1 ( x ) . Данное следствие является достаточным при употреблении для описания решения.

Разложение на множители квадратного трехчлена

Квадратный трехчлен вида a x 2 + b x + c можно разложить на линейные множители. тогда получим, что a x 2 + b x + c = a ( x – x 1 ) ( x – x 2 ) , где x 1 и x 2 – это корни (комплексные или действительные).

Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.

Произвести разложение квадратного трехчлена на множители.

Необходимо найти корни уравнения 4 x 2 – 5 x + 1 = 0 . Для этого необходимо найти значение дискриминанта по формуле, тогда получим D = ( – 5 ) 2 – 4 · 4 · 1 = 9 . Отсюда имеем, что

x 1 = 5 – 9 2 · 4 = 1 4 x 2 = 5 + 9 2 · 4 = 1

Отсюда получаем, что 4 x 2 – 5 x + 1 = 4 x – 1 4 x – 1 .

Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:

4 x – 1 4 x – 1 = 4 x 2 – x – 1 4 x + 1 4 = 4 x 2 – 5 x + 1

После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.

Произвести разложение на множители квадратный трехчлен вида 3 x 2 – 7 x – 11 .

Получим, что необходимо вычислить получившееся квадратное уравнение вида 3 x 2 – 7 x – 11 = 0 .

Чтобы найти корни, надо определить значение дискриминанта. Получим, что

3 x 2 – 7 x – 11 = 0 D = ( – 7 ) 2 – 4 · 3 · ( – 11 ) = 181 x 1 = 7 + D 2 · 3 = 7 + 181 6 x 2 = 7 – D 2 · 3 = 7 – 181 6

Отсюда получаем, что 3 x 2 – 7 x – 11 = 3 x – 7 + 181 6 x – 7 – 181 6 .

Произвести разложение многочлена 2 x 2 + 1 на множители.

Теперь нужно решить квадратное уравнение 2 x 2 + 1 = 0 и найти его корни. Получим, что

2 x 2 + 1 = 0 x 2 = – 1 2 x 1 = – 1 2 = 1 2 · i x 2 = – 1 2 = – 1 2 · i

Эти корни называют комплексно сопряженными, значит само разложение можно изобразить как 2 x 2 + 1 = 2 x – 1 2 · i x + 1 2 · i .

Произвести разложение квадратного трехчлена x 2 + 1 3 x + 1 .

Для начала необходимо решить квадратное уравнение вида x 2 + 1 3 x + 1 = 0 и найти его корни.

x 2 + 1 3 x + 1 = 0 D = 1 3 2 – 4 · 1 · 1 = – 35 9 x 1 = – 1 3 + D 2 · 1 = – 1 3 + 35 3 · i 2 = – 1 + 35 · i 6 = – 1 6 + 35 6 · i x 2 = – 1 3 – D 2 · 1 = – 1 3 – 35 3 · i 2 = – 1 – 35 · i 6 = – 1 6 – 35 6 · i

Получив корни, запишем

x 2 + 1 3 x + 1 = x – – 1 6 + 35 6 · i x – – 1 6 – 35 6 · i = = x + 1 6 – 35 6 · i x + 1 6 + 35 6 · i

Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.

Способы разложения на множители многочлена степени выше второй

При разложении предполагается универсальный метод. Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x 1 и понизить его степень при помощи деления на многочлена на 1 делением на ( x – x 1 ) . Полученный многочлен нуждается в нахождении корня x 2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.

Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.

Вынесение общего множителя за скобки

Рассмотрим случай, когда свободный член равняется нулю, тогда вид многочлена становится как P n ( x ) = a n x n + a n – 1 x n – 1 + . . . + a 1 x .

Видно, что корень такого многочлена будет равняться x 1 = 0 , тогда можно представить многочлен в виде выражения P n ( x ) = a n x n + a n – 1 x n – 1 + . . . + a 1 x = = x ( a n x n – 1 + a n – 1 x n – 2 + . . . + a 1 )

Данный способ считается вынесением общего множителя за скобки.

Выполнить разложение многочлена третьей степени 4 x 3 + 8 x 2 – x на множители.

Видим, что x 1 = 0 – это корень заданного многочлена, тогда можно произвести вынесение х за скобки всего выражения. Получаем:

4 x 3 + 8 x 2 – x = x ( 4 x 2 + 8 x – 1 )

Переходим к нахождению корней квадратного трехчлена 4 x 2 + 8 x – 1 . Найдем дискриминант и корни:

D = 8 2 – 4 · 4 · ( – 1 ) = 80 x 1 = – 8 + D 2 · 4 = – 1 + 5 2 x 2 = – 8 – D 2 · 4 = – 1 – 5 2

Тогда следует, что

4 x 3 + 8 x 2 – x = x 4 x 2 + 8 x – 1 = = 4 x x – – 1 + 5 2 x – – 1 – 5 2 = = 4 x x + 1 – 5 2 x + 1 + 5 2

Разложение на множители многочлена с рациональными корнями

Для начала примем за рассмотрение способ разложения, содержащий целые коэффициенты вида P n ( x ) = x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 , где коэффициента при старшей степени равняется 1 .

Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.

Произвести разложение выражения f ( x ) = x 4 + 3 x 3 – x 2 – 9 x – 18 .

Рассмотрим, имеются ли целые корни. Необходимо выписать делители числа – 18 . Получим, что ± 1 , ± 2 , ± 3 , ± 6 , ± 9 , ± 18 . Отсюда следует, что данный многочлен имеет целые корни. Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:

x i	Коэффициенты многочленов
1	3	– 1	– 9	– 18
1	1	3 + 1 · 1 = 4	– 1 + 4 · 1 = 3	– 9 + 3 · 1 = – 6	– 18 + ( – 6 ) · 1 = – 24
– 1	1	3 + 1 · ( – 1 ) = 2	– 1 + 2 · ( – 1 ) = – 3	– 9 + ( – 3 ) · ( – 1 ) = – 6	– 18 + ( – 6 ) · ( – 1 ) = – 12
2	1	3 + 1 · 2 = 5	– 1 + 5 · 2 = 9	– 9 + 9 · 2 = 9	– 18 + 9 · 2 = 0
2	1	5 + 1 · 2 = 7	9 + 7 · 2 = 23	9 + 23 · 2 = 55
– 2	1	5 + 1 · ( – 2 ) = 3	9 + 3 · ( – 2 ) = 3	9 + 3 · ( – 2 ) = 3
3	1	5 + 1 · 3 = 8	9 + 8 · 3 = 33	9 + 33 · 3 = 108
– 3	1	5 + 1 · ( – 3 ) = 2	9 + 2 · ( – 3 ) = 3	9 + 3 · ( – 3 ) = 0

Отсюда следует, что х = 2 и х = – 3 – это корни исходного многочлена, который можно представить как произведение вида:

f ( x ) = x 4 + 3 x 3 – x 2 – 9 x – 18 = ( x – 2 ) ( x 3 + 5 x 2 + 9 x + 9 ) = = ( x – 2 ) ( x + 3 ) ( x 2 + 2 x + 3 )

Переходим к разложению квадратного трехчлена вида x 2 + 2 x + 3 .

Так как дискриминант получаем отрицательный, значит, действительных корней нет.

Ответ: f ( x ) = x 4 + 3 x 3 – x 2 – 9 x – 18 = ( x – 2 ) ( x + 3 ) ( x 2 + 2 x + 3 )

Допускается использование подбором корня и деление многочлена на многочлен вместо схемы Горнера. Перейдем к рассмотрению разложения многочлена, содержащим целые коэффициенты вида P n ( x ) = x n + a n – 1 x n – 1 + . . . + a 1 x + a 0 , старший из которых на равняется единице.

Этот случай имеет место быть для дробно-рациональных дробей.

Произвести разложение на множители f ( x ) = 2 x 3 + 19 x 2 + 41 x + 15 .

Необходимо выполнить замену переменной y = 2 x , следует переходить к многочлену с коэффициентами равными 1 при старшей степени. Необходимо начать с умножения выражения на 4 . Получаем, что

4 f ( x ) = 2 3 · x 3 + 19 · 2 2 · x 2 + 82 · 2 · x + 60 = = y 3 + 19 y 2 + 82 y + 60 = g ( y )

Когда получившаяся функция вида g ( y ) = y 3 + 19 y 2 + 82 y + 60 имеет целые корни, тогда их нахождение среди делителей свободного члена. Запись примет вид:

± 1 , ± 2 , ± 3 , ± 4 , ± 5 , ± 6 , ± 10 , ± 12 , ± 15 , ± 20 , ± 30 , ± 60

Перейдем к вычислению функции g ( y ) в этих точка для того, чтобы получить в результате ноль. Получаем, что

g ( 1 ) = 1 3 + 19 · 1 2 + 82 · 1 + 60 = 162 g ( – 1 ) = ( – 1 ) 3 + 19 · ( – 1 ) 2 + 82 · ( – 1 ) + 60 = – 4 g ( 2 ) = 2 3 + 19 · 2 2 + 82 · 2 + 60 = 308 g ( – 2 ) = ( – 2 ) 3 + 19 · ( – 2 ) 2 + 82 · ( – 2 ) + 60 = – 36 g ( 3 ) = 3 3 + 19 · 3 2 + 82 · 3 + 60 = 504 g ( – 3 ) = ( – 3 ) 3 + 19 · ( – 3 ) 2 + 82 · ( – 3 ) + 60 = – 42 g ( 4 ) = 4 3 + 19 · 4 2 + 82 · 4 + 60 = 756 g ( – 4 ) = ( – 4 ) 3 + 19 · ( – 4 ) 2 + 82 · ( – 4 ) + 60 = – 28 g ( 5 ) = 5 3 + 19 · 5 2 + 82 · 5 + 60 = 1070 g ( – 5 ) = ( – 5 ) 3 + 19 · ( – 5 ) 2 + 82 · ( – 5 ) + 60

Получаем, что у = – 5 – это корень уравнения вида y 3 + 19 y 2 + 82 y + 60 , значит, x = y 2 = – 5 2 – это корень исходной функции.

Необходимо произвести деление столбиком 2 x 3 + 19 x 2 + 41 x + 15 на x + 5 2 .

Решение

Запишем и получим:

2 x 3 + 19 x 2 + 41 x + 15 = x + 5 2 ( 2 x 2 + 14 x + 6 ) = = 2 x + 5 2 ( x 2 + 7 x + 3 )

Проверка делителей займет много времени, поэтому выгодней предпринять разложение на множители полученного квадратного трехчлена вида x 2 + 7 x + 3 . Приравниванием к нулю и находим дискриминант.

x 2 + 7 x + 3 = 0 D = 7 2 – 4 · 1 · 3 = 37 x 1 = – 7 + 37 2 x 2 = – 7 – 37 2 ⇒ x 2 + 7 x + 3 = x + 7 2 – 37 2 x + 7 2 + 37 2

Отсюда следует, что

2 x 3 + 19 x 2 + 41 x + 15 = 2 x + 5 2 x 2 + 7 x + 3 = = 2 x + 5 2 x + 7 2 – 37 2 x + 7 2 + 37 2

Искусственные приемы при разложении многочлена на множители

Рациональные корни не присущи всем многочленам. Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.

Способ группировки

Бывают случаи, когда можно сгруппировывать слагаемые многочлена для нахождения общего множителя и вынесения его за скобки.

Произвести разложение многочлена x 4 + 4 x 3 – x 2 – 8 x – 2 на множители.

Потому как коэффициенты – целые числа, тогда корни предположительно тоже могут быть целыми. Для проверки возьмем значения 1 , – 1 , 2 и – 2 для того, чтобы вычислить значение многочлена в этих точках. Получаем, что

1 4 + 4 · 1 3 – 1 2 – 8 · 1 – 2 = – 6 ≠ 0 ( – 1 ) 4 + 4 · ( – 1 ) 3 – ( – 1 ) 2 – 8 · ( – 1 ) – 2 = 2 ≠ 0 2 4 + 4 · 2 3 – 2 2 – 8 · 2 – 2 = 26 ≠ 0 ( – 2 ) 4 + 4 · ( – 2 ) 3 – ( – 2 ) 2 – 8 · ( – 2 ) – 2 = – 6 ≠ 0

Отсюда видно, что корней нет, необходимо использовать другой способ разложения и решения.

Необходимо провести группировку:

x 4 + 4 x 3 – x 2 – 8 x – 2 = x 4 + 4 x 3 – 2 x 2 + x 2 – 8 x – 2 = = ( x 4 – 2 x 2 ) + ( 4 x 3 – 8 x ) + x 2 – 2 = = x 2 ( x 2 – 2 ) + 4 x ( x 2 – 2 ) + x 2 – 2 = = ( x 2 – 2 ) ( x 2 + 4 x + 1 )

После группировки исходного многочлена необходимо представить его как произведение двух квадратных трехчленов. Для этого нам понадобится произвести разложение на множители. получаем, что

x 2 – 2 = 0 x 2 = 2 x 1 = 2 x 2 = – 2 ⇒ x 2 – 2 = x – 2 x + 2 x 2 + 4 x + 1 = 0 D = 4 2 – 4 · 1 · 1 = 12 x 1 = – 4 – D 2 · 1 = – 2 – 3 x 2 = – 4 – D 2 · 1 = – 2 – 3 ⇒ x 2 + 4 x + 1 = x + 2 – 3 x + 2 + 3

x 4 + 4 x 3 – x 2 – 8 x – 2 = x 2 – 2 x 2 + 4 x + 1 = = x – 2 x + 2 x + 2 – 3 x + 2 + 3

Простота группировки не говорит о том, что выбрать слагаемы достаточно легко. Определенного способа решения не существует, поэтому необходимо пользоваться специальными теоремами и правилами.

Произвести разложение на множители многочлен x 4 + 3 x 3 – x 2 – 4 x + 2 .

Заданный многочлен не имеет целых корней. Следует произвести группировку слагаемых. Получаем, что

x 4 + 3 x 3 – x 2 – 4 x + 2 = = ( x 4 + x 3 ) + ( 2 x 3 + 2 x 2 ) + ( – 2 x 2 – 2 x ) – x 2 – 2 x + 2 = = x 2 ( x 2 + x ) + 2 x ( x 2 + x ) – 2 ( x 2 + x ) – ( x 2 + 2 x – 2 ) = = ( x 2 + x ) ( x 2 + 2 x – 2 ) – ( x 2 + 2 x – 2 ) = ( x 2 + x – 1 ) ( x 2 + 2 x – 2 )

После разложения на множители получим, что

x 4 + 3 x 3 – x 2 – 4 x + 2 = x 2 + x – 1 x 2 + 2 x – 2 = = x + 1 + 3 x + 1 – 3 x + 1 2 + 5 2 x + 1 2 – 5 2

Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители

Внешний вид зачастую не всегда дает понять, каким способом необходимо воспользоваться при разложении. После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.

Произвести разложение многочлена x 4 + 4 x 3 + 6 x 2 + 4 x – 2 на множители.

Необходимо выполнить преобразование выражения к виду

x 4 + 4 x 3 + 6 x 2 + 4 x – 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 – 3

На последовательность коэффициентов суммы в скобках указывает выражение x + 1 4 .

Значит, имеем x 4 + 4 x 3 + 6 x 2 + 4 x – 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 – 3 = x + 1 4 – 3 .

После применения разности квадратов, получим

x 4 + 4 x 3 + 6 x 2 + 4 x – 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 – 3 = x + 1 4 – 3 = = x + 1 4 – 3 = x + 1 2 – 3 x + 1 2 + 3

Рассмотрим выражение, которое находится во второй скобке. Понятно, что там коней нет, поэтому следует применить формулу разности квадратов еще раз. Получаем выражение вида

x 4 + 4 x 3 + 6 x 2 + 4 x – 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 – 3 = x + 1 4 – 3 = = x + 1 4 – 3 = x + 1 2 – 3 x + 1 2 + 3 = = x + 1 – 3 4 x + 1 + 3 4 x 2 + 2 x + 1 + 3

Произвести разложение на множители x 3 + 6 x 2 + 12 x + 6 .

Займемся преобразованием выражения. Получаем, что

x 3 + 6 x 2 + 12 x + 6 = x 3 + 3 · 2 · x 2 + 3 · 2 2 · x + 2 3 – 2 = ( x + 2 ) 3 – 2

Необходимо применить формулу сокращенного умножения разности кубов. Получаем:

x 3 + 6 x 2 + 12 x + 6 = = ( x + 2 ) 3 – 2 = = x + 2 – 2 3 x + 2 2 + 2 3 x + 2 + 4 3 = = x + 2 – 2 3 x 2 + x 2 + 2 3 + 4 + 2 2 3 + 4 3

Способ замены переменной при разложении многочлена на множители

При замене переменной производится понижение степени и разложение многочлена на множители.

Произвести разложение на множители многочлена вида x 6 + 5 x 3 + 6 .

По условию видно, что необходимо произвести замену y = x 3 . Получаем:

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6

Корни полученного квадратного уравнения равны y = – 2 и y = – 3 , тогда

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3

Необходимо применить формулу сокращенного умножения суммы кубов. Получим выражения вида:

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3 = = x + 2 3 x 2 – 2 3 x + 4 3 x + 3 3 x 2 – 3 3 x + 9 3

То есть получили искомое разложение.

Рассмотренные выше случаи помогут в рассмотрении и разложении многочлена на множители разными способами.

Разложение квадратного трехчлена на множители

Что значит разложение квадратного трехчлена на множители

Квадратный трехчлен представляет собой многочлен, который можно записать в виде:

Рассмотрим квадратные уравнения, которые записывают в общей форме:

a x 2 + b x + c = 0

Можно заметить, что в левой части расположен квадратный трехчлен.

В процессе решения многих задач целесообразно раскладывать квадратный трехчлен на множители. При этом начальный квадратный трехчлен следует приравнять к нулю и решать квадратное уравнение, согласно стандартному алгоритму.

Данное действие называют поиском корней квадратного трехчлена. Корни, которые получились, в виде х 1 и х 2 подставляют в выражение, являющееся результатом разложения:

а ( х – х 1 ) ( х – х 2 )

В результате для разложения квадратного трехчлена на множители путем поиска корней квадратного уравнения требуется применить следующую формулу:

a x 2 + b x + c = a ( x − x 1 ) ( x − x 2 )

Здесь в левой части записан начальный квадратный трехчлен.

В качестве примера можно рассмотреть задачу по разложению на множители заданного квадратного трехчлена:

В первую очередь следует определить корни данного квадратного трехчлена. При этом нужно приравнять исходный квадратный трехчлен к нулевому значению и найти решения для квадратного уравнения:

x 2 – 8 x + 12 = 0

Можно заметить, что коэффициент b — четный. По этой причине допустимо использовать в процессе решения формулы, предусмотренные для четного второго коэффициента. С целью сэкономить время определенные нюансы в вычислениях можно пропустить:

Далее можно использовать формулу:

a x 2 + b x + c = а ( х – х 1 ) ( х – х 2 )

Выполним замену выражения a x 2 + b x + c , которое записано в левой части уравнения, квадратным трехчленом из условия задачи x 2 – 8 x + 12 . В правую часть при этом можно записать полученные значения, то есть а = 1 , х 1 = 6 , х 2 = 2 . В результате:

x 2 − 8 x + 12 = 1 ( x − 6 ) ( x − 2 ) = ( x − 6 ) ( x − 2 )

При а = 1, как в этом случае, запись решения допустимо сократить:

x 2 − 8 x + 12 = ( x − 6 ) ( x − 2 )

С целью доказательства правильности разложения квадратного трехчлена на множители следует раскрыть скобки в правой части полученного уравнения, то есть в выражении со знаками минуса ( x − 6 ) ( x − 2 ) . Когда ошибки отсутствуют, в результате получится квадратный трехчлен x 2 − 8 x + 12 :

( x − 6 ) ( x − 2 ) = x 2 − 6 x − 2 x + 12 = x 2 − 8 x + 12

Закрепить материал можно на примере второй самостоятельной задачи. Предположим, что имеется некий квадратный трехчлен, который требуется разложить на множители:

2 x 2 − 14 x + 24

Необходимо приравнять квадратный трехчлен к нулевому значению и найти корни уравнения:

2 x 2 − 14 x + 24 = 0

По аналогии с прошлым примером здесь коэффициент b обладает четным значением. В связи с этим допускается применять в процессе решения формулы для четного второго коэффициента:

Далее необходимо записать равенство, состоящее из квадратного трехчлена 2 x 2 − 14 x + 24 и выражения а ( х – х 1 ) ( х – х 2 ) . Переменные а, х 1 и х 2 следует заменить соответствующими значениями. Заметим, что а = 2 . В итоге получим:

2 x 2 − 14 x + 24 = 2 ( x − 4 ) ( x − 3 )

В процессе проверки нужно избавиться от скобок в правой части равенства, которое получилось. Если действия выполнены верно, то результатом станет квадратный трехчлен 2 x 2 − 14 x + 24 :

2 ( x − 4 ) ( x − 3 ) = 2 ( x 2 − 4 x − 3 x + 12 ) = 2 ( x 2 − 7 x + 12 ) = 2 x 2 − 14 x + 24

Определение, как это работает, теорема

Квадратный трехчлен является многочленом в виде:

a x 2 + b x + c , если a ≠ 0

Примеры квадратных трехчленов:

Свое название квадратный трехчлен получил в связи с тем, что самая большая степень в этом случае представляет собой квадрат. С другой стороны, в состав квадратного трехчлена входят трое слагаемых, то есть одночленов. В результате получается квадратный трехчлен:

Трехчлены, которые не являются квадратными:

x 3 – 3 x 2 – 5 x + 6 − кубический четырехчлен.

2 x + 1 − линейный двучлен.

Теорема Виета: корни уравнения x 2 + b x + c = 0 в сумме равны второму коэффициенту с противоположным знаком, а произведение корней соответствует свободному члену.

Разложить квадратный трехчлен на множители можно путем замены коэффициентов квадратного трехчлена теоремой Виета. Далее следует выполнить тождественные преобразования.

Рассмотрим пример, в котором коэффициент а квадратного трехчлена равен 1:

Когда квадратное уравнение является приведенным, теорема Виета принимает следующий вид:

В результате приведенный квадратный трехчлен x 2 + b x + c можно разложить на множители. В первую очередь следует выразить b из уравнения х 1 + х 2 = – b путем умножения обеих его частей на -1:

Переменную с, используя теорему Виета, выражать нет необходимости, так как она уже выражена. Нужно лишь переставить местами части уравнения:

На следующем этапе следует выполнить подстановку выраженных переменных b и c в квадратный трехчлен x 2 + b x + c :

Раскрыть скобки следует там, где это представляется возможным:

Полученное выражение можно разложить на множители, используя метод группировки. В рассматриваемом примере целесообразно выполнить группировку первого и второго членов, третьего и четвертого членов. В результате:

Из первых скобок следует вынести общий множитель х , а вторые скобки избавить от общего множителя – х 2 :

Можно заметить, что выражение ( х – х 1 ) представляет собой общий множитель. Его можно вынести за пределы скобок:

x 2 + b x + c уровнялось с ( x − x 1 ) ( x − x 2 ) :

x 2 + b x + c = ( x − x 1 ) ( x − x 2 )

В рассмотренном примере начальный квадратный трехчлен был приведенным. При этом коэффициент а равен единице. Поэтому такой коэффициент допускается не учитывать.

В другом случае коэффициент а не равен 1. Тогда в формуле разложения появляется коэффициент а перед скобками:

a x 2 + b x + c = a ( x − x 1 ) ( x − x 2 )

В том случае, когда требуется решить не приведенное квадратное уравнение, то есть вида a x 2 + b x + c = 0 , теорема Виета в записи выглядит следующим образом:

Такая запись объясняется применимостью теоремы Виета лишь в случае с приведенными квадратными уравнениями. Преобразовать уравнение a x 2 + b x + c = 0 в вид приведенного можно путем деления обеих его частей на а:

Разложение квадратного трехчлена a x 2 + b x + c на множители выполняют путем замены b и c на соответствующие выражения из теоремы Виета. При этом следует воспользоваться равенствами:

В первую очередь следует выразить b и c. В первом равенстве нужно перемножить компоненты уравнения на а. Далее необходимо умножить на -1 обе части равенства, которое получилось в результате предыдущего действия.

Затем нужно выразить с из второго равенства путем умножения обеих его частей на а:

С помощью подстановки выраженных переменных b и с в квадратный трехчлен a x 2 + b x + c получим:

Заметим, что переменные b и c заменили выражениями − a x 1 − a x 2 и a x 1 x 2 , которые были выражены из теоремы Виета. Далее нужно избавиться из скобок там, где это допустимо:

Полученное выражение можно разложить на множители с помощью метода группировки. В этом примере целесообразно сгруппировать первый и второй члены, третий и четвертый члены:

Из первых скобок необходимо вынести единый множитель ах, а из вторых скобок вынести общий множитель – а х 2 :

Заметим, что х – х 1 также представляет собой общий множитель. Его аналогичным образом можно вынести за скобки:

Во вторых скобках имеется общий множитель а. Данный множитель также можно вынести за скобки в начало выражения:

a x 2 + b x + c = a ( x − x 1 ) ( x − x 2 )

Заметим, что в случае отсутствия корней у квадратного трехчлена не представляется возможным выполнить разложение на множители. В действительности, когда корней нет, их не получится подставить в выражение a ( x − x 1 ) ( x − x 2 ) на место переменных x 1 и x 2 .

Когда у квадратного трехчлена имеется единственный корень, данный корень одновременно подставляют в х 1 и х 2 . К примеру, у квадратного трехчлена x 2 + 4 x + 4 есть только один корень -2:

В таком случае значение -2 при разложении на множители заменит х 1 и х 2 . С другой стороны, значение а соответствует 1. По этой причине этот коэффициент допустимо не записывать:

Внутренние скобки целесообразно раскрыть. В результате:

В том случае, когда ответ требуется представить в сокращенном виде, можно последнее выражение записать, как ( x + 2 ) 2 . Это объясняется выражением ( x + 2 ) ( x + 2 ) , которое является результатом умножения двух сомножителей, каждый из которых соответствует ( x + 2 ) :

Порядок разложения на множители квадратного трехчлена

Корень квадратного трехчлена является таким значением переменной х, при котором этот трехчлен принимает нулевое значение.

Трехчлен x 2 – 2 x + 1 имеет корень 1. Это объясняется тем, что: 1 2 – 2 · 1 + 1 = 0 .

Трехчлен x 2 + 2 x – 3 обладает корнями 1 и -3, так как 1 2 + 2 – 3 = 0 и ( – 3 ) 2 – 6 – 3 = 9 – 9 = 0 .

Вычислить корни квадратного трехчлена можно путем решения соответствующего квадратного уравнения.

Квадратный трехчлен x 2 – 2 x + 1 нужно приравнять к нулю и решить уравнение x 2 – 2 x + 1 = 0 :

x = 2 – 0 2 = 2 2 = 1

В результате корень равен 1.

Некий квадратный трехчлен в виде a x 2 + b x + c можно разложить таким образом: a ( x – x 1 ) ( x – x 2 ) , когда дискриминант уравнения a x 2 + b x + c = 0 больше нуля. x 1 и x 2 являются корнями этого же уравнения.

Квадратный трехчлен 3 x 2 + 13 x – 10 нужно разложить на множители. Квадратное уравнение 3 x 2 + 13 x – 10 = 0 обладает дискриминантом, который равен 289, и корнями в виде -5 и 2 3 . В результате:

3 x 2 + 13 x – 10 = 3 ( x + 5 ) ( x – 2 3 )

Проверить правильность действий можно путем раскрытия скобок. В итоге получится начальный трехчлен.

При нулевом дискриминанте уравнения a x 2 + b x + c = 0 квадратный трехчлен a x 2 + b x + c допустимо записать в виде a ( x – x 1 ) 2 .

В качестве примера можно рассмотреть трехчлен x 2 + 6 x + 9 . Квадратное уравнение x 2 + 6 x + 9 = 0 имеет дискриминант, равный нулю. Один возможный корень составляет -3. Таким образом:

x 2 + 6 x + 9 = ( x + 3 ) 2

Коэффициент а равен единице, поэтому его можно не ставить перед скобкой.

Квадратный трехчлен a x 2 + b x + c невозможно разложить на множители при дискриминанте уравнения a x 2 + b x + c = 0 , который меньше нуля.

К примеру, трехчлены x 2 + x + 4 и – 5 x 2 + 2 x – 1 не получится разложить на множители. Это связано с тем, что дискриминанты меньше по сравнению с нулем.

Примеры решения заданий для 9 класса

Требуется разложить трехчлен на множители:

2 x 2 – 11 x + 12

Запишем квадратное уравнение:

2 x 2 – 11 x + 12 = 0

Найдем его корни:

D = 11 2 – 4 · 2 · 12 = 121 – 96 = 25 > 0

x 1 = 11 – 5 4 = 1 , 5 ; x 2 = 11 + 5 4 = 4

2 x 2 – 11 x + 12 = 2 ( x – 1 , 5 ) ( x – 4 )

Ответ: 2 ( x – 1 , 5 ) ( x – 4 )

Ответ можно записать и в другой форме: ( 2 x – 3 ) ( x – 4 )

Квадратный трехчлен разложили на множители:

5 x 2 + 33 x + 40 = 5 ( x + 5 ) ( x – a )

Требуется определить а.

5 x 2 + 33 x + 40 = 0

D = 33 2 – 4 · 5 · 40 = 1089 – 800 = 289 = 17 2

x 1 = – 33 – 17 10 = – 5

x 2 = – 33 + 17 10 = – 1 , 6

5 x 2 + 33 x + 40 = 5 ( x + 5 ) ( x + 1 , 6 )

Нужно разложить квадратный трехчлен 2 х 2 – 9 х + 7 на множители.

Запишем квадратное уравнение:

2 х 2 – 9 х + 7 = 0

Решим это уравнение:

D = b 2 – 4 a c = 81 – 4 · 2 · 7 = 25 ;

x 1 = ( 9 + 5 ) / 4 = 3 , 5

x 2 = ( 9 – 5 ) / 4 = 1

После определения корней можно их подставить в уравнение:

2 х 2 – 9 х + 7 = 2 ( x – 3 , 5 ) ( x – 1 )

Ответ: 2 ( x – 3 , 5 ) ( x – 1 )

Квадратный трехчлен х 2 – 4 х + 4 требуется разложить на множители.

Запишем квадратное уравнение:

Данное уравнение является приведенным, поэтому решать его следует через дискриминант, либо с помощью теоремы Виета. Воспользуемся теоремой. Согласно ей, при умножении корней должно получиться число 4, как и при их сложении. Таким образом:

Как разложить на множители квадратный трехчлен: формула

Разложение многочленов для получения произведения иногда кажется запутанным. Но это не так сложно, если разобраться в процессе пошагово. В статье подробно рассказано, как разложить на множители квадратный трехчлен.

Понятие и определение

Многим непонятно, как разложить на множители квадратный трехчлен, и для чего это делается. Сначала может показаться, что это бесполезное занятие. Но в математике ничего не делается просто так. Преобразование нужно для упрощения выражения и удобства вычисления.

Многочлен, имеющий вид – ax²+bx+c, называется квадратным трехчленом. Слагаемое «a» должно быть отрицательным или положительным. На практике это выражение называется квадратным уравнением. Поэтому иногда говорят и по-другому: как разложить квадратное уравнение.

Интересно! Квадратным многочлен называют из-за самой его большой степени – квадрата. А трехчленом из-за 3-х составных слагаемых.

Некоторые другие виды многочленов:

• линейный двучлен (6x+8),
• кубический четырехчлен (x³+4x²-2x+9).

Разложение квадратного трехчлена на множители

Сначала выражение приравнивается к нулю, затем нужно найти значения корней x1 и x2. Корней может не быть, может быть один или два корня. Наличие корней определяется по дискриминанту. Его формулу надо знать наизусть: D=b²-4ac.

Если результат D получается отрицательный, корней нет. Если положительный – корня два. Если в результате получился ноль – корень один. Корни тоже высчитываются по формуле.

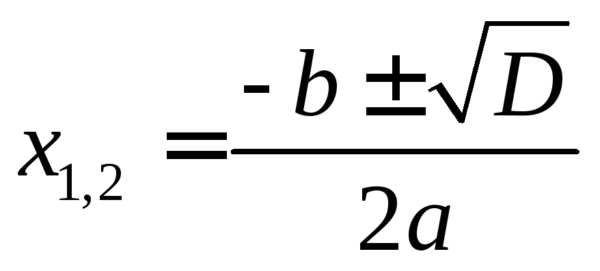
Если при вычислении дискриминанта получается ноль, можно применять любую из формул. На практике формула просто сокращается: -b / 2a.

Формулы для разных значений дискриминанта различаются.

Если D положительный:

Если D равен нулю:

Если выражение отрицательное, считать ничего не нужно.

Это интересно! Как найти и чему будет равна длина окружности

Онлайн калькуляторы

В интернете есть онлайн калькулятор. С его помощью можно выполнить разложение на множители. На некоторых ресурсах предоставляется возможность посмотреть решение пошагово. Такие сервисы помогают лучше понять тему, но нужно постараться хорошо вникнуть.

Если тема понятна, рекомендуется использовать онлайн калькулятор для проверки решения.

Полезное видео: Разложение квадратного трехчлена на множители

Примеры

Предлагаем просмотреть простые примеры, как разложить квадратное уравнение на множители.

Пример 1

Здесь наглядно показано, что в результате получится два x, потому что D положительный. Их и нужно подставить в формулу. Если корни получились отрицательные, знак в формуле меняется на противоположный.

Нам известна формула разложения квадратного трехчлена на множители: a(x-x1)(x-x2). Ставим значения в скобки: (x+3)(x+2/3). Перед слагаемым в степени нет числа. Это значит, что там единица, она опускается.

Это интересно! Как раскрыть модуль действительного числа и что это такое

Пример 2

Этот пример наглядно показывает, как решать уравнение, имеющее один корень.

Подставляем получившееся значение:

Пример 3

Сначала вычислим дискриминант, как в предыдущих случаях.

Дискриминант отрицательный, значит, корней нет.

После получения результата стоит раскрыть скобки и проверить результат. Должен появиться исходный трехчлен.

Альтернативный способ решения

Некоторые люди так и не смогли подружиться с дискриминантом. Можно еще одним способом произвести разложение квадратного трехчлена на множители. Для удобства способ показан на примере.

Мы знаем, что должны получиться 2 скобки: (_)(_). Когда выражение имеет такой вид: x²+bx+c, в начале каждой скобки ставим x: (x_)(x_). Оставшиеся два числа – произведение, дающее «c», т. е. в этом случае -10. Узнать, какие это числа, можно только методом подбора. Подставленные числа должны соответствовать оставшемуся слагаемому.

Это интересно! Уроки математики: умножение на ноль главное правило

К примеру, перемножение следующих чисел дает -10:

Далее выполняем подбор и смотрим, чтобы получилось выражение, которое было сначала:

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. Нет.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. Нет.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. Нет.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Подходит.

Значит, преобразование выражения x2+3x-10 выглядит так: (x-2)(x+5).

Важно! Стоит внимательно следить за тем, чтобы не перепутать знаки.

Разложение сложного трехчлена

Если «a» больше единицы, начинаются сложности. Но все не так трудно, как кажется.

Чтобы выполнить разложение на множители, нужно сначала посмотреть, возможно ли что-нибудь вынести за скобку.

Например, дано выражение: 3x²+9x-30. Здесь выносится за скобку число 3:

3(x²+3x-10). В результате получается уже известный трехчлен. Ответ выглядит так: 3(x-2)(x+5)

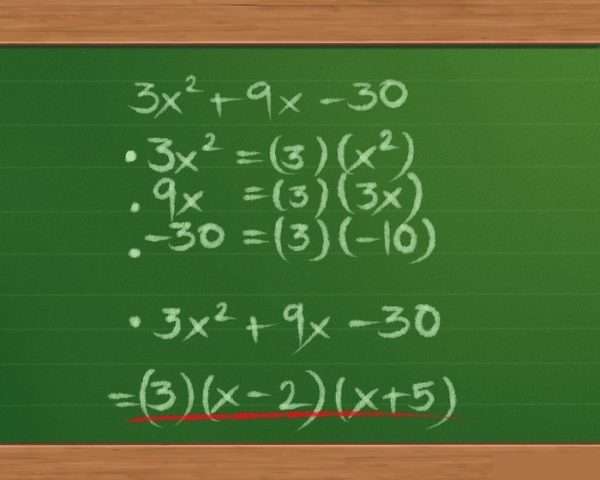
Как раскладывать, если слагаемое, которое находится в квадрате отрицательное? В данном случае за скобку выносится число -1. К примеру: -x²-10x-8. После выражение будет выглядеть так:

Схема мало отличается от предыдущей. Есть лишь несколько новых моментов. Допустим, дано выражение: 2x²+7x+3. Ответ также записывается в 2-х скобках, которые нужно заполнить (_)(_). Во 2-ю скобку записывается x, а в 1-ю то, что осталось. Это выглядит так: (2x_)(x_). В остальном повторяется предыдущая схема.

Число 3 дают числа:

Решаем уравнения, подставляя данные числа. Подходит последний вариант. Значит, преобразование выражения 2x²+7x+3 выглядит так: (2x+1)(x+3).

Это интересно! Считаем правильно: как находить процент от суммы и числа

Другие случаи

Преобразовать выражение получится не всегда. При втором способе решение уравнения не потребуется. Но возможность преобразования слагаемых в произведение проверяется только через дискриминант.

Стоит потренироваться решать квадратные уравнения, чтобы при использовании формул не возникало трудностей.

Полезное видео: разложение трехчлена на множители

Вывод

Пользоваться можно любым способом. Но лучше оба отработать до автоматизма. Также научиться хорошо решать квадратные уравнения и раскладывать многочлены на множители нужно тем, кто собирается связать свою жизнь с математикой. На этом строятся все следующие математические темы.

Как разложить квадратный трёхчлен на множители?

Мир погружён в огромное количество чисел. Любые исчисления происходят с их помощью.

Люди учат цифры для того, чтобы в дальнейшей жизни не попадаться на обман. Необходимо уделять огромное количество времени, чтобы быть образованным и рассчитать собственный бюджет.

Математика — это точная наука, которая играет большую роль в жизни. В школе дети изучают цифры, а после, действия над ними.

Действия над числами бывают совершенно разными: умножение, разложение, добавление и прочие. Помимо простых формул, в изучении математики используют и более сложные действия. Существует огромное количество формул, по которым узнают любые значения.

В школе, как только появляется алгебра, в жизнь школьника добавляются формулы упрощения. Бывают уравнения, когда неизвестных числа два, но найти простым способом не получится. Трёхчлен — соединение трёх одночленов, с помощью простого метода отнимания и добавления. Трёхчлен решается с помощью теоремы Виета и дискриминанта.

Формула разложения квадратного трёхчлена на множители

Существуют два правильных и простых решения примера:

• дискриминант;
• теорема Виета.

Квадратный трёхчлен имеет неизвестный в квадрате, а также число без квадрата. Первый вариант для решения задачи использует формулу Виета. Это простая формула, если цифры, что стоят перед неизвестным, будут минимальным значением.

Для других уравнений, где число стоит перед неизвестным, уравнение необходимо решать через дискриминант. Это более сложное решение, но используют дискриминант намного чаще, нежели теорему Виета.

Изначально, для нахождения всех переменных уравнения необходимо возвести пример к 0. Решение примера можно будет проверить и узнать правильно ли подстроены числа.

Дискриминант

1. Необходимо приравнять уравнение к 0.

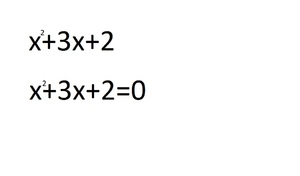
2. Каждое число перед х будет названо числами a, b, c. Так как перед первым квадратным х нет числа, то оно приравнивается к 1.

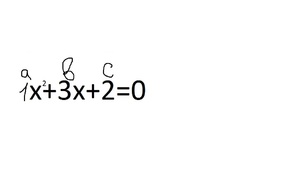
3. Теперь решение уравнения начинается через дискриминант:

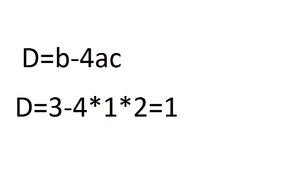
4. Теперь нашли дискриминант и находим два х. Разница заключается в том, что в одном случае перед b будет стоять плюс, а в другом минус:

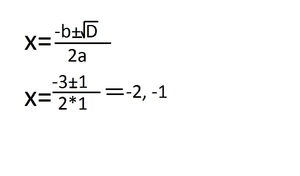
5. По решению два числа получилось -2 и -1. Подставляем под первоначальное уравнение:

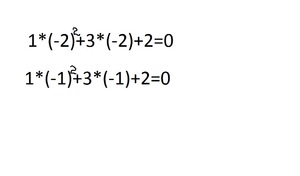
6. В этом примере получилось два правильных варианта. Если оба решения подходят, то каждое из них является истинным.

Через дискриминант решают и более сложные уравнение. Но если само значение дискриминанта будет меньше 0, то пример неправильный. Дискриминант при поиске всегда под корнем, а отрицательное значение не может находиться в корне.

Теорема Виета

Применяется для решения лёгких задач, где перед первым х не стоит число, то есть a=1. Если вариант совпадает, то расчёт проводят через теорему Виета.

Для решения любого трёхчлена необходимо возвести уравнение к 0. Первые шаги у дискриминанта и теоремы Виета не отличаются.

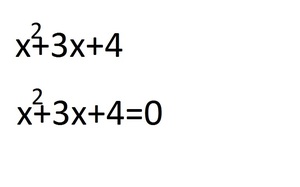
2. Теперь между двумя способами начинаются отличия. Теорема Виета использует не только «сухой» расчёт, но и логику и интуицию. Каждое число имеет свою букву a, b, c. Теорема использует сумму и произведение двух чисел.

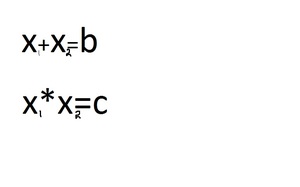
Запомните! Число b всегда при добавлении стоит с противоположным знаком, а число с остаётся неизменным!

Подставляя значения данные в примере, получаем:

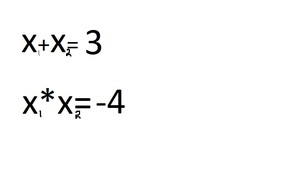
3. Методом логики подставляем наиболее подходящие цифры. Рассмотрим все варианты решения:

1. Цифры 1 и 2. При добавлении получаем 3, но если умножить, то не получится 4. Не подходит.
2. Значение 2 и -2. При умножении будет -4, но при добавлении получается 0. Не подходит.
3. Цифры 4 и -1. Так как в умножении стоит отрицательное значение, значит, одно из чисел будет с минусом. При добавлении и умножении подходит. Правильный вариант.

4. Остаётся только проверить, раскладывая числа, и посмотреть правильность подобранного варианта.

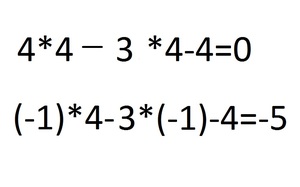
5. Благодаря онлайн-проверке мы узнали, что -1 не подходит по условию примера, а значит является неправильным решением.

При добавлении отрицательного значения в примере, необходимо цифру заносить в скобки.

В математике всегда будут простые задачи и сложные. Сама наука включает в себя разнообразие задач, теорем и формул. Если понимать и правильно применять знания, то любые сложности с вычислениями будут пустяковыми.

Математика не нуждается в постоянном запоминании. Нужно научится понимать решение и выучить несколько формул. Постепенно, по логическим выводам, можно решать похожие задачи, уравнения. Такая наука может с первого взгляда показаться очень тяжёлой, но если окунутся в мир чисел и задач, то взгляд резко изменится в лучшую сторону.

Технические специальности всегда остаются самыми востребованными в мире. Сейчас, в мире современных технологий, математика стала незаменимым атрибутом любой сферы. Нужно всегда помнить о полезных свойствах математики.

Разложение трёхчлена с помощью скобки

Кроме решения привычными способами, существует ещё один — разложение на скобки. Используют с применением формулы Виета.

1. Приравниваем уравнение к 0.

2. Корни уравнения остаются такими же, но вместо нуля теперь используют формулы разложения на скобки.

Как разложить на множители квадратный трехчлен

Математика

Что такое квадратный трехчлен и как разложить на множители квадратный трехчлен.

Квадратный трехчлен

Квадратным трехчленом называют выражение вида

Разложить на множители квадратный трехчлен — это значит, записать его в виде произведения.

Разложение на множители квадратного трехчлена

Чтобы разложить на множители квадратный трехчлен используем следующее правило:

, где , где и — корни уравнения — корни уравнения .

Таким образом, нам нужно решить квадратное уравнение и затем найденные корни подставить сюда: и затем найденные корни подставить сюда:

Рассмотрим на примере: требуется разложить на множители квадратный трехчлен:

Решим уравнение: , находим дискриминант , находим дискриминант , тогда корни уравнения: и и , тогда по формуле разложения на множители получаем:

Давайте еще рассмотрим один пример: пусть требуется разложить на линейные множители квадратный трехчлен . Находим корни этого уравнения . Находим корни этого уравнения .

Находим дискриминант уравнения. Если вы забыли как найти дискриминант посмотрите здесь.

, отсюда корни уравнения , отсюда корни уравнения и . И разложение квадратного трехчлена на множители мы запишем так: . И разложение квадратного трехчлена на множители мы запишем так: .

Краткая схема разложения на множители квадратного трехчлена

Схема не сложная. Но иногда могут встречаться затруднения. Например — что если корень получился один, а не два. На самом деле в квадратном уравнении всегда два корня. Об этом нам «говорит» степень 2, над . Это означает, что если у вас дискриминант равен нулю, вы получаете не один корень, а два совпадающих друг с другом корня. И разложение на множители будет выглядеть так:

.

Например: квадратный трехчлен при равенстве нулю имеет два совпадающих корня при равенстве нулю имеет два совпадающих корня и раскладывать на множители мы будем его так

.

В дальнейшем, следует помнить — что в кубическом уравнении 3 корня, в биквадратном — 4. Сколько степеней в уравнении, столько и корней у него должно быть. Другое дело, что некоторые из них, и даже все, могут совпадать в значении. Геометрический смысл такого совпадения в том, что график кривой, которая описывается уравнением, будет лишь касаться оси .

Итак, давайте выполним следующее задание: нужно разложить на множители квадратных трехчлен .

Найдем корни уравнения . Для этого сначала найдем дискриминант . Для этого сначала найдем дискриминант .

Тогда корни уравнения: . И . И .

Итак, получили и и . Подставляя в формулу разложения на множители квадратного трехчлена, получим:

.

Теперь вы знаете как разложить на множители квадратный трехчлен. Успехов в учебе!

Как написать студенческую работу, чтобы её 100% приняли?

Возникают ситуации, когда очень сложно сделать работу, когда совершенно не понятно каков должен быть конечный результат. В таких случаях лучше не тратить лишние время и нервы, а обращаться к знающим людям.

8.2.5. Разложение квадратного трехчлена на линейные множители

Решение. Найдем корни квадратного уравнения: 2x 2 -7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b 2 -4ac=(-7) 2 -4∙2∙(-15)=49+120=169=13 2 >0; 2 действительных корня.

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

2x 2 -7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x 2 -7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x 2 -7x-15=(2х+3)(х-5).

Пример 2). 3x 2 +2x-8.

Решение. Найдем корни квадратного уравнения:

a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

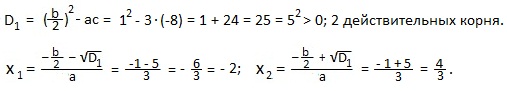
Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x 2 +2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x 2 +2x-8=(х+2)(3х-4).

Пример 3). 5x 2 -3x-2.

Решение. Найдем корни квадратного уравнения:

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

5x 2 -3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x 2 -3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x 2 -3x-2=(х-1)(5х+2).

Пример 4). 6x 2 +x-5.

Решение. Найдем корни квадратного уравнения:

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x 2 +x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x 2 +x-5=(х+1)(6х-5).

Пример 5). x 2 -13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x 2 -13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b 2 -4ac=13 2 -4∙1∙12=169-48=121=11 2 .

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Ответ: x 2 -13x+12=(х-1)(х-12).

Пример 6). x 2 -4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».