Абсолютная величина. Модуль.
Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.
Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).
Абсолютное значение величины – это само число (без знака), как например: температура, давление, скорость и т. п. Модуль – это число без направления, например: давление, скорость, сила и т. п.
Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.
Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:
- Индивидуальная абсолютная величина — характеризует единицу совокупности,
- Суммарная абсолютная величина — характеризует группу единиц или всю совокупность.
Свойства модуля.
- Модулю присущи некоторые характерные результаты – свойства модуля.
- Модуль числа не бывает числом меньше нуля. Обоснование этого свойства: модуль числа – это расстояние, а расстояние не выражается числом ниже нуля.
- Модуль числа = 0 только в том случае, если это число является нулем. Модуль нуля – это нуль по определению. Нуль – это начало отсчета, ни одна больше точка на координатной прямой нулем не является. Исходя из этого, каждому числу, не равному нулю, соответствует точка, не являющаяся началом отсчета. Значит, расстояние начало отсчета – любая точка, не соответствующая точке O, не равно нулю, т.к. расстояние между 2 точка и равно нулю только если они совпадают. Из этого следует, что нулю равен только модуль нуля.
- Противоположные числа имеют одинаковые модули, т.е. , для каждого числа a. Так и есть, 2 точки на координатной прямой, координаты которых – противоположные числа, расположены на равном расстоянии от начала отсчета, т.о. модули противоположных чисел одинаковы.
- По определению модуль произведения чиселa и b равен либо a·b, если , либо −(a·b), если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.
- Модуль частного от деленияa на b = частному от деления модуля числа a на модуль числа b, т.е.,

.
Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.
Основные свойства абсолютной величины.
Вещественные числа.
Комплексные числа.
Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:
Как для вещественных, так и для комплексных a, b имеют место соотношения:
Модуль числа

Разберем сегодня, что значит модуль числа, как считать модуль и как обозначается модуль в математике. А также его свойства и, конечно же, примеры.
О чем эта статья:
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
- |a| = a, если a > 0
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
- |0| = 0, если a = 0
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
- |a b| = |a| |b|, когда
−(a · b), когда a · b < 0
7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a – b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a – b| = |b – a|.
Решим уравнение: |a – 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 – и это один ответ, а также к 3 мы прибавили 4 – и это второй ответ.
Решим неравенство: |a + 7| < 4.
Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:
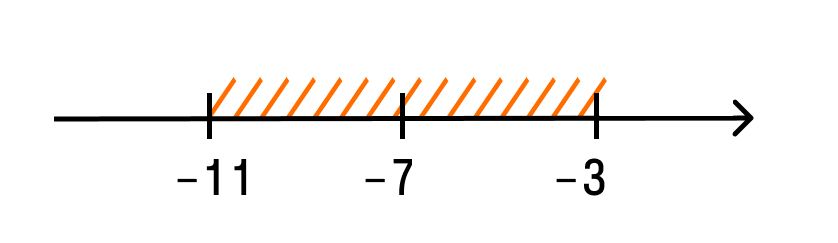
Ответ в данном случае будет таким: (−11; −3).
Решим неравенство: |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
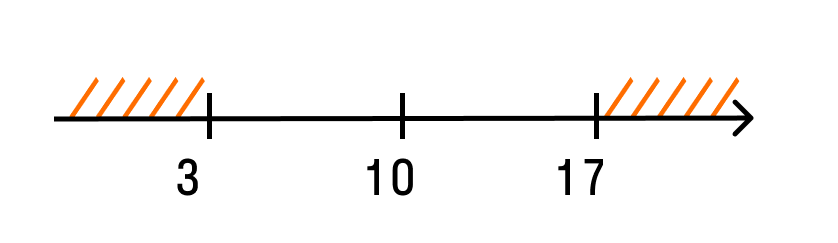
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.
При этом, √ a 2 = |a|.
По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .
Оно равно a при а > 0 и −а, при а < 0 , т. е. как раз |a|.
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Что такое модуль числа в математике

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a|.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

- Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
- Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.
Графически это можно выразить следующим образом: |a| = OA.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

- Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
- Такое же правило распространяется и на показатель степени выражения.
Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5, если, А больше или равняется нулю.
5-А, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Уравнения с модулем
Модуль числа — абсолютная величина, демонстрирующая удаленность точки от начала координат.
В том случае, когда число является отрицательным, его модуль соответствует числу, ему противоположному. Для неотрицательного числа модуль равен этому числу.
| x | = x , x ≥ 0 – x , x < 0
Уравнения с модулем являются такими уравнениями, в составе которых имеется переменная, заключенная в знак модуля.
Самое простое уравнение с модулем |f(x)|=a является равносильным совокупности
Здесь a>0. При а отрицательном у такого уравнения отсутствует решение.
Уравнения с модулем могут быть предложены в качестве самостоятельного задания. Кроме того, подобные выражения нередко образуются в процессе решения других видов уравнений, к примеру, квадратных или иррациональных.
Разберем подробное решение квадратного уравнения:
Заметим, что справа имеется квадрат числа 4:
На первый взгляд, нужно избавиться от квадратов, чтобы получить линейное уравнение. С другой стороны, существует правило:
Вычисления следует продолжить с учетом записанной формулы. Тогда получим уравнение с модулем:
x 2 = 4 2 ⇔ x 2 = 4 2 ⇔ x = 4
Рассмотрим для тренировки пример, когда уравнения с модулем появляются при решении иррациональных уравнений. Например, дано уравнение:
2 x – 1 2 = 9 x 2 + 12 x + 4
Согласно стандартному алгоритму действий, в этом случае потребуется выполнить действия:
- перенос слагаемых;
- приведение подобных;
- решение квадратного уравнения, например, с помощью дискриминанта.
Второй вариант решения предусматривает использование формулы сокращенного умножения квадрат суммы:
9 x 2 + 12 x + 4 = 3 x + 2 2
Преобразуем сложное уравнение:
2 x – 1 2 = 3 x + 2 2
На первый взгляд, можно избавиться от квадратов и решить линейное уравнение. Однако:
В результате получим:
2 x – 1 2 = 3 x + 2 2 ⇔ 2 x – 1 = 3 x + 2 .
При решении уравнений, которые содержат модуль, необходимо помнить свойства модуля:
- Модуль числа является неотрицательным числом: x ≥ 0 , x = 0 ⇔ x = 0 .
- Противоположные числа равны друг другу по модулю: – x = x .
- Произведение пары или более чисел по модулю равно произведению модулей этих чисел: x · y = x · y .
- Частное пары чисел по модулю равно частному модулей этих чисел: x y = x y , y ≠ 0 .
- Сумма чисел по модулю в любом случае меньше или равна сумме модулей данных чисел: x + y ≤ x + y .
- Постоянный множитель, который больше нуля, допустимо вынести за знак модуля: c x = c · x при c > 0 .
- Квадрат какого-то числа по модулю равен квадрату данного числа: x 2 = x 2 .
Руководствуясь перечисленными свойствами модуля, рассмотрим решение уравнения:
Заметим, что x равен x при x больше либо равно нулю. Значение –x возможно, когда x является отрицательным числом. Таким образом:
x = 7 ⇔ x = 7 , п р и x ≥ 0 – x = 7 , п р и x < 0 ⇔ x = 7 x = - 7
Рассмотрим несколько иное уравнение:
В этом случае логика такая же, как в предыдущем примере:
x = – 7 ⇔ x = – 7 , при x ≥ 0 – x = – 7 , при x < 0 ⇔ x = - 7 x ≥ 0 ⇒ р е ш е н и я н е т x = 7 x < 0 ⇒ р е ш е н и я н е т
Способы решения уравнений с модулями для 10 и 11 классов
Существует три основных вида уравнений с модулем, которые предусматривают определенные подходы к решению:
- Уравнения x = a . x = a ⇔ x = a , п р и x ≥ 0 – x = a , п р и x < 0 ⇔ x = a x = - a .
- Уравнения вида x = y . x = y ⇔ y ≥ 0 x = y x = – y
Примеры решения задач с объяснением
Уравнения, которые содержат модуль и имеют вид |x| = |a|, решают с помощью определения модуля.
Рассмотрим в качестве примера:
Определим x . Когда x ≥ 0 , значение равно х . Если x
x = 5 ⇔ x = 5 при x ≥ 0 – x = 5 при x < 0 ⇔ x = 5 x = - 5 .
Получим, что решением уравнения являются -5; 5.
Рассмотрим следующее задание, в рамках которого необходимо решить уравнение:
Воспользуемся стандартным алгоритмом:
Согласно первому свойству модуля:
x ≥ 0 , то есть модуль в любом случае не является отрицательным числом.
Можно обобщить рассмотренные действия и записать правило для решения уравнений, которые имеют вид x = a . Данное правило можно использовать в работе:
x = a ⇒ a ≥ 0 x = a x = – a .
Используя данное правило, решим уравнение:
По сравнению с предыдущим примером, здесь под знаком модуля записано иное выражение. Однако суть решения от этого не меняется. Зная правило, выполним замену:
x – 5 = 3 ⇔ 3 ≥ 0 x – 5 = 3 x – 5 = – 3 ⇒ x = 8 x = 2
Решим следующее уравнение:
Воспользуемся правилом и получим:
3 x – 5 = 3 ⇔ 3 ≥ 0 3 x – 5 = 3 3 x – 5 = – 3 ⇒ x = 8 3 x = 2 3
Далее рассмотрим решение уравнений, которые записаны в виде | x | = | y | .
При раскрытии модулей, согласно определению, возникнет необходимость во множестве проверок. Например, потребуется определить, какое число является положительным, а какое будет отрицательным. Полученную в результате систему в дальнейшем необходимо упростить.
Второй вариант решения подразумевает изначально краткую запись вычислений. Вспомним, что по свойству модуля:
Применим это свойство к нашему примеру и исключим знаки модулей из уравнения:
x = y ⇔ x 2 = y 2 ⇔ x 2 = y 2 ⇔ x 2 – y 2 = 0 ⇔
⇔ x – y x + y = 0 ⇔ x = y x = – y .
Рассмотрим еще несколько примеров.
Воспользуемся рассмотренным правилом применения свойства модуля, получим:
x + 1 = 2 x – 1 ⇔ x + 1 = 2 x – 1 x + 1 = – 2 x – 1 ⇔ x = 2 x = 0 .
Решение выполняем по аналогии с предыдущими заданиями:
2 x – 9 = 3 – x ⇔ 2 x – 9 = 3 – x 2 x – 9 = x – 3 ⇔ 3 x = 12 x = 6 ⇔ x = 4 x = 6 .
Разберем на примере, как решать уравнения вида | x | = y .
Заметим, что справа записана переменная, которая может быть положительным или отрицательным числом. Исходя из того, что модуль не может быть отрицательным числом, убедимся в том, что эта переменная также не является отрицательным числом:
x = y ⇔ y ≥ 0 x = y x = – y
Воспользуемся стандартным алгоритмом:
x + 1 = 1 – 2 x ⇔ 1 – 2 x ≥ 0 x + 1 = 1 – 2 x x + 1 = 2 x – 1 ⇔ x ≤ 1 2 x = 0 x = 2 ⇔ x = 0 .
Заметим, что без проверки на положительность части уравнения, которая записана с правой стороны, существуют риски появления посторонних корней в решении. К примеру, проверим x=2 путем подстановки в начальное уравнение x + 1 = 1 – 2 x :
2 + 1 = 1 – 2 · 2 ⇔ 3 = – 3 не является верным.
При решении уравнений с модулем также применяют метод интервалов. Данный способ следует применять в тех случаях, когда уравнение содержит более двух модулей.
Рассмотрим пример такого выражения:
x + 3 – 2 x – 1 = 1
Первый модуль имеет вид:
Согласно определению модуля, при раскрытии знака выражение под ним сохраняется без изменений, если:
После раскрытия знака модуля получим противоположный знак, когда:
x + 3 = x + 3 , если x + 3 ≥ 0 – x – 3 , если x + 3 < 0 .
По аналогии выполним преобразования второго модуля:
2 x – 1 = 2 x – 1 , если 2 x – 1 ≥ 0 1 – 2 x , если 2 x – 1 < 0 .
Сложность заключается в том, что требуется проанализировать много вариантов, то есть по два варианта для каждого из модулей. Всего получится четыре уравнения. А в том случае, когда модулей три, потребуется рассмотреть восемь уравнений. Возникает необходимость в сокращении числа вариантов.
Заметим, что в нашем примере не предусмотрено одновременное выполнение всех условий:
Данные условия противоречивы относительно друг друга. В связи с этим, нецелесообразно раскрывать второй модуль со знаком плюс, когда первый модуль раскрыт со знаком минус. В результате получилось избавиться от одного уравнения.
Обобщая эту информацию, можно записать алгоритм действий. В первую очередь следует вычислить корни выражений, заключенных под знаком модуля. В результате получаются такие х , при которых выражения принимают нулевые значения:
x + 3 = 0 ⇒ x = – 3 2 x – 1 = 0 ⇒ x = 1 2
С помощью стандартного способа интервалов можно отметить на координатной прямой корни выражений, которые находятся под модулями, и расставить знаки. Далее для каждого из полученных интервалов нужно составить и решить уравнение.
В этом случае оба модуля раскрываются со знаком минус:
– x + 3 + 2 x – 1 = 1 ⇔ – x – 3 + 2 x – 1 = 1 ⇔ x = 5 > – 3 является сторонним корнем.
В данном выражении первый модуль раскроется со знаком плюс, а второй — со знаком минус:
x + 3 + 2 x – 1 = 1 ⇔ x + 3 + 2 x – 1 = 1 ⇔ x = – 1 3 полученный корень соответствует своему интервалу.
Теперь для обоих модулей будет записан знак плюс:
x + 3 – 2 x – 1 = 1 ⇔ x + 3 – 2 x + 1 = 1 ⇔ x = 3 данный корень также подходит для решения.
Выполним проверку корней. В первом случае корень посторонний:
x = 5 : 5 + 3 – 2 · 5 – 1 = 8 – 9 = – 1 ≠ 1
Второй корень является решением:
x = – 1 3 : – 1 3 + 3 – 2 · – 1 3 – 1 = 8 3 – 5 3 = 1 .
Третий корень также является решением:
x = 3 : 3 + 3 – 2 · 3 – 1 = 6 – 5 = 1 .
Таким образом, запишем ответ: – 1 3 ; 3 .
Существует ряд уравнений, в которых модуль расположен под знаком модуля. К примеру:
В этом случае следует раскрывать модули поочередно. Проанализируем два варианта решения.
Первое решение подразумевает вычисления для уравнения, которое имеет вид:
f x = a ⇔ f x = a f x = – a
Здесь f x является подмодульным выражением. Применительно к нашей задаче, это:
x – 5 = 3 ⇔ x – 5 = 3 x – 5 = – 3 ⇔ x = 8 x = 2
Получена пара простейших уравнений аналогичного вида, то есть:
x = 8 x = – 8 x = 2 x = – 2
Данные четыре числа являются решениями. Проверить это можно путем подстановки ответов в исходное уравнение.
Второй вариант решения является универсальным и позволяет справиться с нестандартными задачами.
Раскроем сначала внутренние модули:
Начальное уравнение будет записано, как пара уравнений:
Задачи для самостоятельного решения
Найти корни уравнения:
Здесь нужно возвести в квадрат все части выражения, сохраняя знак плюса справа. Тогда получится система:
Найдем корни квадратного уравнения:
3 x 2 – 18 x + 24 = 0
В процессе потребуется сократить уравнение на 3:
D = ( – 6 ) 2 – 4 · 1 · 8 = 36 – 32 = 4
Заметим, что D>0. В таком случае у уравнения есть пара решений, которые можно определить так:
x 1 , 2 = – b ± D 2 a ⇒ x 1 , 2 = 6 ± 4 2 · 1 ⇒ x 1 , 2 = 6 ± 2 2 ⇒ x 1 = 4 , x 2 = 2
Заметим, что оба корня больше единицы. Это соответствует условию. В результате начальное уравнение обладает двумя решениями:
x 1 = 4 и x 2 = 2
Ответ: x 1 = 4 , x 2 = 2
Найти корни уравнения:
Здесь требуется возвести в квадрат обе части уравнения:
( 3 x – 1 ) 2 = ( x + 5 ) 2
9 x 2 – 6 x + 1 = x 2 + 10 x + 25
8 x 2 – 16 x – 24 = 0
Заметим, что получившееся равенство можно сократить на число 8:
Используя теорему Виета, определим корни уравнения. Предположим, что x 1 и x 2 являются в данном случае решениями, тогда:
x 1 + x 2 = 2 , а x 1 · x 2 = – 3 ⇒ x 1 = 3 и x 2 = – 1 . .
Ответ: x 1 = 3 , x 2 = – 1
Нужно решить уравнение:
| x + 1 | + | x – 5 | = 20
Воспользуемся методом интервалов. Определим х , при которых модули принимают нулевые значения:
x + 1 = 0 ⇒ x = – 1 ; x – 5 = 0 ⇒ x = 5
С помощью данных точек координатная прямая будет поделена на три интервала:
Далее необходимо решить уравнение в каждом случае:
Корень соответствует определенному ранее промежутку.
Этот промежуток не имеет корней.
Этот корень соответствует определенному ранее интервалу.
Ответ: x 1 = – 8 , x 2 = 12
3 x + 1 = 1 – 2 x ⇔ 3 x + 3 = 1 – 2 x 3 x + 3 = 2 x – 1 ⇔ 5 x = – 2 x = – 4 ⇔ x = – 2 5 x = – 4 .
Ответ: x = – 2 5 , x = – 4
Найти корни уравнения:
2 x – 9 = 3 – x ⇔ 3 – x ≥ 0 2 x – 9 = 3 – x 2 x – 9 = x – 3
x ≤ 3 3 x = 12 x = 6 ⇔ x ≤ 3 x = 4 x = 6 ⇔ x ∈ ∅ .
Найти корни уравнения:
– 2 x + 4 = 3 – 4 x ⇔ 2 x + 8 = 4 x – 3 ⇔ ;
4 x – 3 ≥ 0 2 x + 8 = 4 x – 3 2 x + 8 = 3 – 4 x ⇔ x ≥ 3 4 x = 11 2 x = – 5 6 ⇔ x = 11 2 .
Найти корни уравнения:
2 x 2 – 15 = x ⇔ x ≥ 0 2 x 2 – x – 15 = 0 1 2 x 2 + x – 15 = 0 2
Найдем корни квадратных уравнений:
Заметим, что они обладают идентичным дискриминантом:
D = 1 + 4 · 2 · 15 = 121 = 11 2 .
1 : x 1 , 2 = 1 ± 11 4 ⇔ x = 3 x = – 5 2
2 : x 1 , 2 = – 1 ± 11 4 ⇔ x = – 3 x = 5 2
Таким образом, начальное уравнение можно записать в виде системы:
2 x 2 – 15 = x ⇔ x ≥ 0 x = 3 x = – 5 2 x = – 3 x = 5 2 ⇔ x = 3 x = 5 2
Найти корни уравнения:
x + 2 – 3 x – 1 + 4 – x = 3
x + 2 – 3 x – 1 + 4 – x = 3 x + 2 = 0 ⇒ x = – 2 3 x – 1 = 0 ⇒ x = 1 3 4 – x = 0 ⇒ x = 4
– x + 2 + 3 x – 1 + 4 – x = 3
x = 2 > – 2 ⇒ — этот корень является посторонним.
x + 2 + 3 x – 1 + 4 – x = 3 ⇔
3 x = – 2 ⇔ x = – 2 3 ∈ – 2 ; 1 3 этот корень удовлетворяет условиям.
x + 2 – 3 x – 1 + 4 – x = 3 ⇔ – 3 x = – 4 ⇔ x = 4 3 ∈ 1 3 ; 4 этот корень удовлетворяет условиям.
x + 2 – 3 x – 1 – 4 – x = 3 ⇔ x = 4 ⇔ x = – 4 < 4 — корень посторонний
Ответ: – 2 3 ; 4 3 .
Найти корни уравнения:
3 x – 5 + 3 + 2 x = 2 x + 1
3 x – 5 + 3 + 2 x = 2 x + 1 ⇔ 3 x – 5 + 3 + 2 x – 2 x + 1 = 0 .
3 x – 5 = 0 ⇒ x = 5 3 3 + 2 x = 0 ⇒ x = – 3 2 x + 1 = 0 ⇒ x = – 1
– 3 x – 5 – 3 + 2 x + 2 x + 1 = 0 ⇔
– 3 x = – 4 ⇔ x = 4 3 > – 3 2 ⇒ — корень является посторонним
– 3 x – 5 + 3 + 2 x + 2 x + 1 = 0 ⇔
– 3 x – 5 + 3 + 2 x – 2 x + 1 = 0 ⇔
– 3 x = – 6 ⇔ x = 2 > 5 3 ⇒ — корень является посторонним
3 x – 5 + 3 + 2 x – 2 x + 1 = 0 ⇔
В результате на рассмотренных интервалах графика координатной прямой отсутствуют корни. В таком случае уравнение не имеет решений.
Модуль числа
Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная  Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.
Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем. И эту картину мы наблюдаем на протяжении многих лет.
Поэтому осваивайте тему «Уравнения и неравенства с модулем» по нашим статьям и на наших занятиях! Вы сумеете обойти множество конкурентов на ЕГЭ, олимпиадах и вступительных экзаменах.
Модуль числа называют ещё абсолютной величиной этого числа. Попросту говоря, при взятии модуля нужно отбросить от числа его знак. В записи положительного числа и так нет. никакого знака, поэтому модуль положительного числа равен ему самому. Например, Модуль нуля равен нулю. А модуль отрицательного числа равен противоположному ему положительному
(без знака!). Например,

Обратите внимание: модуль числа всегда неотрицателен:
Определение модуля
От большинства известных из школы определений оно отличается лишь одним: в нём есть выбор. Есть условие. И в зависимости от этого условия мы раскрываем модуль либо так, либо иначе.
Так же, как в информатике — в разветвляющихся алгоритмах с применением условных операторов. Как, вообще-то, и в жизни: сдал ЕГЭ на минимальный балл — можешь подавать документы в ВУЗ. Не сдал на минимальный балл — можешь идти в армию 
Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению. Например,
В некоторых случаях модуль раскрывается однозначно. Например, так как выражение под знаком модуля неотрицательно при любых x и y. Или: так так как выражение под модулем неположительно при любых z.
Геометрическая интерпретация модуля
Нарисуем числовую прямую. Модуль числа — это расстояние от нуля до данного числа. Например, То есть расстояние от точки −5 до нуля равно 5.
Эта геометрическая интерпретация очень полезна для решения уравнений и неравенств с модулем.
Рассмотрим простейшее уравнение . Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и −3. Значит, у уравнения есть два решения: x = 3 и x = −3.
Вообще, если имеются два числа a и b, то равно расстоянию между ними на числовой прямой.
(В связи с этим нередко встречается обозначение длины отрезка AB, то есть расстояния от точки A до точки B.)

Ясно, что (расстояние от точки a до точки b равно расстоянию от точки b до точки a).

Решим уравнение . Эту запись можно прочитать так: расстояние от точки x до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Мы видим, что наше уравнение имеет два решения: −1 и 7. Мы решили его самым простым способом — без использования определения модуля.

Перейдём к неравенствам. Решим неравенство .
Эту запись можно прочитать так: «расстояние от точки x до точки −7 меньше четырёх». Отмечаем на числовой прямой точки, удовлетворяющие этому условию.

Ответ: (-11; -3).
Другой пример. Решим неравенство |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ:

График функции
Этот график надо знать обязательно. Для имеем y = x. Для имеем y = −x. В результате получаем:
С помощью этого графика также можно решать уравнения и неравенства.
Корень из квадрата
Нередко в задачах ЕГЭ требуется вычислить , где – некоторое число или выражение. Не забывайте, что
Действительно, по определению арифметического квадратного корня — это такое неотрицательное число, квадрат которого равен . Оно равно при и при , т. е. как раз .
Примеры заданий ЕГЭ
1. Найдите значение выражения при .
Заметим, что при . Следовательно, значение нашего выражения равно: .
2. Найдите значение выражения при .

В следующей статье мы рассмотрим более сложные уравнения и неравенства с модулем.
Модуль
В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа. Разберемся, откуда модуль взялся, какими свойствами обладает. Научимся решать уравнения и неравенства с модулем.
«Величина» числа
Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.
Геометрический смысл
Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.
Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.
Количественный смысл
Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .
Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .
Понятие величины
Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.
Модуль числа
Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.
Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .
Допустим, мы хотим найти модуль какого-то числа a . Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно 0 , то модулем a и является само a . Если же a меньше 0 , то результатом модуля будет − a .
∣ 5 ∣ = 5 ∣ 0 ∣ = 0 ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2
Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» − 1 0 0 больше 5 0 , а − 1 0 равно 1 0 . И действительно:
∣ − 1 0 0 ∣ = 1 0 0 ∣ − 1 0 ∣ = 1 0 ∣ 5 0 ∣ = 5 0 ∣ − 1 0 0 ∣ > ∣ 5 0 ∣ ∣ 1 0 ∣ = 1 0 ∣ − 1 0 ∣ = ∣ 1 0 ∣
Положение знака нестрогого неравенства в определении модуля не имеет значения:
Обозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .
Пусть x > 0 . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .
Пусть x = 0 . По классическому определению ∣ 0 ∣ = 0 . А вот во втором определении 0 попадает уже под второе условие, то есть ∣ 0 ∣ ′ = − 0 = 0 . Опять имеем ∣ 0 ∣ = ∣ 0 ∣ ′ .
Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■
Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: − 1 0 ≤ x ≤ 0 , то можно сразу сказать, что ∣ x ∣ = − x , даже несмотря на то, что для x = 0 так выражаться будет некорректно, ведь ∣ 0 ∣ = 0 , а не − 0 .
Свойства модуля
У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее. Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел x и y .
Очевидные свойства
Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.





