Урок математики по теме “Уменьшаемое, вычитаемое, разность”. 1-й класс
– Громко прозвенел звонок,
Он позвал вас на урок.
Мы будем примеры, задачи решать,
Выводы делать и рассуждать!
Ребята, сегодня у нас математики пройдет в нестандартной обстановке. На уроке вы должны быть внимательными, ответственными и активными. Покажите, как вы научились добывать знания и применять их.
2. Актуализация знаний и пробное учебное действие
1. «Потерялось число» (СЛАЙД 2)
– Что на слайде? (Числа)
– Как числа записаны? (По порядку при счете)
– Что заметили? (нет числа 7)
1 2 3 4 5 6 8 9 10
– Между какими числами стоит 7? (Между числами 6 и 
– За каким числом стоит число 7? (За числом 6)
– Перед каким числом стоит число 7? (Перед числом 
Оцените себя сигнальными карточками «+» и «-» Кто знал ответы на все вопросы поднимет карточку «+», а кто только на некоторые «-»
2. Самоопределение к деятельности. (СЛАЙД 3)
– Как рассказ называется? (задача)
– Сколько мотоциклов? (три) Маша, поставь на доску три треугольника.
– Сколько машинок? (четыре) Дима, поставь на доску четыре четырёхугольника.
– Какой вопрос будет у задачи? (сколько всего игрушек)
– Какое выражение выберем для решения задачи? (3+4=7)
- 7 – 1 = 6
- 5 + 2 = 7
- 3 + 4 = 7
- 5 – 2 = 3
– Прочитайте это выражение, используя знание компонентов действия сложения.
Оля: Первое слагаемое 4, второе слагаемое 3, значение суммы 7.
Миша: Сумма чисел 4 и 3 равна 7.
Оцените себя сигнальными карточками «+» и «-»
– Составьте задачу по рисунку: (СЛАЙД 4)
– Сколько всего шариков? (8) Рома, поставь на доску 8 кружочков.
– Что случилось? (шарик лопнул или улетел) Коля, убери один шарик.
– Какой вопрос будет у задачи? (сколько шариков осталось)
- 7 – 1 = 6
- 5 + 2 = 7
- 3 + 4 = 7
- 5 – 2 = 3
– Какое выражение выберем для решения задачи? (7-1=6)
– Как вы назовёте число 7? 1? 6?
– Можно ли его прочитать это выражение, используя термины, как в предыдущем? (нет) – Почему? (пример на вычитание) В выражении записан знак «минус», а в сумме используется «плюс».
Это выражение нельзя прочитать так, как первое.
3. Целеполагание и построение проекта выхода из затруднения
1. Целеполагание.
– Кто хочет узнать ответ на поставленный вопрос?
– Какая тема нашего урока?
Оля: Название компонентов действия вычитания.
– Это будет урок повторения или открытия новых знаний?
– А для чего нам нужны эти новые знания?
Саша: Чтобы грамотно говорить и хорошо считать.
– А в будущем, чтобы научиться решать уравнения и задачи. Значит, эти знания вам будут необходимы для дальнейшего обучения. Поэтому, какую цель поставим себе на уроке?
Влад: Запомнить названия чисел при вычитании.
Милена: Научиться по-новому читать выражения на вычитание.
– Верно, тема нашего урока название чисел при вычитании (СЛАЙД 5)
4. Выявление места и причины затруднения
– Почему не получилось? (Выявление причины затруднения.)
Миша: Мы не знаем, как называются числа при вычитании.
София: Мы не знаем компонентов действия вычитания.
– На какой вопрос нам предстоит ответить?
Саша: Мы должны узнать, как называются компоненты при вычитании.
1. Построение проекта выхода из проблемной ситуации.
(СЛАЙД 6)
– Перед вами пирожные. Сколько их? (7)
– Что произошло с количеством пирожных?
Катя: Оно уменьшилось.
– А что произошло с числом 7?
Саша: Оно тоже уменьшилось.
Работа в парах
– Как же мы будем называть это число при вычитании? У вас на партах лежат карточки с названием чисел (уменьшаемое, вычитаемое, разность, значение разности). Поработайте в паре друг с другом и выберите подходящий компонент для первого числа (проблемная ситуация).
– Не торопитесь, думайте, советуйтесь.
– Если выбрали, положите эту карточку перед ребёнком, сидящим на 1 варианте.
– Давайте вспомним, а что мы сделали с 1 пирожным?
Ярослав: Убрали.
Полина: Вычли.
София: Отняли.
– Подумайте, как можно назвать это число?
– Выберите, посовещавшись, карточку и положите её справа от первой.
– А теперь вы должны подумать и решить, как мы будем называть математическую запись со знаком «минус» и результат этого действия? Закончите выкладывать карточки по порядку.
– Работая в паре, вы сделали свои предположения. Как проверить их правильность?
Рита: Можно спросить у учителя или посмотреть в учебнике.
– Откройте учебник стр.29. Посмотрите в таблицу. Сравните со своей работой.
Проверка (СЛАЙД 7)
Оцените себя сигнальными карточками «+» и «-»
– Какое открытие мы с вами сделали?
Толя: Узнали компоненты действия вычитания.
– Попробуйте, опираясь на новые знания, прочитать выражение.
(СЛАЙД 
София: Уменьшаемое 7, вычитаемое 4, значение разности равно 6.
Захар: Разность чисел 7 и 1 равна 6.
Итак: В примере на вычитание, какое число из трёх самое большое? (Первое)
– Как вы думаете, почему?
(Дети выясняют, что это целое, из которого можно взять часть)
– Что происходит с первым самым большим числом при вычитании? (Оно уменьшается).
– Что происходит со вторым числом? (Его вычитают).
– А третье число (сообщает учитель) показывает разницу между первым числом и вторым.
– Вопрос “на сколько” задают при сравнении, чтобы найти разницу.
– Как же называется третье число? (Выясняется, что это РАЗНОСТЬ).
В ходе «открытия» нового знания на доске появляются названия чисел УМЕНЬШАЕМОЕ, ВЫЧИТАЕМОЕ, РАЗНОСТЬ, а также буквы –
У – В = Р
5. Физминутка
Для начала мы с тобой крутим только головой. (Вращение головой)
Корпусом вращаем тоже, это мы, конечно, сможем. (Повороты вправо и влево)
Напоследок потянулись, вверх и в стороны прогнулись. (Потягивания вверх и в стороны)
От разминки раскраснелись и за парты снова сели. (Сесть на место)
6. Первичное закрепление
– А сейчас нам предстоит научиться пользоваться новыми знаниями. Составьте задачу по иллюстрации. (СЛАЙД 9)

Оля: На ветке сидело 5 снегирей. 2 снегиря улетели. Сколько снегирей осталось?
– Когда снегири улетели, их осталось больше, чем было или меньше?
Паша: Их осталось меньше на 2.
– Что произошло с количеством снегирей на ветке?
Миша: Оно уменьшилось.
– Как узнать, сколько снегирей осталось?
Алина: Надо от 5 отнять 2 и получится 3.
– Прочитайте получившееся выражение.
Милена: Уменьшаемое 5, вычитаемое 2, значение разности равно 3.
Артём: Разность чисел 5 и 2 равна 3.
7. Включение в систему знаний и повторение. Самостоятельная работа
Учебник стр.29 № 1. (СЛАЙД 10)

Работа у доски: 9 – 4 = 5
Вероника: Уменьшаемое – это первое число, которое мы уменьшаем, поэтому мы записали 9. Вычитаемое – это число, которое мы вычитаем, значит, ставим знак минус и число 4. Мы вычислили результат – это 5. Значит значение разности равно 5.
Гимнастика для глаз.
Глазки вправо, глазки влево, и по кругу проведём.
Быстро – быстро поморгаем и немножечко потрём.
Посмотри на кончик носа и в «межбровье» посмотри.
Круг, квадрат и треугольник по три раза повтори.
Глазки закрываем, медленно вдыхаем.
А на выдохе опять глазки заставляй моргать.
А сейчас расслабились и на места отправились.
– Ребята, а сейчас вы будете работать самостоятельно. Работайте вдумчиво, не отвлекайтесь. Откроем рабочую тетрадь на странице 16 задание № 1. Прочитайте, что нужно сделать. На это странице 3 задания и после выполнения примеров каждый выберает себе задание которое может выполнить: либо задачу, либо геометрический материал.
Взаимопроверка (СЛАЙД 11)
Оцените себя сигнальными карточками «+» и «-».
8. Итог урока. Рефлексия
– Вот и подошёл к концу ещё один урок. Благодаря слаженной работе, взаимовыручке и поддержке друг друга, мы смогла повторить изученный материал и открыть новые знания.
– Какую задачу ставили?
– Какие новые знания получили на уроке?
– Что вам особенно понравилось?
– Что не совсем получилось, какие вы испытали трудности?
– У вас три волшебные буквы сегодняшнего урока. Прикрепите свою букву к моим на доске те, которые вам больше подходят
Уменьшаемое У (Удача Успех Умник Уяснил)
Вычитаемое В (Всезнайка Вдохновлён Всё понял Вдумчиво работал)
Разность Р (Рад помощи Растерялся )
Карточки по математике 1 класс на нахождение уменьшаемого, вычитаемого, разности.
учебно-методический материал по математике (1 класс) на тему
Карточки по математике 1 класс на нахождение уменьшаемого, вычитаемого, разности.
Скачать:
| Вложение | Размер |
|---|---|
| umenshaemoe_vychitaemoe_raznost.docx | 23.08 КБ |
Предварительный просмотр:
- Запиши соседей чисел.
7 4 = 3 1 6 = 7 7 1 = 6
7 2 = 5 4 3 = 7 2 5 = 7
- В книге 8 рассказов. Юра прочитал 3 рассказа. Сколько рассказов осталось прочитать?
- * Запиши любое число, которое меньше разности
7 и 4. ___________
Запиши любое число, которое больше разности
2 и 6 ___________
Запиши любое число, которое меньше разности
5 и 3. ___________
Запиши любое число, которое больше разности
10 и 8. ___________
1. Запиши ответы в строчку.
А. разность чисел 7 и 3.
Б. сумма чисел 3 и 2.
В. число, которое меньше 5 на 4.
Г. увеличь 4 на 4.
Д. уменьши 9 на 7.
Е. на сколько 4 меньше 6.
Ж. на сколько 6 больше 1.
- Вставь пропущенные числа, чтобы записи были верными.
- Запиши 3 примера, у которых сумма равна 8.
- В маршрутном такси ехали 10 человек. На остановке вышли 5 человек, а вошли 3. Сколько человек едет дальше?
А. разность чисел 10 и 5.
Б. сумма чисел 3 и 6.
В. число, которое меньше 8 на 4.
Г. увеличь 6 на 4.
Д. уменьши 9 на 1.
Е. на сколько 5 меньше 8.
Ж. на сколько 6 больше 3.
6+3…..8-4 8-6…1+1 10-3…10-7
- Вставь пропущенные знаки.
- Бабушка собрала 9 кг клубники. Из 6 кг сварили компот. Сколько килограммов клубники осталось?
- Запиши ответы в строчку.
А. найди сумму 3 и 6.
Б. на сколько 7 меньше 8.
В. что прибавили к 2, чтобы получить 10.
Г. первое слагаемое – 3, чему равно второе, если сумма равна 6.
Д. найди сумму 2 и 3.
Е. найди разность 8и 5.
- Подчеркни примеры с ответом 8.
- Вставь подходящее число.
- У Кати 5 леденцов и 3 батончика. Сколько конфет у Кати?
По теме: методические разработки, презентации и конспекты

Урок математики в 1 классе по теме “Уменьшаемое, вычитаемое, разность” по программе “Школа России”
Урок математики по теме “Уменьшаемое, вычитаемое, разность” составлен на основе деятельностного обучения. Соответствует новым стандартам. В ходе групповой работы учащиеся учатся открывать новые знания.
Математика. 1 класс. Урок 43. Уменьшаемое. Вычитаемое. Разность – Презентация
ссылка на источник: http://avtatuzova.ru/news/matematika_1_klass_urok_43_umenshaemoe_vychitaemoe_raznost/2012-11-21-136 Урок 43. Уменьшаемое. Вычитаемое. Разность В презентации от.

Урок математики в 1 классе по теме “Уменьшаемое. вычитаемое, разность”.
Данный урок предназначен для учащихся 1 класса ( ОС” Школа 2100″) Цели урока:1)Помочь детям усвоить счет в пределах 7;название компонентов и результата действия вычитания, взаимосвязь между изменением.

Урок математики в 1 классе по теме “Уменьшаемое.Вычитаемое.Разность.”
Урок математикиКласс 1Тема: “Уменьшаемое. Вычитаемое. Разность”Тип урока: ОНЗ (открытие новых знаний)Цели урока: Познакомится с названиями компонентов при вычитанииПредметные:Знать название компоненто.

Урок математики в 1 классе по теме: “Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей”.
Планируемые результаты:Предметные:учащиеся научатся использовать математическую терминолугию при составлении, чтении и записи математических равенств на вычитаниие, выполнять устно и письменно а.
Конспект урока математики в 1 классе на тему: “Уменьшаемое, вычитаемое, разность”.
На данном уроке проводится знакомство с названиям компонентов при вычитании, составляются и записываются выражения, используются в речи термины “уменьшаемое, вычитаемое, разность”, устно и письм.

Разработка урока по математике в 1 классе по теме “«Уменьшаемое. Вычитаемое. Разность. Закрепление»
На данном уроке поставлены цели:1.Закрепить названия чисел при вычитании (уменьшаемое, вычитаемое, разность) сложении (слагаемые, сумма); использование этих терминов при чтении записей.2. Формирование.
Неизвестное слагаемое — правила нахождения
В школьной программе встречаются уравнения разной сложности. Они могут быть как с одним, так и с несколькими слагаемыми. При этом в них ещё могут присутствовать степени, логарифмы и другие математические операции. Освоить их вполне реально. Главное — постоянно тренироваться и совершенствовать свои навыки по решению уравнений. Сначала перед вами встанет задача, требующая найти неизвестное слагаемое. Затем нужно будет решить несколько примеров. И только потом можно повышать уровень сложности.

Способ найти 1 слагаемое
Разберём в качестве примера решение одного элементарного уравнения. Из чего оно состоит? Как правило, это сумма и два слагаемых, одно из которых известно, другое — нет. Преимущественно неизвестное слагаемое обозначается буквой «икс», прописью x.

Например, уравнение выглядит следующим образом: 3+x=8. Как его решить? Воспользуемся законами элементарной логики. У нас есть сумма двух чисел. Одно из них известно, а второе — нет. То есть для того, чтобы узнать неизвестное, необходимо из суммы вычесть известное слагаемое. Получаем результат: 8−3=5.
Конечно, взрослому человеку с рациональным и логическим мышлением это кажется простым и понятным. А как быть, если необходимо научить ребёнка нахождению слагаемого? Можно объяснить на простых и понятных примерах. Например, задать вопрос: У Димы было 3 рубля, и после того как Петя дал ему денег, у Димы стало 8 рублей. Сколько рублей ему дал Петя?
Самый простой пример — счёты на пальцах. Сначала можно показать ребёнку 3 пальца, а потом 8. После чего попросить его посчитать, сколько пальцев вы добавили. Главное — не пытаться всё объяснить сложными словами. Предложенные примеры буду более эффективными. Однако повторить правило нахождения неизвестного слагаемого не будет лишним. Оно формулируется следующим образом: чтобы найти неизвестное слагаемое, надо известное слагаемое вычесть из суммы.
После того как вы решили уравнение, рекомендуется сделать проверку, чтобы убедиться, что всё сделано правильно. Сложите получившийся результат неизвестного слагаемого с известным слагаемым. Если сумма совпадает с суммой, то решение правильное. В нашем случае проверка: 3+5=8.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Правила нахождения уменьшаемого

При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Уравнения с умножением и делением
После освоения уравнений на сложение и вычитание можно будет переходить к следующему уровню сложности. Это уравнения с умножением и делением.
Компоненты уравнения с умножением:
Например, 3*x=6. Здесь 3 и x — множители, а 6 — произведение. Так, умножая одно число на другое, в результате получается произведение. То есть, если одно из этих чисел неизвестно, необходимо разделить произведение на известный множитель. В этом случае действует такое же правило, как и при сложении. При перестановке мест множителей произведение не меняется.
Компоненты уравнения с делением:

Возьмём простейший пример 8: x=4. Здесь делимое 8, делитель x, а частное — 4. Для поиска неизвестного делителя необходимо разделить делимое на частное. Для упрощения понимания можно представить это уравнение в виде элементарной задачи. В классе 8 учеников, которые разделились на группы по 4 человека. Вопрос: сколько получилось групп?
Есть ещё один вариант — с поиском делимого. Например, уравнение x_2=5. Для поиска делимого необходимо частное умножить на делитель. Пример задачи: 2 мальчика заработали по 5 долларов каждый, какова общая сумма их заработка?
Между делением и умножением похожая взаимосвязь, как между сложением и вычитанием. То есть для того, чтобы лучше решать уравнения с умножением, необходимо также решать их с делением и наоборот. Этот подход в тренировке навыка решения уравнений ускоряет мыслительный процесс.
Поиск неизвестных компонентов уравнения не такой уж и сложный. Главное — начинать с простого и регулярно решать уравнения с одним неизвестным. И тогда для вас будут открыты более сложные задачи — с двумя и более неизвестными.
Поиск вычитаемого, уменьшаемого и разности для первоклассников
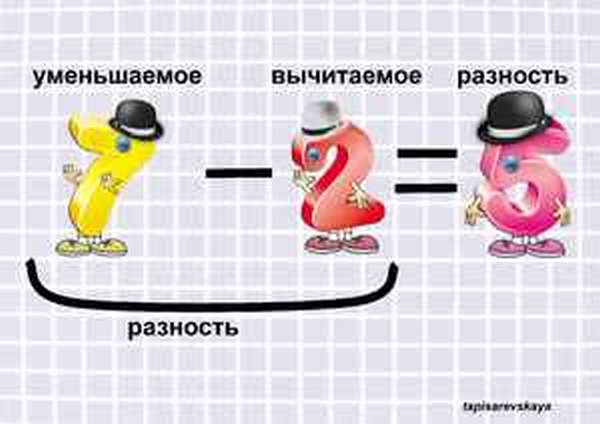
Длинная дорога в мир знаний начинается с первых примеров, простых уравнений и задач. В нашей статье мы рассмотрим уравнение вычитания, которое, как известно, состоит из трёх частей: уменьшаемое, вычитаемое, разность.
Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.
- Как найти неизвестные
- Как найти разность
- Правило поиска уменьшаемого
- Как найти вычитаемое
Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.
Это интересно: разрядные слагаемые что это?
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.
Как найти неизвестные

Мы познакомились с тремя братьями:
- Уменьшаемым
- Вычитаемым
- Разностью.
Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.
Это интересно: что такое хорда окружности в геометрии, определение и свойства.
Как найти разность
Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.
Правило поиска уменьшаемого
Теперь узнаем, что делать, если потерялось Уменьшаемое.

- Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
- Теперь, чтобы быть уверенными, сделаем небольшую проверку — подставим все на свои места и вычислим разность. Итак, 10 -4= 6. Разность совпадает, а значит мы сделали все верно. У нас было 10 яблок, мы съели 4, осталось 6.
Как найти вычитаемое
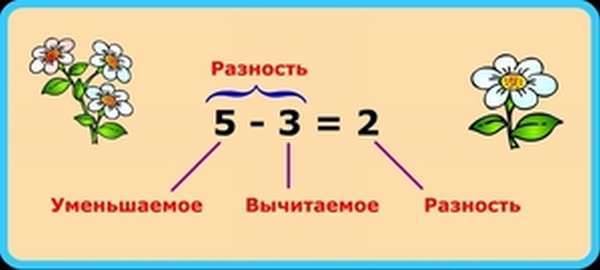
Рассмотрим, что делать, если потерялось Вычитаемое. Представим, что мы купили 7 яблок, принесли домой и ушли гулять, а когда вернулись — осталось всего 4. Вычитаемым в этом случае будет то количество яблок, которое кто-то съел в наше отсутствие. Давайте обозначим это число в виде буквы Y. Получится уравнение 7-Y=4. Чтобы найти неизвестное вычитаемое, надо знать простое правило и сделать следующее — из Уменьшаемого отнять Разность, то есть 7 -4= 3. Наше неизвестное значение отыскалось, это 3. Ура! Теперь мы знаем, сколько было съедено.
На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.
Правила очень простые, но, чтобы быть уверенными и ничего не забыть, можно поступить так — самому для себя придумать лёгкий и понятный пример на вычитание и, решая другие примеры, отыскивать неизвестные значения, просто подставляя цифры и легко находить правильный ответ. Например, 5−3= 2. Мы уже знаем, как найти и Уменьшаемое 5, и Вычитаемое 3, поэтому решая более сложное уравнение, скажем, 25-Х= 13, мы можем вспомнить наш простой пример и понять, что, чтобы найти неизвестное Вычитаемое, нужно лишь отнять от 25 число 13, то есть 25 -13= 12.
Ну вот, теперь мы познакомились с вычитанием, его главными участниками.
Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!
Поиск вычитаемого, уменьшаемого и разности для первоклассников
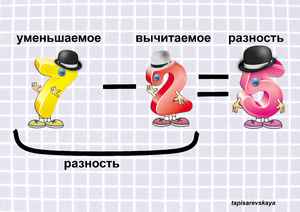
Длинная дорога в мир знаний начинается с первых примеров, простых уравнений и задач. В нашей статье мы рассмотрим уравнение вычитания, которое, как известно, состоит из трёх частей: уменьшаемое, вычитаемое, разность.
Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.
Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.
Как найти неизвестные

Мы познакомились с тремя братьями:
- Уменьшаемым
- Вычитаемым
- Разностью.
Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.
Как найти разность
Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.
Правило поиска уменьшаемого
Теперь узнаем, что делать, если потерялось Уменьшаемое.

- Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
- Теперь, чтобы быть уверенными, сделаем небольшую проверку — подставим все на свои места и вычислим разность. Итак, 10 -4= 6. Разность совпадает, а значит мы сделали все верно. У нас было 10 яблок, мы съели 4, осталось 6.
Как найти вычитаемое
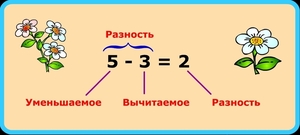
Рассмотрим, что делать, если потерялось Вычитаемое. Представим, что мы купили 7 яблок, принесли домой и ушли гулять, а когда вернулись — осталось всего 4. Вычитаемым в этом случае будет то количество яблок, которое кто-то съел в наше отсутствие. Давайте обозначим это число в виде буквы Y. Получится уравнение 7-Y=4. Чтобы найти неизвестное вычитаемое, надо знать простое правило и сделать следующее — из Уменьшаемого отнять Разность, то есть 7 -4= 3. Наше неизвестное значение отыскалось, это 3. Ура! Теперь мы знаем, сколько было съедено.
На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.
Правила очень простые, но, чтобы быть уверенными и ничего не забыть, можно поступить так — самому для себя придумать лёгкий и понятный пример на вычитание и, решая другие примеры, отыскивать неизвестные значения, просто подставляя цифры и легко находить правильный ответ. Например, 5−3= 2. Мы уже знаем, как найти и Уменьшаемое 5, и Вычитаемое 3, поэтому решая более сложное уравнение, скажем, 25-Х= 13, мы можем вспомнить наш простой пример и понять, что, чтобы найти неизвестное Вычитаемое, нужно лишь отнять от 25 число 13, то есть 25 -13= 12.
Ну вот, теперь мы познакомились с вычитанием, его главными участниками.
Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!
Неизвестное слагаемое – правила нахождения
В школьной программе встречаются уравнения разной сложности. Они могут быть как с одним, так и с несколькими слагаемыми. При этом в них ещё могут присутствовать степени, логарифмы и другие математические операции. Освоить их вполне реально. Главное — постоянно тренироваться и совершенствовать свои навыки по решению уравнений. Сначала перед вами встанет задача, требующая найти неизвестное слагаемое. Затем нужно будет решить несколько примеров. И только потом можно повышать уровень сложности.
- Способ найти 1 слагаемое
- Другие методы
- Правила нахождения уменьшаемого
- Поиск вычитаемого
- Общие правила
- Уравнения с умножением и делением

Способ найти 1 слагаемое
Разберём в качестве примера решение одного элементарного уравнения. Из чего оно состоит? Как правило, это сумма и два слагаемых, одно из которых известно, другое — нет. Преимущественно неизвестное слагаемое обозначается буквой «икс», прописью x.

Например, уравнение выглядит следующим образом: 3+x=8. Как его решить? Воспользуемся законами элементарной логики. У нас есть сумма двух чисел. Одно из них известно, а второе — нет. То есть для того, чтобы узнать неизвестное, необходимо из суммы вычесть известное слагаемое. Получаем результат: 8−3=5.
Конечно, взрослому человеку с рациональным и логическим мышлением это кажется простым и понятным. А как быть, если необходимо научить ребёнка нахождению слагаемого? Можно объяснить на простых и понятных примерах. Например, задать вопрос: У Димы было 3 рубля, и после того как Петя дал ему денег, у Димы стало 8 рублей. Сколько рублей ему дал Петя?
Самый простой пример — счёты на пальцах. Сначала можно показать ребёнку 3 пальца, а потом 8. После чего попросить его посчитать, сколько пальцев вы добавили. Главное — не пытаться всё объяснить сложными словами. Предложенные примеры буду более эффективными. Однако повторить правило нахождения неизвестного слагаемого не будет лишним. Оно формулируется следующим образом: чтобы найти неизвестное слагаемое, надо известное слагаемое вычесть из суммы.
После того как вы решили уравнение, рекомендуется сделать проверку, чтобы убедиться, что всё сделано правильно. Сложите получившийся результат неизвестного слагаемого с известным слагаемым. Если сумма совпадает с суммой, то решение правильное. В нашем случае проверка: 3+5=8.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Правила нахождения уменьшаемого
При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Уравнения с умножением и делением
После освоения уравнений на сложение и вычитание можно будет переходить к следующему уровню сложности. Это уравнения с умножением и делением.
Компоненты уравнения с умножением:
- Два множителя.
- Произведение.
Например, 3*x=6. Здесь 3 и x — множители, а 6 — произведение. Так, умножая одно число на другое, в результате получается произведение. То есть, если одно из этих чисел неизвестно, необходимо разделить произведение на известный множитель. В этом случае действует такое же правило, как и при сложении. При перестановке мест множителей произведение не меняется.
Компоненты уравнения с делением:

Возьмём простейший пример 8: x=4. Здесь делимое 8, делитель x, а частное — 4. Для поиска неизвестного делителя необходимо разделить делимое на частное. Для упрощения понимания можно представить это уравнение в виде элементарной задачи. В классе 8 учеников, которые разделились на группы по 4 человека. Вопрос: сколько получилось групп?
Есть ещё один вариант — с поиском делимого. Например, уравнение x_2=5. Для поиска делимого необходимо частное умножить на делитель. Пример задачи: 2 мальчика заработали по 5 долларов каждый, какова общая сумма их заработка?
Между делением и умножением похожая взаимосвязь, как между сложением и вычитанием. То есть для того, чтобы лучше решать уравнения с умножением, необходимо также решать их с делением и наоборот. Этот подход в тренировке навыка решения уравнений ускоряет мыслительный процесс.
Поиск неизвестных компонентов уравнения не такой уж и сложный. Главное — начинать с простого и регулярно решать уравнения с одним неизвестным. И тогда для вас будут открыты более сложные задачи — с двумя и более неизвестными.





