Перпендикулярность в пространстве
Мы уже сталкивались с перпендикулярными прямыми в планиметрии. В стереометрии это понятие расширяется.
План урока:
Перпендикулярность прямых
Напомним, что планиметрии две прямые перпендикулярны, если угол между ними – прямой (то есть его величина составляет 90°).
Однако в стереометрии угол измеряется и между скрещивающимися двумя прямыми в пространстве, у которых общих точек нет. Если он составляет 90°, то прямые также именуются перпендикулярными.
Как же проверить, перпендикулярны ли скрещивающиеся прямые или нет? Для этого может быть использована специальная теорема, которую можно считать признаком перпендикулярности прямых.
Действительно, пусть есть прямые m, n и p, причем р||n и m⊥n. Требуется показать, что также m⊥p. Для этого выберем в пространстве какую-нибудь точку К и проведем через нее две такие прямые m’ и n’, что m’||m и n’||n:
По определению угла между прямыми из того факта, что m⊥n, вытекает, что и m’⊥n’. Так как p||n и n||n’, то в силу транзитивности параллельности, можно сделать вывод, что и р||n’. Но тогда угол между m’ и n’ одновременно является углом между m и p. А разm’⊥n’, то и m⊥p, ч. т. д.
Проиллюстрируем это правило на примере простого кубика:
Ребра ВС и AD параллельны как стороны квадрата АВСD. В свою очередь ВС⊥СG. Тогда по доказанной теореме можно утверждать, что и AD⊥CG.
Перпендикулярность прямой и плоскости
Из реальной жизни мы знаем, что палку в землю можно вставить так, что она будет стоять строго вертикально. В таких случаях говорят, что палка располагается перпендикулярно земле. Также гвоздь, «ровно» забитый в стену, оказывается перпендикулярным стене. Колонны, которые архитекторы используют при строительстве, также перпендикулярны плоскости пола в этих зданиях.
По аналогии и в геометрии прямая может быть перпендикулярна плоскости. На рисунке такая ситуация будет выглядеть так:
Сформулируем строгое определение:
Так, на следующем рисунке перпендикулярны прямая m и плоскость α. Это значит, что m перпендикулярна каждой прямым, находящимся в α:
Ясно, что прямая m, перпендикулярная плоскости α, должна пересекать ее. Действительно, если бы это было не так, то m либо полностью лежала бы в α, либо была бы ей параллельна. В обоих случаях в α можно было бы построить прямую n, параллельную m. В этом случае m и n уже не были бы перпендикулярны, а значит, что m уже не будет перпендикулярна к α.
Сформулируем две теоремы, связанные с перпендикулярностью прямой и плоскости.
Действительно, пусть есть прямые m и n, и m||n. Также есть плоскость α, и α⊥m. Проведем в α какую-нибудь прямую р:
По определению перпендикулярности (опр. 2) ясно, что m⊥p. Тогда по теор. 1 и n⊥p, ведь m||n. Прямая р была выбрана произвольно, поэтому получается, что n перпендикулярно любой произвольной прямой в α. Это как раз и значит, что n⊥α.
Теперь перейдем ко второй теореме, которая по сути обратна первой:
Для доказательства выберем на n точку К, не находящуюся в плоскости α. Через нее можно построить прямую р, параллельную m. Нам надо показать, что р и n – это одна и та же прямая. Пусть это не так, тогда р будет перпендикулярна α по теор. 2. Если n и р – различные прямые, то они должны пересекать α в разных точках, которые мы обозначим буквами Н и Т соответственно:
Прямая ТН будет перпендикулярна и n, и р. Тогда в ∆ТНК есть два прямых угла, ∠Н и∠Т, что невозможно. Значит, на самом деле прямые n и p совпадают. Так как p||m, то и n||m, ч. т. д.
Признак перпендикулярности прямой и плоскости
Заметим,что проверять перпендикулярность прямой и плоскости с помощью определения неудобно, ведь в любой плоскости находится бесконечно большое количество прямых. Поэтому на практике используется более простой признак перпендикулярности прямой и плоскости:
Доказательство. Пусть есть прямые m, n и р, причем m⊥n и m⊥p. При этом n и р пересекаются в какой-нибудь точке О, и через них проходит плоскость α.Надо продемонстрировать, что m также будет перпендикулярна и любой произвольной прямой k, принадлежащей α:
Если k||nили k||р, то k⊥m по теор. 1. Тогда надо рассмотреть случай, когда k пересекается с n и р. Проведем через О прямую k’, параллельную k.
Далее на прямой m отложим точки А и В так, чтобы ОА = АВ. Также проведем прямую s, пересекающую р, n, k’ в точках Р, L и Q соответственно:
В результате такого построения прямые n и р оказались серединными перпендикулярами для отрезка АВ. Тогда по свойству серединного перпендикуляра мы можем прийти к выводу, что
Теперь мы можем сравнить ∆АРQ и ∆BPQ, которые также оказываются равными:
Отсюда вытекает, что отрезки АQ и BQ одинаковы, поэтому ∆АВQ – равнобедренный. Теперь заметим, что в ∆АВQ отрезок OQ представляет собой медиану, ведь О – середина АВ. Но медиана в равнобедренном треугольнике – это ещё и высота, поэтому АВ⊥OQ. Это как раз и значит, что k’⊥m. Наконец, отсюда по теор. 1 выходит, что и k⊥m, ч. т. д.
Надо также рассмотреть и второй случай, когда изначально m НЕ проходит через О. В таком случае мы можем провести через О прямую m’, чтобы m’||m:
В этом случае по аналогии с предыдущим доказательством получаем, что m’⊥k. Тогда по теор. 1 и m⊥k, ч. т. д.
Покажем, как можно применить доказанный признак. Снова рассмотрим куб:
Докажем, что, например, ребро DH перпендикулярно грани АВСD. Действительно,DH⊥AD и DH⊥CD. Значит, в плоскости АВСD есть две пересекающиеся прямые (это AD и CD), каждая из которых перпендикулярна DH. По доказанному признаку (теор. 4) этого достаточно для того, чтобы DH⊥ABCD. Аналогично можно показать, что ребра BF, AE, СG также перпендикулярны АВСD.
Докажем ещё несколько важных и вместе с тем очевидных теорем.
Действительно, пусть есть прямая m и точка K. Здесь мы рассмотрим случай, когда K не находится на m. Тогда через m и K можно построить единственную плоскость α:
Дальше выполним следующие построения:
1) Проведем в плоскости α через К прямую n, такую, что n⊥m. Она пересечет m в какой-то точке Т.
2) Построим через m плоскость β, не совпадающую с α. То есть m окажется границей между α и β.
3) Через точку Т уже в плоскости β построим прямую р так, чтобы р⊥m.
4) Построим плоскость γ, проходящую пересекающиеся прямые р и n (эта плоскость будет единственной).
В итоге мы получили плоскость γ, в которой располагаются две прямые, р и n, каждая из которых перпендикулярна m. Тогда и вся плоскость γ будет перпендикулярна прямой m по теор. 4. То есть γ удовлетворяет условию теоремы.
В случае, когда точка К находится непосредственно на прямой m, плоскости α и β будут просто двумя различными плоскостями, проходящими через m. В каждой из них через К можно будет построить перпендикуляры к m, которые и будут играть роль прямых pи n.
Осталось убедиться, что γ – единственная плоскость, удовлетворяющая условию теоремы. В самом деле, пусть через некоторую точку К можно построить хотя бы две несовпадающие плоскости, перпендикулярные прямой m:
Обозначим буквами Т и Р точки, где m пересекает эти две плоскости. Тогда по опр. 2 получится, что РК⊥m и KT⊥m. Теперь рассмотрим ∆KPT. У него сразу два прямых угла – это ∠Р и ∠Т. Треугольник с двумя прямыми углами существовать не может, значит, на самом деле через K нельзя провести две плоскости, перпендикулярных m.
Прямым следствием из только что доказанной теоремы является следующее утверждение:
Действительно, пусть существуют такие плоскости α и β и прямая m, что m⊥α, m⊥β. Предположим, что α и β пересекаются по какой-нибудь прямой n. Тогда получается, что через каждую точку, принадлежащую n, проведены сразу 2 плоскости, перпендикулярные m, а это невозможно по теор. 5. Значит, α и β не пересекаются, то есть они параллельны.
Следующее утверждение часто называют теоремой о прямой, перпендикулярной плоскости:
Возьмем произвольные плоскость α и точку К. Далее в α выберем какую-нибудь прямую m. Мы можем провести через К такую плоскость β, что β⊥m (по теор. 5):
Прямую, по которой пересекутся α и β, обозначим буквой n. Теперь мы можем в плоскости β опустить перпендикуляр из К на n. Этот перпендикуляр обозначим буквой р.
Получается, что р⊥n,но также и р⊥m (ведь m⊥β, а р находится в β). Тогда по признаку перпендикулярности (теор. 4) получаем, что р⊥α, то есть р – это как раз искомая прямая.
Осталось показать, что р – единственная такая прямая. Действительно, пусть через К построили две прямых, каждая из которых перпендикулярна α. Тогда, по теореме 3, они окажутся параллельными. Но при этом у них будет общая точка K, а параллельные прямые общих точек не имеют. Поэтому р – единственная прямая, удовлетворяющая условию теоремы.
Задачи на перпендикулярность
Прежде, чем смотреть решение задач, постарайтесь решить их самостоятельно.
Задание. Ребра ВС и AD в тетраэдре АВСD перпендикулярны. M и N – это середины ребер АВ и АС. Докажите, что MN⊥AD.
Решение.MN по определению оказывается средней линией в ∆АВС. Это значит, что MN||ВС. Тогда, по теор. 1, можно утверждать, что и АD⊥MN, ч. т. д.
Задание. Диагонали квадрата, чья сторона имеет длина а, пересекаются в точке О. Через О проведена прямая ОК, перпендикулярная плоскости квадрата, причем отрезок ОК имеет длину b. Найдите расстояние от какой-нибудь вершины квадрата до точки К.
Обозначим вершины квадрата буквами А, В, С и D. Найдем длину его диагонали, например, АС. Для этого используем теорему Пифагору и прямоугольный ∆АСD:
Точка пересечения диагоналей квадрата одновременно является серединой каждой диагонали, то есть отрезок ОС вдвое короче АС:
Теперь заметим, что если ОК перпендикулярна плоскости квадрата, то также ОК⊥ОС (опр. 2). Значит, ∆КОС – прямоугольный, и для него справедлива теорема Пифагора:
Аналогично можно показать, что расстояние и до других вершин вычисляется по такой же формуле.
Задание. В кубе найдите угол между прямыми АС и DH:
Решение. Заметим, что DH⊥АD и DH⊥CD, при этом AD и CD находятся в плоскости грани АВСD. Тогда по теор. 4 получаем, что DH перпендикулярна этой грани. В свою очередь из опр. 2 вытекает, что DH перпендикулярна любой прямой, принадлежащей грани, в том числе и АС. То есть угол между этими прямыми составляет 90°.
Задание. Ребро куба имеет длину, равную единице. Какова длина его диагонали FD?
Решение. Предварительно найдем длину диагонали FC (эта диагональ называется не диагональю куба, а диагональю грани ВСGF). Ее можно найти из прямоугольного ∆FCG:
Далее заметим, что СD⊥BC и CD⊥CG, то есть по теор. 4 ребро CD перпендикулярно всей грани BCGF. Это значит, что и ∠FCD– прямой, а ∆FCD – прямоугольный. Применим и к нему теорему Пифагора:
Задание. Какой угол в кубе с единичным ребром образуют диагональ куба и его ребро?
Решение. Используем рисунок предыдущей задачи и полученные в ней результаты. Нам надо найти ∠FDC. Мы уже рассчитали длины всех сторон в ∆FDC:
Тогда ∠FDC легко найти с помощью теоремы косинусов:
Примечание. Несложно показать, что ровно такой же угол диагональ куба образует и со всеми остальными ребрами куба. Также можно показать, что это угол никак не зависит от длины ребра.
Задание. Отрезок PQ и плоскость α параллельны. Через точку P и Q построены прямые, перпендикулярные α. Они пересекают α в точках Р1 и Q1. Докажите, что отрезки PQ и P1Q1 одинаковы.
Решение. По условию РР1⊥α и QQ1⊥α. Тогда по теор. 3 можно утверждать, что РР1||QQ1. Это значит, что отрезки РР1 и QQ1, в том числе и точки Р, Р1, Q, Q1 располагаются в одной плоскости. Тогда РQQ1P1– это плоский четырехугольник.
Заметим, что PQ||P1Q1, ведь если бы они пересекались, то точка их пересечения была бы общей для PQ и α, и тогда PQ и α не были бы параллельны. С учетом того факта, что и РР1||QQ1, получаем, что в четырехугольнике РQQ1P1 противоположные стороны параллельны. То есть он представляет собой параллелограмм.
Получается, что все углы в РQQ1P1 – прямые, то есть это прямоугольник. Из этого вытекает, что PQиP1Q1 – одинаковые отрезки, ч. т. д. Попутно мы также убедились, что также РР1 и QQ1 одинаковы.
Задание. Есть плоскости α и β, параллельные друг другу. Прямая m перпендикулярна α. Верно ли, что также m перпендикулярна и β?
Пусть α и m пересекаются в точке Р. Заметим, что m обязательно должна пересекаться и с β в какой-нибудь точке М. Действительно, m не может полностью принадлежать β, ведь тогда бы точка Р также находилась в β, то есть существовала бы общая точка Р у параллельных плоскостей, что невозможно. Если бы m и β были параллельны, то тогда в β можно провести такую прямую m’, что m’||m. Раз m пересекает α, то и m’ должна пересекаться с α (по теор. 3 из этого урока). Но m’ с α не может пересечься, так как m’ находится в β и потому общих точек с α не имеет. Это противоречие показывает, что m пересекает β в точке, обозначенной нами как М.
Предположим, что утверждение в условии ошибочно и на самом деле β и m не перпендикулярны. Тогда через М можно провести третью плоскость γ, перпендикулярную m (по теор. 5). Проанализируем расположение плоскостей α, β и γ. Раз α⊥m и γ⊥m, то по теор. 6 можно утверждать, что α||γ. По условию α||β. Тогда в силу транзитивности параллельности и β||γ. Но это невозможно, ведь уβ и γ есть общая точка М. Значит, на самом деле β и m всё же перпендикулярны, ч. т. д.
Задание. Прямые AD, АС, АВ попарно параллельны. Известно, что
Найдите длину отрезка CD.
Решение. В задаче есть сразу три прямоугольных треугольника: ∆АВС, ∆АВD и ∆АСD. Для каждого из них можно записать теорему Пифагора, что позволит найти длины отрезков АС, АD и СD. Начнем с ∆АВС:
Теперь можно найти и длину CD c помощью ∆АСD:
Задание. На прямой m отмечена точка М. Через точку M проведены плоскость α и прямая n, причем m⊥α и m⊥n. Докажите, что n обязательно принадлежит α.
Решение. Так как m и n пересекаются, то через них можно построить плоскость β:
Так как у α и β есть общая точка М, то они должны пересекаться по некоторой прямой р. При этом р находится в α, а m⊥α, то m⊥n (по опр. 2). Тогда получается, что в плоскости β через точку M проходят две прямые, n и p, которые перпендикулярны m. Но в одной плоскости через точку прямой можно построить строго один перпендикуляр к ней. То есть n и p совпадают. Это значит, что n, как и p, полностью находится в α, ч. т. д.
Задание. Отрезок АВ не пересекает плоскость α, а отрезок СD принадлежит α. Известно, что отрезки АС и BD перпендикулярны α. Также известны длины:
Какова длина АВ?
Если АС⊥α и BD⊥α, то АС||BD (по теор. 3). Это значит, что через АВ и СD можно провести плоскость, то есть АВСD – плоский четырехугольник. При этом∠С и ∠D прямые (по опр. 2). Построим отдельно этот четырехугольник и проведем некоторые построения:
Опустим из В перпендикуляр ВК на АС. Так как в четырехугольнике СDBK три угла прямые (∠С, ∠D и ∠K), то и четвертый угол также прямой, то есть СDBK – прямоугольник. Это значит, что
В ходе сегодняшнего урока мы узнали о перпендикулярных прямых в пространстве, а также о том, что перпендикулярны могут быть также прямая и плоскость. На основе простейших теорем о перпендикулярности возможно определять длину диагонали в кубе и углы, которые образует его диагональ с ребрами куба.
Признак перпендикулярности прямой и плоскости: теория и практика
Закрепим понятие перпендикулярности прямой и плоскости конспектом урока. Предоставим общее определение, сформулируем и приведём доказательства теоремы и решим несколько задач на закрепление материала.
Из курса геометрии известно: две прямые считаются перпендикулярными, когда они пересекаются под углом 90 о .
Теоретическая часть
Переходя к исследованию характеристик пространственных фигур, будем применять новое понятие.
прямая будет называться перпендикулярной плоскости, когда она перпендикулярна прямой на поверхности, произвольно проходящей через точку пересечения.
Иначе говоря, если отрезок «АВ» перпендикулярен плоскости α, тогда угол пересечения со всяким отрезком, проведённым по данной поверхности через «С» точку прохождения «АВ» через плоскость α, будет 90 о .
Из вышесказанного вытекает теорема о признаке перпендикулярности прямой и плоскости:
в случае если прямая, проведённая через плоскость, будет перпендикулярна двум прямым, проведённым на плоскости через точку пересечения, то она перпендикулярна целой плоскости.
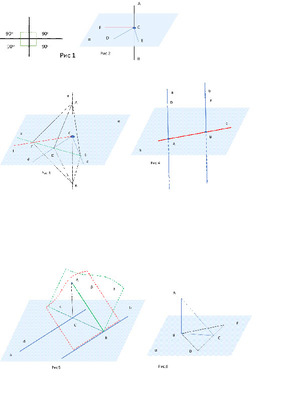
Говоря другими словами, если на рисунке 1 углы ACD и ACE равны 90 о , то и угол ACF тоже будет 90 о . Смотреть рисунок 3.
Доказательство
По условиям теоремы линия «а» проведена перпендикулярно линиям d и e. Иначе говоря, углы ACD и ACE равны 90 о . Приводить доказательства будем, исходя из свойств равенства треугольников. Смотреть рисунок 3.
Через точку C прохождения линии a через плоскость α прочертим линию f в произвольном направлении. Приведём доказательства, что она будет перпендикулярна отрезку AB или угол ACF будет 90 о .
На прямой a отложим отрезки одинаковой длины AC и AB. На поверхности α проведём линию x в произвольном направлении и не проходящую через место пересечения в точке «С». Линия «х» должна пересекать линии e, d и f.
Соединим прямыми точки F, D и E c точками A и B.
Рассмотрим два треугольника ACE и BCE. По условиям построения:
- Имеются две одинаковые стороны AC и BC.
- У них дна общая сторона CE.
- Два равных угла ACE и BCE — по 90 о .
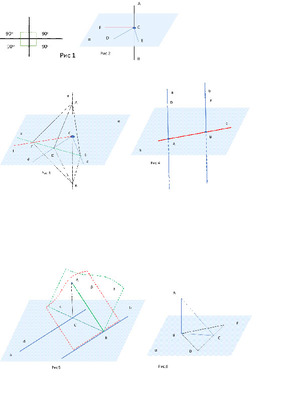
Следовательно, по условиям равенства треугольников, если имеем две равные стороны и одинаковый угол между ними, то эти треугольники равны. Из равенства треугольников следует, что стороны AE и BE равны.
Соответственно доказывается равенство треугольников ACD и BCD, иначе говоря, равенство сторон AD и BD.
Теперь рассмотрим два треугольника AED и BED. Из ранее доказанного равенства треугольников следует, что у этих фигур есть одинаковые стороны AE с BE и AD с BD. Одна сторона ED общая. Из условия равенства треугольников, определённых по трём сторонам, следует, что углы ADE и BDE равны.
Сумма углов ADE и ADF составляет 180 о . Сумма углов BDE и BDF также будет 180 о . Так как углы ADE и BDE равны, то и углы ADF и BDF равны.
Рассмотрим два треугольника ADF и BDF. Они имеют по две равных стороны AD и BD (доказано ранее), DF общую сторону и по равному углу между ними ADF и BDF. Следовательно, эти треугольники имеют одинаковые по длине стороны. То есть сторона BF имеет ту же длину, что и сторона AF.
Если рассматривать треугольник AFB, то он будет равнобедренный (AF равняется BF), а прямая FC является медианой, так как по условиям построения сторона AC равняется стороне BC. Следовательно, угол ACF равняется 90 о . Что и следовало доказать.
Важным следствием из приведённой теоремы будет утверждение:
если две параллельные пересекают плоскость и одна из них составляет угол 90 о , то и вторая походит через плоскость под углом 90 о .
По условиям задачи a и b являются параллельными. Смотреть рисунок 4. Линия a перпендикулярна поверхности α. Отсюда следует, что линия b будет также перпендикулярна поверхности α.
Для доказательства через две точки пересечения параллельных прямых с плоскостью проведём на поверхности прямую c. По теореме о прямой, перпендикулярной плоскости, угол DAB будет 90 о . Из свойств параллельных прямых следует, что угол ABF тоже будет 90 о . Следовательно, по определению прямая b будет перпендикулярна поверхности α.
Использование теоремы для решения задач
Для закрепления материала, используя основополагающие условия перпендикулярности прямой и плоскости, решим несколько задач.
Задача № 1
Условия. Из точки A построить перпендикулярную линию плоскости α. Смотреть рисунок 5.
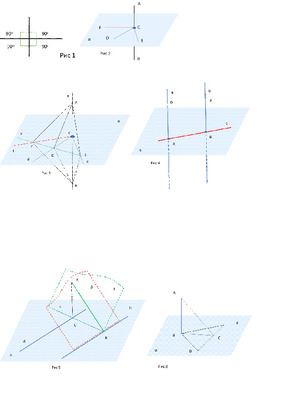
На поверхности α проведём произвольную прямую b. Через прямую b и точку A построим поверхность β. Из точки A на линию b проведём отрезок AB. Из точки B на поверхности α проведём перпендикулярную линию c.
Из точки A на линию с опустим перпендикуляр AC. Докажем, что эта линия будет перпендикулярна плоскости.
Для доказательства через точку C на поверхности α проведём линиюd, параллельную b, и через линию c и точку A построим плоскость. Линия AC перпендикулярна линии c по условию построения и перпендикулярна линии d, как следствие о двух параллельных линиях из теоремы о перпендикулярности, так как по условию линияb перпендикулярна поверхности γ.
Следовательно, по определению перпендикулярности линии и плоскости, построенный отрезок AC перпендикулярен поверхности α.
Задача № 2
Условия. Отрезок АВ перпендикулярен плоскости α. Треугольник BDF расположен на поверхности α и имеет следующие параметры:
- угол DBF будет 90 о
- сторона BD=12 см;
- сторона BF =16 см;
- BC — медиана.
Смотреть рисунок 6.
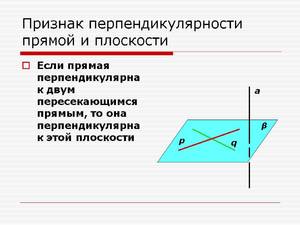
Найти длину отрезка АС, если АВ = 24 см.
Решение. По теореме Пифагора, гипотенуза или сторона DF равна квадратному корню из суммы квадратов катетов. Длина BD в квадрате равна 144 и, соответственно, BC в квадрате будет 256. В сумме 400; извлекая квадратный корень, получаем 20.
Медиана BC в прямоугольном треугольнике делит гипотенузу на две равные части и по длине равна этим отрезкам, то есть ВС = DC = CF = 10.
Снова используется теорема Пифагора, и получаем: гипотенуза C = 26, что является квадратным корнем из 675, суммы квадратов катетов 576 (АВ = 24 в квадрате) и 100 (ВС = 10 в квадрате).
Ответ: Длина отрезка АС равняется 26 см. C истема отсчета читайте в нашей статье.
Решение задач на перпендикулярность прямой и плоскости – урок 2 – ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ – ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Дополнительную задачу проверить индивидуально у нескольких учеников.
Дано: ABCD квадрат; AM – прямая; АМ ⊥ (ABCD); АС ∩ BD = О (рис. 1).
Доказать: a) BD ⊥ (АМО); б) МО ⊥ BD.
1) Так как МА ⊥ (ABCD), то МА ⊥ BD (по определению прямой, перпендикулярной плоскости). BD ⊥ AC (по свойству диагоналей квадрата). МА ⊂ (МАО) и АС ⊂ (МАО), МА ∩ АС = А. Следовательно, BD ⊥ (MAO) (по признаку перпендикулярности прямой и плоскости).
2) Так как BD ⊥ (МАО), то BD ⊥ МО, МО ⊂ (МАО) (по определению прямой, перпендикулярной плоскости).
Дано: АВ – отрезок; α; АВ ⊥ α; О – середина АВ, О ∈ α; ХА = ХВ. (рис. 2).
1) Если X ∈ АВ, то Х = О, и поэтому X ∈ а.
2) Если X ∉ АВ, то ХО – медиана ΔАХВ. ΔАХВ – равнобедренный (по определению), значит, ХО – высота (по свойству медианы равнобедренного треугольника), то есть ХО ⊥ АВ. Таким образом, О ∈ ХО, О ∈ АВ и ХО ⊥ АВ, следовательно, ХО ⊂ а (по задаче № 134) и X ∈ а.
Дано: ΔАВС; АВ = АС = ВС; CD ⊥ (ABC); AM = MB, DM = 15, CD = 12 (рис. 3).
1) CD ⊥ (ABC) ⇒ CD ⊥ AC и CD ⊥ ВС, тo есть ∠ACD = ∠BCD = 90° и ΔADC, ΔBDC -прямоугольные.
2) ΔADC = ΔBDC (по двум катетам): DC – общий, AC = ВС (по условию). Значит, AD = BD (как соответствующие в равных треугольниках), тогда ΔADB – равнобедренный (по определению) и DM – медиана. Следовательно, DM – высота (по свойству медианы равнобедренного треугольника).

3) DC ⊥ МС ⇒ ∠DCM = 90° и ΔMCD – прямоугольный. По теореме Пифагора: MD2 = DC2 + МС2. Тогда
4) ΔМСВ – прямоугольный (∠CMB = 90°, так как СМ – медиана и высота в ΔАВС – равностороннем), тогда (по условию),

5) (Ответ: 45√3.)
2. Решить самостоятельно задачу (выполняют учащиеся, у которых нет вопросов по домашнему заданию).
Дан тетраэдр МАВС, угольный, где D ∈ AC, MB ⊥ АВ. Найдите MD и SMBD, если MB = BD = а.
Дано: МАВС – тетраэдр; MB ⊥ АВ, MB ⊥ ВС; D ∈ AC, MB = BD = а (рис. 4).
Доказать: ΔMBD – прямоугольный.
Решение: Так как то MB ⊥ (ABC) (по признаку перпендикулярности прямой и плоскости).

Значит, (по определению прямой, перпендикулярной плоскости), то есть ∠MBD = 90°, а значит, ΔMBD – прямоугольный.
2) ΔMBD, по теореме Пифагора:
3) (Ответ: )
III. Математический диктант
Ответы записать на листочек и в тетрадь.
Листочек сдается на проверку учителю, а тетрадь остается для самопроверки, которая будет проведена непосредственно по окончанию работы.
1. Закончите предложение, чтобы получилось верное утверждение. Сделайте рисунок.
1.1. Две прямые называются перпендикулярными, если.
1.2. Если плоскость перпендикулярна одной из двух параллельных прямых, то она.
1.3. Если две плоскости перпендикулярны прямой, то они.
1.1. Прямая называется перпендикулярной к плоскости, если.
1.2. Две прямые, перпендикулярные одной и той же плоскости.
1.3. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая.
2. Ответьте на вопрос
2.1. Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости?
2.1. Сколько перпендикуляров можно провести через данную точку к данной прямой в пространстве?

3.1. Ребра, перпендикулярные плоскости (DCC1).
3.2. Плоскости, перпендикулярные ребру ВВ1.
3.1. Ребра, перпендикулярные плоскости (АВВ1).
3.2. Плоскости, перпендикулярные ребру A1D1.
4. Используя символы || и ⊥ запишите, как расположены прямая и плоскость (по рис. 5 из п. 3). Докажите.
5. АВ ⊥ α, CD ⊥ α, B ∈ α, D ∈ α, АВ = CD.
Каково взаимное положение прямой АС и плоскости α? Ответ обоснуйте.
5. AB ⊥ α, CD || АВ (В ∈ α, D ∈ α), Е ∈ α, ∠ECD = 40°. Тогда чему равны ∠CED? Ответ обоснуйте.
Ответы к заданиям математического диктанта
1.1. Угол между ними равен 90°.
1.2. Перпендикулярна и другой.
3.1. AD, A1D1, ВС, В1С1.
3.2. АВС и А1В1С1.
1.1. Она перпендикулярна к любой прямой, лежащей в этой плоскости.
1.3. Перпендикулярна плоскости.
3.1. AD1A1D1, BC1B1C1.
3.2. АА1В1 и DD1C1.
С самопроверкой по подготовленному решению задач.
№ 1. Основанием прямоугольного параллелепипеда является квадрат со стороной, равной а. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно. (рис. 6).
Найти: ρ (АА1; B1D).
1) (по признаку параллельности прямой и плоскости);

2) Так как ABCD – квадрат, то AC ⊥ BD, то есть
3) (Ответ: )
№ 2. ABCD – квадрат (рис. 7). АЕ – перпендикулярно плоскости квадрата, К ∈ BE. Чему равен угол между ВС и АК.

1) Так как ВС и АК – скрещивающиеся прямые, то ∠(ВС, АК) = ∠(АК; AD), т. к. ВС || AD (по свойству сторон квадрата).
2) AE ⊥ AD (по определению прямой, перпендикулярной плоскости), АВ ⊥ AD, т. к. ∠BAD = 90°, АЕ ∩ АВ = А, значит, AD ⊥ (АВЕ) (по признаку перпендикулярности прямой и плоскости).
3) Так как AD ⊥ (АВЕ), то AD ⊥ АК, АК ⊂ (АВЕ) (по определению прямой, перпендикулярной плоскости). Значит, ∠ (АК, АВ) = ∠KAD = 90°.
IV. Решение задач
Отрезок АВ пересекает некоторую плоскость в точке О. Прямые AD и ВС, перпендикулярные этой плоскости, пересекает ее в точках D и С соответственно. AD = 6 см, ВС = 2 см, ОС = 1,5 см. Найдите АВ.
Дано: α; АВ – отрезок; (рис. 8).

1. Так как

2. Так как тo
а) AD ⊥ DC и ВС ⊥ DC (по определению прямой, перпендикулярной плоскости). Значит, ∠ADC = ∠BCD = 90°;
б) AD || ВС (по теореме, обратной к теореме, о связи между параллельностью прямых и их перпендикулярностью к плоскости) и существует плоскость β: AD ⊂ β и ВС ⊂ β.
3. ΔADO и ΔВСО – прямоугольные, ∠ADC = ∠BCD = 90°. ∠A = ∠B (по свойству накрест лежащих углов, образованных параллельными прямыми AD и ВС и секущей АВ) ⇒ ΔADO ~ ΔВСО. Тогда (по определению подобных треугольников)

4. В ΔADO, по теореме Пифагора: АО = 7,5 см. В ΔВСО, по теореме Пифагора: BO2 = ВС2 + СО2, ВO2 = 4 + 2,25. ВO = 2,5 см.
5. АВ = АО + ОВ, АВ = 7,5 + 2,5 = 10 (см). (Ответ: 10 см.)
Задачу у доски, решает один ученик. Остальные учащиеся записывают решение в тетрадь, исправляя и дополняя отвечающего (по необходимости).
Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают ее в точках В и D соответственно. Найдите AС, если АВ = 9, CD = 15, BD = 8.
(Следует сообщить учащимся, что в задаче возможны два варианта расположения точек А, С и плоскости.)
а) точки А и С лежат по одну сторону от плоскости (у доски работает один ученик, выполняет полное решение со всеми необходимыми обоснованиями);
б) точки А и С лежат по разные стороны от плоскости (у доски работает один ученик, самостоятельно выполняя решение. Можно составить только план решения).
а) Дано: (рис. 9).

1.

2. Так как то АВ ⊥ BD и CD ⊥ BD (по определению прямой, перпендикулярной плоскости).
3. Так как АВ ⊥ α и CD ⊥ α, то АВ || CD (по теореме, обратной к теореме о связи между параллельностью прямых и их перпендикулярностью к плоскости) и существует плоскость β: АВ ⊂ β и CD ⊂ β. Тогда ABCD – трапеция, прямоугольная. Пусть АК – высота трапеции, тогда АК ⊥ KD. ABDK – прямоугольник (по признаку – углы прямые); АВ = KD = 9, BD = АК = 8 (по свойству сторон прямоугольника).

4. ΔАКС – прямоугольный: КС = CD – KD, КС = 15 – 9 = 6. По теореме Пифагора: (Ответ: 10..
1-2 аналогично случаю а.

3. Так как ВО + OD = 8, то ВО = 3, DO = 5.


(Ответ: 8√10.)
Диагональ BD параллелограмма ABCD перпендикулярна плоскости α. Найдите периметр параллелограмма, если АВ = 7 см, точки А и С лежат в плоскости α.
Дано: α; ABCD – параллелограмм; (рис. 10).

1) Так как А ∈ α, С ∈ α, то (по определению прямой, перпендикулярной плоскости). Значит, ABCD – ромб (по признаку). Тогда АВ = ВС = CD = AD = 7 см (по определению ромба).
2) РABCD = 4 · 7 = 28 (см). (Ответ: 28 см.)
V. Подведение итогов
1) Повторить теоретический материал по изученной теме.
2) Решить задачи № 131, дополнительные задачи:
1. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые HP и ME, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ, если HP = 4 см, НК = 5 см, ME = 12 см.
2. Треугольник ABC правильный, точка О – его центр. Прямая ОМ перпендикулярна плоскости ЛВС. Докажите, что МА = MB = МС. Найдите МА, если АВ = 6 см, МО = 2 см.
3. ABCD прямоугольник. Отрезок АЕ перпендикулярен к плоскости ABC. ЕВ = 15, ЕС = 24, ED = 20. Докажите, что треугольник EDC прямоугольный, и найдите АЕ.
4. Точка А принадлежит окружности, АК – перпендикуляр к ее плоскости, АК = 1 см, АВ – диаметр, ВС — хорда окружности, составляющая с АВ угол 45°. Радиус окружности равен 2 см. Докажите, что треугольник КСВ прямоугольный, и найдите КС.
I уровень – № 131, дополнительные задачи № 1, 2.
II уровень – № 131, дополнительные задачи № 3, 4.
Решение задач домашнего задания.
Дано: ABCD – тетраэдр; М ∈ ВС: ВМ = МС; АВ = AC, DB = DC (рис. 11).
Доказать: (ADM) ⊥ DC.
1. Так как АВ = АС, то ΔАВС – равнобедренный (по определению) и AM – медиана. Тогда AM – высота ΔАВС (по свойству медианы равнобедренного треугольника). Значит, AM ⊥ ВС.
2. Так как DB = DC, то ΔBCD – равнобедренный и DM – медиана. Тогда DM – высота, а значит, DM ⊥ ВС.

3. или (ADM) ⊥ ВС (по признаку перпендикулярности прямой и плоскости).
Дано: α, МН – отрезок, НР = 4 см, НК = 5 см, ME = 12 см (рис. 12).

1)

2) (по определению прямой, перпендикулярной плоскости) и ME || ЯР (по теореме, обратной к теореме, о связи между параллельностью прямых и их перпендикулярностью к плоскости), тогда существует плоскость β: ME ⊂ β.
3) Так как ME ⊥ РЕ и HР ⊥ РЕ, то ∠МЕК = ∠HPK = 90°, а ΔМЕК и ΔНРК – прямоугольные.

4) ΔНРК; НК2 = HР2 + КР2 (по теореме Пифагора). КР2 = НК2 – HP2,
5) ∠EMK = ∠PHK (по свойству накрест лежащих углов, образованных параллельными прямыми ME и HР и секущей МН). Тогда ΔМЕК ~ ΔНРК и (по определению подобных треугольников);
6) РЕ = РК + КЕ, РЕ = 3 + 9 = 12 (см). (Ответ: 12 см..
Дано: ΔАВС, АВ = ВС = АС; О – центр ΔАВС; ОМ ⊥ (ABC); АВ = 6 см, МО = 2 см (рис. 13).
Доказать: МА = MB = МС.
1) Так как О – центр ΔАВС, то АО = ВО = СО = R.
2) Так как МО ⊥ (ABC), то МО ⊥ АО, МО ⊥ ВО, МО ⊥ СО (по определению прямой, перпендикулярной плоскости). Тогда ∠MOA = ∠MOB = ∠MOC = 90°, а ΔМАО, ΔМВО и ΔМСО – прямоугольные.
3) ΔМАО = ΔМВО = ΔМСО (по двум катетам): МО – общий, АО = ВО = СО. Следовательно, МА = MB = МС.
4) По теореме Пифагора: (Ответ: 4 см.)
Дано: ABCD – прямоугольник; АЕ ⊥ (ABC); ЕВ = 15, ЕС = 24, ED = 20 (рис. 14).
Доказать: ΔEDC – прямоугольный.
1) Так как АЕ ⊥ (АВС), то AE ⊥ AD (по определению прямой, перпендикулярной плоскости). Значит, ∠DAE = ∠CAE = ∠BAE = 90°, a ΔDAE, ΔCAE, ΔBAE – прямоугольные.

2) ΔDAC – прямоугольный, ∠D = 90°, так как ABCD – прямоугольник. По теореме Пифагора: (DC = АВ – по свойству сторон прямоугольника).
3) По теореме Пифагора в ΔDAE: в ΔСАЕ: в ΔВАЕ: подставим (1) и (3) в (2), получим.




4) Значит, ∠CDE = 90° и ΔEDC – прямоугольный.
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
Перпендикулярность прямой и плоскости (ЕГЭ 2022)
Давай для полного понимания рассмотрим не только перпендикулярность прямой и плоскости, а все три случая перпендикулярности в пространстве.
Все относящиеся к ним определения и формулировки теорем.
А потом обсудим очень важную теорему о трёх перпендикулярах.
И ты будешь знать о перпендикулярности в пространстве все!
Поехали!
Перпендикулярность в пространстве — коротко о главном
Перпендикулярность двух прямых
Две прямые в пространстве перпендикулярны, если угол между ними ( 90<>^circ ).
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.
Перпендикулярность плоскостей
Плоскости перпендикулярны, если двугранный угол между ними равен ( 90<>^circ ).
Критерий перпендикулярности плоскостей
Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.
Теорема о трех перпендикулярах
Прямая ( a), не лежащая в плоскости ( alpha ), перпендикулярна прямой ( b), лежащей в плоскости ( alpha ), тогда и только тогда, когда проекция ( aprime ) прямой a перпендикулярна прямой ( b).
![]()
Перпендикулярность двух прямых
Определение:
Две прямые в пространстве перпендикулярны, если угол между ними ( displaystyle 90<>^circ ).
Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.
На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):
![]()
А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:
![]()
Прямая ( displaystyle a) перпендикулярна прямой ( displaystyle b), хотя и не пересекается с нею. Как так?
Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми ( displaystyle a) и ( displaystyle b), нужно через произвольную точку ( displaystyle O) на прямой a провести прямую ( displaystyle ’parallel b).
И тогда угол между ( displaystyle a) и ( displaystyle b) (по определению!) будет равен углу между ( displaystyle a) и ( displaystyle ’>).
Вспомнили? Ну вот, а в нашем случае – если окажутся перпендикулярны прямые ( displaystyle a) и ( displaystyle ’>), то нужно считать перпендикулярными прямые ( displaystyle a) и ( displaystyle b).
Для полной ясности давай рассмотрим пример
Эти прямые не пересекаются – они скрещиваются. Чтобы найти угол между ( displaystyle AC) и ( displaystyle _>_>), проведём ( displaystyle BD).
![]()
Из-за того, что ( displaystyle B_>_>D) — параллелограмм (и даже прямоугольник!), получается, что ( displaystyle _>_>parallel BD).
А из-за того, что ( displaystyle ABCD) – квадрат, выходит, что ( displaystyle ACbot BD). Ну, и значит ( displaystyle ACbot _>_>).
Перпендикулярность прямой и плоскости
Определение:
Прямая перпендикулярна плоскости , если она перпендикулярна всем прямым в этой плоскости.
![]()
Прямая ( displaystyle h) перпендикулярна плоскости ( displaystyle alpha ), если она перпендикулярна всем-всем прямым в этой плоскости: и ( displaystyle a), и ( displaystyle b), и ( displaystyle c), и даже ( displaystyle d)!
И ещё миллиарду других прямых!
Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит!
Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Оцени, как здорово:
![]()
Если найдутся всего лишь две пересекающиеся прямые (( displaystyle a) и ( displaystyle b)) в плоскости ( displaystylealpha), которым перпендикулярна прямая ( displaystyle h), то эта прямая сразу окажется перпендикулярна плоскости ( displaystyle alpha ),
То есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой ( displaystyle c)).
Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.
![]()
Что это за арка? Это значок «пересечение»! Хороший способ быстрее писать конспекты 🙂
Прямая перпендикулярна двум пересекающимся прямым!
И опять рассмотрим пример
Пусть нам дан правильный тетраэдр ( displaystyle ABCD).
![]()
Задача: доказать, что ( displaystyle BDbot AC).
Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!
![]()
Давай отметим середину ( displaystyle M) ребра ( displaystyle AC) и проведём ( displaystyle BM) и ( displaystyle DM).
Это медианы в ( displaystyle Delta ABC) и ( displaystyle Delta ADC).
Треугольники – правильные ( displaystyle Rightarrow BMbot AC) и ( displaystyle DMbot AC).
Вот оно, чудо: получается, что ( displaystyle ACbot BMD), так как ( displaystyle ACbot BM) и ( displaystyle ACbot DM).
И далее, ( displaystyle ACbot BMDRightarrow ACbot ) всем прямым в плоскости ( displaystyle BMD), а значит, и ( displaystyle ACbot BD).
И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.
Урок-исследование: “Признак перпендикулярности прямой и плоскости”
методическая разработка по геометрии (10 класс) на тему
Цель урока : Показать множественность подходов к доказательству теоремы; совершенствовать исследовательские умения и навыки учащихся.
Подготовка к уроку : ученики-консультанты дома готовят по дополнительной литературе семь доказательств признака перпендикулярности прямой и плоскости.
Вступительное слово учителя:
Сегодняшний урок – урок исследования. Всем вместе предстоит в процессе решения задач и ответов на проблемные вопросы, подойти к формулировке теоремы перпендикулярности прямой и плоскости и познакомиться с семью вариантами доказательств этой теоремы с тем, чтобы выбрать наиболее оптимальный из них, обстоятельно мотивировать своё мнение.
1.Подготовка к формулировке теоремы:
Повторение определения перпендикуляра к плоскости, анализ практического применения данного понятия посредством решения задач.
Даны: Плоскость , точки А и В в этой плоскости; АМ – прямая перпендикулярная этой плоскости. Определить вид треугольника АМВ.
Задачи по вариантам.
Дан плоский четырёхугольник АВСD. АМ – перпендикуляр к плоскости ABCD. Какие из треугольников ABC, ACD, ABD, BCD, ADM, ABM, CAM – прямоугольные.
ABCD – квадрат. Прямая ВК перпендикулярна плоскости квадрата. Какие из треугольников ABD, BCD, ABK, BDK, BCK – прямоугольные.
Консультанты собирают листочки и проверяют решения, а учитель подводит учащихся к выводу:
1.Верно ли утверждение, что прямая, перпендикулярная к плоскости,
перпендикулярна любой прямой лежащей в этой плоскости?
2.Когда же прямая перпендикулярна плоскости?
3.Сколько прямых лежат на плоскости? Можно ли их посчитать?
Далее учитель создаёт проблемную ситуацию, в основе которой – поиск ответа на вопрос: Сколько прямых достаточно в плоскости, чтобы можно было сказать, что прямая перпендикулярна плоскости?
Ученик – консультант на модели из спиц показывает различные варианты: в плоскости две прямые в плоскости, прямая перпендикулярна одной из них. Вывод: прямая не перпендикулярна плоскости. Следующий вариант модели: прямая перпендикулярна двум прямым, лежащим в плоскости, и, оказывается, перпендикулярна плоскости. Далее для закрепления, можно взять модель из трёх прямых и т. д.
По завершению работы с моделями перед учащимися ставится очередной проблемный вопрос: сколько прямых достаточно в плоскости, чтобы сказать, что прямая перпендикулярна плоскости?
Исследовав ситуацию перпендикулярности прямой и плоскости, мы в плотную подошли к теореме, которая даст возможность выяснить на чертежах, на моделях и в практика перпендикулярность к прямой и плоскости. Попробуем сформулировать теорему.
Ребята предлагают свои варианты формулировки теоремы. Учитель выделяет наиболее рациональнее и предлагает прослушать различные варианты формулировки и доказательства рассматриваемой теоремы, которые ученик разыскали дома в рекомендованной литературе.
2. Доказательство теоремы:
I вариант автор А.П. Киселев
Теорема: Если прямая, пересекающаяся с плоскостью, перпендикулярна каким – нибудь двум прямым, проведённым на этой плоскости через точку пересечения данной прямой и плоскости, то она перпендикулярна и ко всякой третьей прямой проведённой в этой плоскости через ту же точку пересечения.
Доказательство: Отложим на прямой AA 1 произвольной длины, но равные отрезки OA и OA 1 и проведём на плоскости какую-нибудь прямую, которая пересекла бы три прямые исходящие из точки О в точках C, D, и B .Эти точки соединим с точками A и A 1 ; мы получим несколько треугольников.∆ACB= ∆A 1 CB, так как у них BC – общая, AC=A 1 C – как наклонные к прямой AA 1 , одинаково удаленые от основания О перпендикуляра ОС. По той же причине AB=A 1 B .Из равенства этих треугольников следует, что ∟ABC=∟A 1 BC.
∆ABD=∆A 1 BD по первому признаку равенства треугольников: BD – общая, AB=A 1 B по доказанному, ∟ABC= ∟A 1 BC .Из равенства этих треугольников следует, что AD=A 1 D.
∆АОD=∆A1OD по третьему признаку равенства треугольников. Из равенства этих треугольников следует, что AOD= A1OD; и так как эти углы смежные, то AA1 перпендикулярна OD.
II вариант. Автор М.И.Башмаков
Теорема: Прямая, перпендикулярная двум пересекающимся прямым, принадлежащим плоскости, перпендикулярна плоскости.
Первый случай, когда все прямые a, b, c проходят через точку О – точку пересечения прямой с плоскостью α. Отметим на прямой р вектор OP, на прямой с вектор OC и докажем, что произведение векторов OP и OC равно 0.
Разложим вектор OC по векторам OA и OB, расположенные соответственно на прямых a и b; тогда (речь идет о векторах) OC=OA+OB. Значит:
Но OP ┴ OA, OP ┴ OB; поэтому OP∙OA=0, OP∙OB=0. Отсюда OP∙OC=0; значит OP ┴ OC и р ┴ с. Но с – любая прямая плоскости; значит, р ┴ α
Второй случай , когда прямые a, b, c не проходят через точку О. Проведем через точку О прямые a1||a; b1||b; c1||c. По условию p ┴ а, p ┴ b, значит p ┴ а1, p ┴ b1, и, по доказанному выше, p ┴ с1, а поэтому p ┴ с. Прямая с – любая прямая плоскости α; значит прямая р перпендикулярна ко всем прямым, лежащим в плоскости α, а поэтому p ┴ α.
III вариант. Автор А. В. Погорелов.
Теорема: Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
Перпендикулярные прямая и плоскость, признак и условия перпендикулярности прямой и плоскости
Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве. Все будет показано на примерах.
Перпендикулярные прямая и плоскость – основные сведения
Прямая перпендикулярна к плоскости, когда она перпендикулярна к любой прямой, лежащей в этой плоскости.
Верно то, что и плоскость перпендикулярна к прямой, как и прямая к плоскости.
Перпендикулярность обозначается « ⊥ ». Если в условии задано, что прямая с перпендикулярна плоскости γ , тогда запись имеет вид с ⊥ γ .
Например, если прямая перпендикулярна к плоскости, тогда возможно провести только одну прямую, благодаря которой две смежных стены комнаты пересекутся. Прямая считается перпендикулярной к плоскости потолка. Канат, расположенный в спортзале рассматривается в качестве отрезка прямой, который перпендикулярен плоскости, в данном случае полу.
При наличии перпендикулярной прямой к плоскости, угол между прямой и плоскостью считается прямым, то есть равен 90 градусов.
Перпендикулярность прямой и плоскости – признак и условия перпендикулярности
Для нахождения выявления перпендикулярности необходимо использовать достаточное условие перпендикулярности прямой и плоскости. Оно гарантирует выполнение перпендикулярности прямой и плоскости. Данное условие считается достаточным и называют признаком перпендикулярности прямой и плоскости.
Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, которые лежат в этой плоскости.
Подробное доказательство приведено в учебнике геометрии 10 – 11 класса. Теорема применяется для решения задач, где необходимо установить перпендикулярность прямой и плоскости.
При условии параллельности хоть одной из прямых плоскости, считается, что вторая прямая также перпендикулярна к данной плоскости.
Признак перпендикулярности прямой и плоскости рассматривается еще со школы, когда необходимо решить задачи по геометрии. Рассмотрим подробнее еще одно необходимое и достаточное условие, при котором прямая и плоскость будут перпендикулярны.
Для того, чтобы прямая а была перпендикулярна плоскости γ , необходимым и достаточным условием является коллинеарность направляющего вектора прямой а и нормального вектора плоскости γ .
При a → = ( a x , a y , a z ) являющимся вектором прямой a , при n → = ( n x , n y , n z ) являющимся нормальным вектором плоскости γ для выполнения перпендикулярности нужно, чтобы прямая a и плоскость γ принадлежали выполняемости условия коллинеарности векторов a → = ( a x , a y , a z ) и n → = ( n x , n y , n z ) . Отсюда получаем, что a → = t · n → ⇔ a x = t · n x a y = t · n y a z = t · n z , t является действительным числом.
Данное доказательство основывается на необходимом и достаточном условии перпендикулярности прямой и плоскости, направляющего вектора прямой и нормального вектора плоскости.
Данное условие применимо для доказательства перпендикулярности прямой и плоскости, так как достаточно найти координаты направляющего вектора прямой и координаты нормального вектора в трехмерном пространстве, после чего производить вычисления. Используется для случаев, когда прямая определена уравнением прямой в пространстве, а плоскость уравнением плоскости некоторого вида.
Доказать перпендикулярность заданной прямой x 2 – 1 = y – 1 2 = z + 2 2 – 7 с плоскостью x + 2 2 + 1 y – ( 5 + 6 2 ) z .
Знаменатели канонических уравнений являются координатами направляющего вектора данной прямой. Отсюда имеем, что a → = ( 2 – 1 , 2 , 2 – 7 ) является направляющим вектором прямой x 2 – 1 = y – 1 2 = z + 2 2 – 7 .
В общем уравнении плоскости коэффициенты перед переменными x , y , z являются координатами нормального вектора данной плоскости. Отсюда следует, что n → = ( 1 , 2 ( 2 + 1 ) , – ( 5 + 6 2 ) ) – это нормальный вектор плоскости x + 2 2 + 1 y – ( 5 + 6 2 ) z – 4 = 0
Необходимо произвести проверку выполнимости условия. Получаем, что
2 – 1 = t · 1 2 = t · 2 ( 2 + 1 ) 2 = t · ( – ( 5 + 6 2 ) ) ⇔ t = 2 – 1 , тогда векторы a → и n → связаны выражением a → = ( 2 – 1 ) · n → .
Это и есть коллинеарность векторов. отсюда следует, что прямая x 2 – 1 = y – 1 2 = z + 2 2 – 7 перпендикулярна плоскости x + 2 ( 2 + 1 ) y – ( 5 + 6 2 ) z – 4 = 0 .
Ответ: прямая и плоскость перпендикулярны.
Определить, перпендикулярны ли прямая y – 1 = 0 x + 4 z – 2 = 0 и плоскость x 1 2 + z – 1 2 = 1 .
Чтобы ответить на вопрос перпендикулярности, необходимо, чтобы было выполнено необходимое и достаточное условие, то есть для начала нужно найти вектор заданной прямой и нормальный вектор плоскости.
Из прямой y – 1 = 0 x + 4 z – 2 = 0 видно, что направляющий вектор a → – это произведение нормальных векторов плоскости y – 1 = 0 и x + 4 z – 2 = 0 .
Отсюда получаем, что a → = i → j → k → 0 1 0 1 0 4 = 4 · i → – k → .
Координаты вектора a → = ( 4 , 0 , – 1 ) .
Уравнение плоскости в отрезках x 1 2 + z – 1 2 = 1 является эквивалентным уравнению плоскости 2 x – 2 z – 1 = 0 , нормальный вектор которой равен n → = ( 2 , 0 , – 2 ) .
Следует произвести проверку на коллинеарность векторов a → = ( 4 , 0 , – 1 ) и n → = ( 2 , 0 , – 2 ) .
Для этого запишем:
4 = t · 2 0 = t · 0 – 1 = t · ( – 2 ) ⇔ t = 2 t ∈ R ⇔ t ∈ ∅ t = 1 2
Отсюда делаем вывод о том, что направляющий вектор прямой не коллинеарен нормальному вектору плоскости. Значит, y – 1 = 0 x + 4 z – 2 = 0 – это прямая, не перпендикулярная к плоскости x 1 2 + z – 1 2 .





